Rational function

red: graph of the fractional- rational function blue: pole line through the pole position with green: asymptote function , continuously correctable definition gap with ${\displaystyle f(x)={\tfrac {2(x+2)(x+1)(x-1)^{2}}{(x+1)(2x-1)}}}$
${\displaystyle x=0{,}5}$
${\displaystyle g(x)=x^{2}+x/2-11/4}$ ${\displaystyle x=-1}$

In mathematics, a rational function is a function that can be represented as the quotient of two polynomial functions . So it has the shape

${\displaystyle f(x)={\frac {a_{z}x^{z}+a_{z-1}x^{z-1}+\dotsb +a_{1}x+a_{0}}{b_{n}x^{n}+b_{n-1}x^{n-1}+\dotsb +b_{1}x+b_{0}}}={\frac {P_{z}(x)}{Q_{n}(x)}}}$

with natural numbers and . The numbers can be any real numbers (or complex numbers ); the only restriction is that it has to be. The highest coefficients and should not be zero. ${\displaystyle n}$ ${\displaystyle z}$ ${\displaystyle a_{z},\dotsc ,a_{0},b_{n},\dotsc ,b_{0}}$ ${\displaystyle Q_{n}\neq 0}$ ${\displaystyle a_{z}}$ ${\displaystyle b_{n}}$

In a more abstract way, one can allow elements of any body for the coefficients . The rational functions with complex coefficients belong to the meromorphic functions . ${\displaystyle a_{z},\dotsc ,a_{0},b_{n},\dotsc ,b_{0}}$

More generally, one can consider rational functions in several variables as well as rational functions on algebraic varieties over arbitrary fields.

Classification

• If the denominator polynomial is of degree , i.e. constant, one speaks of a completely rational function or of a polynomial function . ${\displaystyle Q_{n}}$ ${\displaystyle n=0}$
• If the function term can only be represented with a denominator polynomial of degree , then it is a fractional-rational function . ${\displaystyle n>0}$
  • If and , it is a really broken rational function . ${\displaystyle n>0}$ ${\displaystyle z<n}$
  • If and , then it is a question of an incorrectly broken rational function . It can be divided into a fully rational function and a genuinely fractional rational function using polynomial division (see below). ${\displaystyle n>0}$ ${\displaystyle z\geq n}$

Examples of rational functions with different numerator degrees and denominator degrees : ${\displaystyle z}$ ${\displaystyle n}$

example	alternative notation	z =	n =	Function type
${\displaystyle f\colon x\mapsto {\frac {3x^{3}-4x+5}{2}}}$	${\displaystyle f\colon x\mapsto {\frac {3}{2}}x^{3}-2x+{\frac {5}{2}}}$	3	0	completely rational
${\displaystyle f\colon x\mapsto {\frac {2x-1}{x^{2}+1}}}$		1	2	really broken rational
${\displaystyle f\colon x\mapsto {\frac {(x-1)^{2}\cdot (x+2)}{x\cdot (2-3x^{2})}}}$	${\displaystyle f\colon x\mapsto {\frac {x^{3}-3x+2}{2x-3x^{3}}}}$	3	3	fake broken rational
${\displaystyle f\colon x\mapsto x+1+{\frac {1}{x-1}}}$	${\displaystyle f\colon x\mapsto {\frac {x^{2}}{x-1}}}$	2	1	fake broken rational

Curve discussion

Using the functional term of the rational function , the following statements can be made about the function graph ( curve discussion ). ${\displaystyle f={p \over q}\colon x\mapsto {\frac {p(x)}{q(x)}}}$

Domain of definition, zeros and poles

The fractional rational function is not defined at the zeros of the denominator function . ${\displaystyle q}$

The zeros of a fractional-rational function are determined by those zeros of the counter function that belong to the domain of the entire function. ${\displaystyle p}$

A special case arises when a real number is the zero of the numerator polynomial and the denominator polynomial at the same time. Then numerator and denominator polynomials are divisible by the associated linear factor (possibly even several times), that is, the function term can be reduced with this factor (possibly several times). ${\displaystyle a\in \mathbb {R} }$ ${\displaystyle x-a}$

• If -time occurs more often in the denominator than in the numerator (with a natural number , ), then there is a pole ( then called the multiplicity of the pole); ${\displaystyle x-a}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n>0}$ ${\displaystyle n}$
• otherwise the rational function has a definition gap that can be continuously removed , and the function can be continued continuously ${\displaystyle a}$

Examples:

• The function has the domain because the denominator function the zero point has and the zero point , as this is the only zero of the counter function is (and to hear). is a (double) pole. ${\displaystyle f\colon x\mapsto {\frac {x-1}{(2x-4)^{2}}}}$ ${\displaystyle \mathbb {D} =\mathbb {R} \setminus \{2\}}$ ${\displaystyle q\colon x\mapsto (2x-4)^{2}}$ ${\displaystyle x=2}$ ${\displaystyle x=1}$ ${\displaystyle p\colon x\mapsto x-1}$ ${\displaystyle x=1}$ ${\displaystyle \mathbb {D} }$ ${\displaystyle x=2}$
• The function has the domain of definition . But now there is a zero of the numerator and denominator functions. In order to reduce the corresponding linear factor, the numerator and denominator are first factored (by factoring out or using the binomial formulas ); that leads to or after shortening . This results in: is a (simple) pole, on the other hand a continuously eliminable definition gap of , and has the zero (note: is not a zero of , because this value does not belong to !). The continuous continuation of results in: and . ${\displaystyle f\colon x\mapsto {\frac {x^{2}-x}{x^{2}-1}}}$ ${\displaystyle \mathbb {D} _{f}=\mathbb {R} \setminus \{\pm 1\}}$ ${\displaystyle x=1}$ ${\displaystyle (x-1)}$ ${\displaystyle f\colon x\mapsto {\frac {x\cdot (x-1)}{(x+1)\cdot (x-1)}}}$ ${\displaystyle f\colon x\mapsto {\frac {x}{x+1}}}$ ${\displaystyle x=-1}$ ${\displaystyle x=1}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle x=0}$ ${\displaystyle x=1}$ ${\displaystyle f}$ ${\displaystyle \mathbb {D} }$ ${\displaystyle f}$ ${\displaystyle {\tilde {f}}(x)={\frac {x}{x+1}}}$ ${\displaystyle \mathbb {D} _{\tilde {f}}=\mathbb {R} \setminus \{-1\}}$

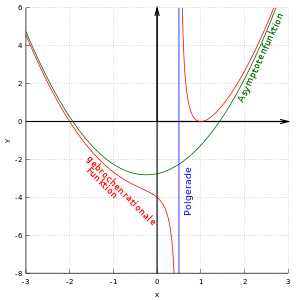
Asymptotic behavior

For the behavior towards infinity , the degrees or the numerator or denominator polynomial are decisive: ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle n}$

For goes ${\displaystyle x\to \infty }$ ${\displaystyle f(x)}$

• (Case 1) versus , if , where represents the sign function. ${\displaystyle \operatorname {sgn} \left({\tfrac {a_{z}}{b_{n}}}\right)\cdot \infty }$ ${\displaystyle z>n}$ ${\displaystyle \operatorname {sgn} }$
• (Case 2) against , if (the asymptote is parallel to the -axis), ${\displaystyle {\tfrac {a_{z}}{b_{n}}}}$ ${\displaystyle z=n}$ ${\displaystyle x}$
• (Case 3) against (the -axis is a horizontal asymptote), if , ${\displaystyle 0}$ ${\displaystyle x}$ ${\displaystyle z<n}$

For cases 2 and 3, the limit value is the same as for . In case 1, the numerator and denominator degrees have to be taken into account more precisely: ${\displaystyle x\to -\infty }$ ${\displaystyle x\to \infty }$

• Is even, the same limit results as for . ${\displaystyle z-n}$ ${\displaystyle x\to \infty }$
• If it is odd, the sign of the limit value changes compared to . ${\displaystyle z-n}$ ${\displaystyle x\to \infty }$

Examples:

• In the fractional- rational function is the numerator degree and the denominator degree , so the limit for is . ${\displaystyle f\colon x\mapsto {\frac {2x-1}{x^{2}+1}}}$ ${\displaystyle z=1}$ ${\displaystyle n=2}$ ${\displaystyle x\to \pm \infty }$ ${\displaystyle 0}$
• The fractional rational function has the numerator degree and also the denominator degree ; because here and is obtained for the equation of the horizontal asymptote: . ${\displaystyle f\colon x\mapsto {\frac {x^{3}-3x+2}{2x-3x^{3}}}}$ ${\displaystyle z=3}$ ${\displaystyle n=3}$ ${\displaystyle a_{3}=1}$ ${\displaystyle b_{3}=-3}$ ${\displaystyle y=-{\frac {1}{3}}}$
• The fractional rational function has the numerator degree and the denominator degree ; with the coefficients and thus results: for . Since it is odd here , it follows for the limit value for the reversed sign, that is . This function can also be written as , that is, the (oblique) asymptote has the equation (and the limit behavior just described can easily be derived from this). ${\displaystyle f\colon x\mapsto {\frac {x^{2}}{x-1}}}$ ${\displaystyle z=2}$ ${\displaystyle n=1}$ ${\displaystyle a_{2}=1}$ ${\displaystyle b_{1}=1}$ ${\displaystyle f(x)\to \operatorname {sgn} \left({\tfrac {1}{1}}\right)\cdot \infty =+\infty }$ ${\displaystyle x\to \infty }$ ${\displaystyle z-n=1}$ ${\displaystyle x\to -\infty }$ ${\displaystyle f(x)\to -\infty }$ ${\displaystyle f\colon x\mapsto x+1+{\frac {1}{x-1}}}$ ${\displaystyle y=x+1}$

Investigation with polynomial division

In case 1 ( ) mentioned above , the function term can be broken down into a sum of a polynomial and a truly fractional-rational term by means of polynomial division ; the polynomial then describes a so-called asymptote curve. The behavior of the function values ​​for described above can also be obtained more simply by examining only the behavior of this asymptotic curve. In a special case there is an inclined asymptote. ${\displaystyle z>n}$ ${\displaystyle x\to \pm \infty }$ ${\displaystyle z=n+1}$

As above, stand for the degree of the numerator polynomial and for the degree of the denominator polynomial . Again, all cases are considered (not only ). ${\displaystyle z}$ ${\displaystyle p(x)}$ ${\displaystyle n}$ ${\displaystyle q(x)}$ ${\displaystyle z>n}$

By means of a polynomial division of by one first receives a representation ${\displaystyle p(x)}$ ${\displaystyle q(x)}$

${\displaystyle p(x)=g(x)\cdot q(x)+r(x)}$

with polynomials and , where the degree of real is greater than that of . Hence the useful equation ${\displaystyle g(x)}$ ${\displaystyle r(x)}$ ${\displaystyle q(x)}$ ${\displaystyle r(x)}$

${\displaystyle f(x)={p(x) \over q(x)}=g(x)+{r(x) \over q(x)}}$.

The asymptotic behavior of is now the same asymptotic behavior of the completely rational function ("asymptote function ") . The quotient doesn't matter. ${\displaystyle f(x)}$ ${\displaystyle g(x)}$ ${\displaystyle r(x) \over q(x)}$

Once you've gone to the trouble of polynomial division and found the useful equation described above, it will be easier to distinguish between cases. The following applies:

Case 1: → -axis is asymptote: ${\displaystyle z<n}$ ${\displaystyle x}$ ${\displaystyle g(x)=0}$

Case 2: → horizontal asymptotes: ${\displaystyle z=n}$ ${\displaystyle g(x)={\frac {a_{z}}{b_{n}}}}$

Case 3: → oblique asymptote: with and ${\displaystyle z=n+1}$ ${\displaystyle g(x)=mx+c}$ ${\displaystyle m={\frac {a_{z}}{b_{n}}}}$ ${\displaystyle c={\frac {a_{z-1}}{b_{n}}}-{\frac {a_{z}b_{n-1}}{b_{n}^{2}}}}$

Case 4: → is a polynomial of degree ; the leading coefficient of this polynomial is the same . ${\displaystyle z>n+1}$ ${\displaystyle g(x)}$ ${\displaystyle z-n}$ ${\displaystyle {\frac {a_{z}}{b_{n}}}}$

symmetry

A polynomial function (completely rational function) is even / odd if all exponents are even / odd. If the numerator polynomial and denominator polynomial are of one of these two types, then the rational function is also even or odd: ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle f}$

• If and are both even or both odd, then is even (i.e. the graph is symmetric about the y-axis) ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle f}$
• If even and odd, then is odd (i.e. the graph is point symmetric about the origin); the same applies if is odd and even. ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle f}$ ${\displaystyle p}$ ${\displaystyle q}$

In all other cases, when the numerator or denominator function or both are neither even nor odd, symmetry properties are more difficult to decide. (See also Curve Discussion and Symmetry in Geometry ). ${\displaystyle f}$

Examples:

• The graph for the function with is symmetrical to the origin, since it is odd and even, so the function as a whole is odd. ${\displaystyle f}$ ${\displaystyle f(x)={\frac {2x^{3}-3x}{x^{2}+1}}}$ ${\displaystyle p}$ ${\displaystyle q}$
• The graph for the function is symmetrical to the y-axis, since and both are odd, so the function as a whole is even. You can also see it differently: If you take x from the numerator and denominator , you can shorten the functional term to ; now and are straight, the function as a whole is straight again. ${\displaystyle f\colon x\mapsto {\frac {x^{5}-x^{3}}{x^{3}+x}}}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle f(x)={\frac {x^{4}-x^{2}}{x^{2}+1}}}$ ${\displaystyle p}$ ${\displaystyle q}$
• In the graph of the function with the term , no symmetry can be recognized at first ( is odd, but neither even nor odd); but one can show that the graph is symmetric about the point P (1 | 1) ; namely: ${\displaystyle f(x)={\frac {x}{x-1}}}$ ${\displaystyle p}$ ${\displaystyle q}$

  ${\displaystyle f(1+x)-1={\frac {1+x}{(1+x)-1}}-1={\frac {1+x}{x}}-{\frac {x}{x}}={\frac {1}{x}}}$ and

  ${\displaystyle 1-f(1-x)=1-{\frac {1-x}{(1-x)-1}}={\frac {x}{x}}+{\frac {1-x}{x}}={\frac {1}{x}}}$,

so in total: what exactly symmetry to point P (1 | 1) means. Alternatively, one can also show that the graph of results from the graph of the function (which is symmetrical to the origin) by shifting it by 1 in the direction and by 1 in the direction. ${\displaystyle f(1+x)-1=1-f(1-x)}$ ${\displaystyle f}$ ${\displaystyle g\colon x\mapsto {\frac {1}{x}}}$ ${\displaystyle x}$ ${\displaystyle y}$

Derivation

To derive fractional rational functions one generally has to use the quotient rule ; in addition, the chain rule can often be useful, for example if the denominator function is a power of a binomial . Before deriving it, it is often advisable to first rewrite the function term with the help of a polynomial division and to shorten the remaining true fractional rational term.

Examples:

• With the function , it makes sense to use the chain rule in addition to the quotient rule instead of first using the first binomial formula in the denominator . With the chain rule, the derivation of the denominator function (usually referred to as in the quotient rule) results : ${\displaystyle f\colon x\mapsto {\frac {2x-1}{(x^{2}+1)^{2}}}}$ ${\displaystyle q}$ ${\displaystyle v}$

  ${\displaystyle q'(x)=2(x^{2}+1)\cdot 2x=4x(x^{2}+1)}$,

and thus overall for the derivative function of : ${\displaystyle f}$

${\displaystyle f'(x)={\frac {2\cdot (x^{2}+1)^{2}-(2x-1)\cdot 4x(x^{2}+1)}{(x^{2}+1)^{4}}}}$.

You can now exclude and reduce a factor in the numerator : ${\displaystyle (x^{2}+1)}$

${\displaystyle f'(x)={\frac {2\cdot (x^{2}+1)-(2x-1)\cdot 4x}{(x^{2}+1)^{3}}}}$.

Finally, simplify the numerator lists

${\displaystyle f'(x)={\frac {-6x^{2}+4x+2}{(x^{2}+1)^{3}}}}$.

• The function term is first given the form with the help of a polynomial division ${\displaystyle f(x)={\frac {x^{4}+x^{3}-7x^{2}-12x-4}{3x^{3}+12x^{2}+12x}}}$

  ${\displaystyle f(x)={\frac {1}{3}}x-1+{\frac {x^{2}-4}{3x^{3}+12x^{2}+12x}}}$,

from which you can read off the equation of the oblique asymptote:

${\displaystyle y={\frac {1}{3}}x-1}$.

Factoring the numerator and denominator then lists

${\displaystyle f(x)={\frac {1}{3}}x-1+{\frac {(x+2)(x-2)}{3x(x+2)^{2}}}}$,

so one can reduce a factor . After all, you have: ${\displaystyle (x+2)}$

${\displaystyle f(x)={\frac {1}{3}}x-1+{\frac {x-2}{3x^{2}+6x}}}$;

in this form one can derive the function much more easily than in the one originally given.

With the help of the quotient rule we get:

${\displaystyle f'(x)={\frac {1}{3}}+{\frac {1\cdot (3x^{2}+6x)-(x-2)\cdot (6x+6)}{(3x^{2}+6x)^{2}}}={\frac {1}{3}}+{\frac {-3x^{2}+12x+12}{(3x^{2}+6x)^{2}}}={\frac {1}{3}}+{\frac {-x^{2}+4x+4}{3x^{2}(x+2)^{2}}}}$.

If you set the first derivative equal to zero in order to look for the extreme points, it is advisable to combine the two fractions again beforehand:

${\displaystyle f'(x)={\frac {x^{2}(x+2)^{2}-x^{2}+4x+4}{3x^{2}(x+2)^{2}}}={\frac {x^{4}+4x^{3}+3x^{2}+4x+4}{3x^{2}(x+2)^{2}}}}$.

Indefinite integral

In contrast to the completely rational functions , it is often relatively difficult to find an antiderivative with fractional rational functions . Depending on the form of the fractional-rational function, the following rules can be used for this (usually you first have to bring the function term into a suitable form by transformations and / or substitutions ):

${\displaystyle \int {\frac {1}{mx+a}}dx={\frac {1}{m}}\cdot \ln(mx+a)+C}$ For ${\displaystyle m,a\in \mathbb {R} ,m\neq 0}$

${\displaystyle \int {\frac {1}{(mx+a)^{n}}}dx={\frac {1}{m}}\cdot {\frac {-1}{n-1}}\cdot {\frac {1}{(mx+a)^{n-1}}}+C}$ For ${\displaystyle m,a\in \mathbb {R} ,m\neq 0,n\in \mathbb {N} \setminus \{0;1\}}$

${\displaystyle \int {\frac {1}{x^{2}+1}}dx=\arctan(x)+C}$ or ${\displaystyle =-{\rm {arccot(x)+C}}}$

${\displaystyle \int {\frac {1}{x^{2}-1}}dx=\operatorname {artanh} (x)+C={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)}$ For ${\displaystyle |x|<1}$

${\displaystyle \int {\frac {1}{x^{2}-1}}dx=\operatorname {arcoth} (x)+C={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)}$ For ${\displaystyle |x|>1}$

${\displaystyle \int {\frac {u'(x)}{u(x)}}dx=\ln |u(x)|+C}$ For ${\displaystyle u(x)\neq 0}$

Partial fraction decomposition can often be helpful for determining an antiderivative . Examples:

• We are looking for an antiderivative to . Using a polynomial division, this can first be rewritten as: ${\displaystyle f(x)={\frac {5x-1}{3x+2}}}$

  ${\displaystyle f(x)={\frac {5}{3}}-{\frac {13}{9x+6}}}$.

Applying the first rule then yields the possible antiderivative:

${\displaystyle F(x)={\frac {5}{3}}x-{\frac {13}{9}}\ln(9x+6)}$.

• We are looking for an antiderivative to , where it should lie between −0.5 and 0.5. Again, the function term can first be rewritten using a polynomial division: ${\displaystyle f(x)={\frac {x^{2}+1}{x^{2}-1}}}$ ${\displaystyle x}$

  ${\displaystyle f(x)=1+{\frac {2}{x^{2}-1}}}$.

Applying the fourth rule then yields as a possible antiderivative:

${\displaystyle F(x)=x+2\cdot \operatorname {artanh} (x)}$.

• We are looking for an antiderivative to . That can also be written as ${\displaystyle f(x)={\frac {x+2}{x^{2}+4x+5}}}$

  ${\displaystyle f(x)={\frac {1}{2}}{\frac {2x+4}{x^{2}+4x+5}}={\frac {1}{2}}{\frac {u'(x)}{u(x)}}}$with . ${\displaystyle u(x)=x^{2}+4x+5}$

Applying the last rule then yields the possible antiderivative:

${\displaystyle F(x)={\frac {1}{2}}\ln(x^{2}+4x+5)}$.

• An antiderivative to can be determined with the help of the substitution , after the denominator has been transformed by adding the square : ${\displaystyle f(x)={\frac {1}{x^{2}+2x+2}}}$ ${\displaystyle y=x+1}$

  ${\displaystyle {\begin{aligned}\int {\frac {1}{x^{2}+2x+2}}dx&=\int {\frac {1}{(x+1)^{2}+1}}dx=\int {\frac {1}{y^{2}+1}}dy\\&=\arctan(y)+C=\arctan(x+1)+C\end{aligned}}}$

• An antiderivative to can be obtained with the help of the partial fraction decomposition, after having first factored the denominator: ${\displaystyle f(x)={\frac {1}{x^{2}-x-6}}}$

  ${\displaystyle {\begin{aligned}\int {\frac {1}{x^{2}-x-6}}dx&=\int {\frac {1}{(x-3)(x+2)}}dx=\int {\frac {1}{5}}\left({\frac {1}{x-3}}-{\frac {1}{x+2}}\right)dx\\&={\frac {1}{5}}\left(\ln(x-3)-\ln(x+2)\right)+C={\frac {1}{5}}\ln \left({\frac {x-3}{x+2}}\right)+C\end{aligned}}}$

Rational functions in several variables

A rational function in variables is a function of the form , where and are polynomials in the indeterminate and . ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle f(x_{1},\ldots ,x_{n})={\frac {P(x_{1},\ldots ,x_{n})}{Q(x_{1},\ldots ,x_{n})}}}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle Q\not =0}$

Examples

• ${\displaystyle f(x_{1},\ldots ,x_{n})={\frac {x_{1}^{2}+\ldots +x_{n}^{2}}{1-x_{1}\ldots x_{n}}}}$
• ${\displaystyle f(x,y)={\frac {xy}{x+y}}}$
• ${\displaystyle f(m,M)={\frac {m}{2M+m}}g}$

continuity

The definition range of consists of those points that are either not a zero of or whose multiplicity as a zero of is at least as large as the multiplicity of as a zero of . Rational functions are continuous in all points of their domain . ${\displaystyle f}$ ${\displaystyle (x_{1},\ldots ,x_{n})}$ ${\displaystyle Q}$ ${\displaystyle P}$ ${\displaystyle Q}$

Applications

Rational functions have a wide range of applications in science and technology:

• Many quantities are inversely proportional to one another, so one of the quantities is a rational function of the other, with the numerator being constant and the denominator a (homogeneous) linear function . A few examples:
  • The speed and the time required for a fixed distance are inversely proportional to each other: ${\displaystyle v}$ ${\displaystyle s}$ ${\displaystyle t}$ ${\displaystyle t(v)={\tfrac {s}{v}}}$
  • The concentration of a substance at a fixed amount of material is inversely proportional to the volume of the solvent: ${\displaystyle c}$ ${\displaystyle n}$ ${\displaystyle V}$ ${\displaystyle C(V)={\tfrac {n}{V}}}$
  • Acceleration and mass are at fixed force inversely proportional to one another . ${\displaystyle F}$ ${\displaystyle a(m)={\tfrac {F}{m}}}$
  • The following applies to the capacitance of a plate capacitor , depending on the plate spacing : with the area of the plates, the electrical field constant and the permittivity . ${\displaystyle C}$ ${\displaystyle d}$ ${\displaystyle C(d)=\epsilon _{0}\epsilon _{r}{\tfrac {A}{d}}}$ ${\displaystyle A}$ ${\displaystyle \epsilon _{0}}$ ${\displaystyle \epsilon _{r}}$
• In many areas of physics functions come from two variables and the following form: . Is one of the two variables, e.g. B. , constant or if you choose it as a parameter , then a rational function (or function family ) of . Such functions always occur when the total reciprocal of any quantity is the sum or difference of the reciprocal values ​​of two other functions. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle f(x;y)={\tfrac {xy}{x\pm y}}}$ ${\displaystyle y}$ ${\displaystyle x}$
  • By means of the lens equation of the optics can be the focal length as a function of object distance and image distance representing: ; switch to or deliver a very similar function, but with - instead of +. ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle b}$ ${\displaystyle f(g;b)={\tfrac {gb}{g+b}}}$ ${\displaystyle g}$ ${\displaystyle b}$
  • The total resistance of a parallel connection of two resistors and results in :; an analogous formula applies to the series connection of two capacitors . ${\displaystyle R}$ ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$ ${\displaystyle R={\tfrac {R_{1}R_{2}}{R_{1}+R_{2}}}}$
  • In the mechanics arises when two springs with spring constants and hangs together for the entire spring constant of the arrangement: ${\displaystyle D_{1}}$ ${\displaystyle D_{2}}$ ${\displaystyle D}$ ${\displaystyle D={\tfrac {D_{1}D_{2}}{D_{1}+D_{2}}}}$
• In the case of a voltage divider , the total voltage dropped across a resistor is given by :, where is the voltage to be divided and the other is resistance. ${\displaystyle R}$ ${\displaystyle U}$ ${\displaystyle U(R)={\tfrac {U_{0}R}{R+R'}}}$ ${\displaystyle U_{0}}$ ${\displaystyle R'}$
• For the electrical power that a device with a resistance that of a voltage source (voltage yields ) with internal resistance is connected, the result is: . The greatest possible performance (to be determined with the help of the differential calculation) is obtained when is ( performance adjustment ). ${\displaystyle P}$ ${\displaystyle R}$ ${\displaystyle U}$ ${\displaystyle R_{i}}$ ${\displaystyle P(R)={\tfrac {U^{2}R}{(R+R_{i})^{2}}}}$ ${\displaystyle R=R_{i}}$
• For the inductance (not too short) of a coil in dependence on its radius is true: . Here, the length of the coil (it is therefore also known as rational function of understand) the number of turns and the magnetic field constant . ${\displaystyle L}$ ${\displaystyle r}$ ${\displaystyle L(r)={\tfrac {\mu _{0}N^{2}\pi r^{2}}{l+r/1,1}}}$ ${\displaystyle l}$ ${\displaystyle L}$ ${\displaystyle l}$ ${\displaystyle N}$ ${\displaystyle \mu _{0}}$
• The braking force of an eddy current brake depends on the speed as follows: with constants and . ${\displaystyle B}$ ${\displaystyle v}$ ${\displaystyle B(v)={\tfrac {av}{b+v^{2}}}}$ ${\displaystyle a}$ ${\displaystyle b}$
• In the Atwood machine the acceleration depends on the two masses and as follows :; so one can understand both of and of as a rational function . ${\displaystyle a}$ ${\displaystyle m}$ ${\displaystyle M}$ ${\displaystyle a={\tfrac {m}{2M+m}}\cdot g}$ ${\displaystyle a}$ ${\displaystyle m}$ ${\displaystyle M}$
• Geometric questions also often lead to rational functions. For example, if a trunk consisting of a cuboid (base side lengths and , height ) with an attached semi- cylinder (height , radius is), applies to the surface area as a function of a given volume : . ${\displaystyle l}$ ${\displaystyle 2r}$ ${\displaystyle r}$ ${\displaystyle l}$ ${\displaystyle r}$ ${\displaystyle O}$ ${\displaystyle r}$ ${\displaystyle V}$ ${\displaystyle O(r)={\tfrac {(\pi +4)r^{3}+2V}{r}}}$

Different meaning in abstract algebra

Rational functions over any body

→ Main article : Rational function body

In abstract algebra , the term rational function is used in a more general and somewhat different sense. A rational function in variables over a body is understood to be an element of the quotient field of the polynomial ring . This quotient field is called a rational function field . ${\displaystyle n}$ ${\displaystyle X_{1},X_{2},\dotsc ,X_{n}}$ ${\displaystyle K}$ ${\displaystyle K\left[X_{1},X_{2},\dotsc ,X_{n}\right]}$

In general, a rational function is not a function of any kind, but a (formal) fraction of two polynomials. The converse does not have to apply, but the difference is only noticeable over finite fields: For example, for every prime number over the finite field (the field of all remainder classes of integers modulo ) the fraction is a well-defined rational function in the variable , but not a function in the actual sense of the term, because one cannot insert a single value in this function without the denominator becomes 0. (Because if you insert any into this "function", you get what is undefined, because the denominator is 0 according to Fermat's little theorem .) However, over infinite fields a rational function is always a function that may have a definition gap , but this definition gap is only very small compared to the domain of definition. This idea is formalized with the concept of the Zariski topology : The definition gap is a Zariski-closed set, and the closed shell of the domain is the whole set. ${\displaystyle p}$ ${\displaystyle \mathbb {F} _{p}}$ ${\displaystyle p}$ ${\displaystyle {\tfrac {1}{X^{p}-X}}}$ ${\displaystyle X}$ ${\displaystyle x\in \mathbb {F} _{p}}$ ${\displaystyle {\tfrac {1}{x^{p}-x}}}$ ${\displaystyle x^{p}-x}$

Rational functions on an algebraic variety

→ Main article : Rational function field # Function field in algebraic geometry

Let be an algebraic variety defined by polynomials , so ${\displaystyle V}$ ${\displaystyle f_{1},\dotsc ,f_{m}\in k\left[x_{1},\dotsc ,x_{n}\right]}$

${\displaystyle V=\{x\in \mathbb {A} ^{n}\mid f(x)=0{\text{ für alle }}f\in S\}.}$

Be

${\displaystyle I(V)=\{f\in k[x_{1},\dotsc ,x_{n}]\mid f(x)=0{\text{ für alle }}x\in V\}.}$

The ring of the whole features is . The body of the rational functions is the quotient body of the ring of all functions. ${\displaystyle k[x_{1},\dotsc ,x_{n}]/I(V)}$

More generally there is the term rational mappings between (quasi-projective) varieties. Rational functions are the special case of rational mappings from a variety to . ${\displaystyle \mathbb {A} ^{1}}$

Web links

Commons : Rational functions  - collection of pictures, videos and audio files

• Rational functions - A digital textbook © 2000 - 2001 by Henning Koch