Deterministic finite automaton

A deterministic finite automaton ( DEA ; English deterministic finite state machine or deterministic finite automaton , DFA ) is a finite automaton that by entering a character of its input alphabet (the possible inputs) from a state in which it is located to a uniquely determined The next state changes. From each (final) state there must be a transition to a subsequent state for each character of the input alphabet . In this it differs from nondeterministic finite automata , whose state change does not always have to occur deterministically . ${\displaystyle q_{n}\in \{F,Q\}}$ ${\displaystyle \Sigma }$

definition

Automat

Formally, a DEA can be defined as a quintuple (5-tuple) . The following applies here: ${\displaystyle {\mathfrak {A}}}$ ${\displaystyle {\mathfrak {A}}=\left(Q,\,\Sigma ,\,\delta ,\,q_{0},\,F\right)}$

• ${\displaystyle Q}$is a finite set of states . Other symbols often used for are or . ${\displaystyle Q}$ ${\displaystyle Z}$ ${\displaystyle S}$
• ${\displaystyle \Sigma }$is the finite input alphabet , i.e. the set of allowed input symbols.
• ${\displaystyle \delta \colon Q\times \Sigma \rightarrow Q}$is the transition function (or transition function ). It assigns a successor state to each pair consisting of a state and an input symbol . ${\displaystyle q\in Q}$ ${\displaystyle a\in \Sigma }$ ${\displaystyle p\in Q}$
• ${\displaystyle q_{0}\in Q}$is the start state (also initial state or initial state ).
• ${\displaystyle F\subseteq Q}$ is the set of accepting states, the so-called final states (or final states ). Another common symbol for is . ${\displaystyle F}$ ${\displaystyle A}$

behavior

If the machine is in one state and reads the input symbol , it changes to a new state that is specified by the transition function, i.e. into the state . ${\displaystyle {\mathfrak {A}}=\left(Q,\,\Sigma ,\,\delta ,\,q_{0},\,F\right)}$ ${\displaystyle q\in Q}$ ${\displaystyle a\in \Sigma }$ ${\displaystyle \delta (q,\,a)}$

If the machine has not yet read an input symbol, it is in the start state . If the machine receives a sequence of input symbols as input, called a word in theoretical computer science , it reads one symbol after the other from left to right and changes the state according to the transition function. If the machine is in an accepting state after reading the last input symbol , it accepts the input. One then says that the input word is in the set of words that are accepted by the automaton (in short: the language accepted by the automaton, see below). ${\displaystyle q_{0}}$ ${\displaystyle q_{f}\in F}$

Discarded entries

If the machine ends in a non-accepting state after reading an input word, the input is considered rejected. If the question of whether the input is rejected or accepted is not cleared up with the last input symbol, a minimal machine is prematurely in a state that it no longer leaves.

Language of a DEA

The set of all words accepted by the DEA is called the language of . The set of all languages ​​accepted by any DEA is the regular language class . ${\displaystyle {\mathfrak {A}}}$ ${\displaystyle {\mathcal {L}}({\mathfrak {A}})}$ ${\displaystyle {\mathfrak {A}}}$

Nondeterministic finite automata (NEA), DEA, and type 3 grammars (in the Chomsky hierarchy ) describe the same language class. NEA can be converted into equivalent DEA using power set construction .

Examples

Drinks machine

A deterministic finite machine that simulates the simple processes of a drinks machine can consist of the states that describe the following states of the drinks machine: "drinks machine waiting for a coin to be inserted", "drinks machine waiting for a drink to be selected" and "drink being served". ${\displaystyle Q=\{q_{0},q_{1},q_{2}\}}$

Valid input symbols could use the amount to describe the insertion of a coin, the selection of a drink, the cancellation of the drink selection and the removal of a drink. ${\displaystyle \Sigma =\{{\text{Münze}},{\text{Getränk}},{\text{Abbruch}},{\text{Entnahme}}\}}$

An automaton with the transitions

• ${\displaystyle \delta (q_{0},{\text{Münze}})=q_{1}}$,
• ${\displaystyle \delta (q_{1},{\text{Getränk}})=q_{2}}$,
• ${\displaystyle \delta (q_{2},{\text{Entnahme}})=q_{0}}$ and
• ${\displaystyle \delta (q_{1},{\text{Abbruch}})=q_{0}}$

then describes that payment is first made with a coin, then a drink is selected, which has to be removed before the user can start again. If you have inserted the coin but not yet selected a drink, you can also cancel.

If a complete function is required for the transitions, a state must be specified, among other things, into which the machine changes when it is canceled if a drink has already been selected but not yet removed.

• 

  Graphic representation of the DEA from the example

• 

  The corresponding DEA with a total transition function

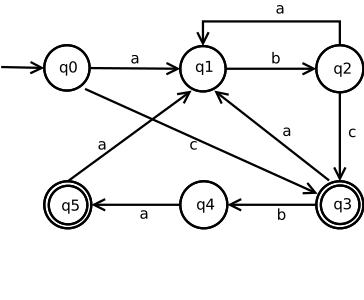
Regular expression

The regular expression can be represented as the following DEA: ${\displaystyle ((ab)^{*}c(ba\mid \varepsilon ))^{+}}$

• State quantity ${\displaystyle Q=\{q_{0},q_{1},q_{2},q_{3},q_{4},q_{5}\}}$
• Input alphabet ${\displaystyle \Sigma =\{a,b,c\}}$
• partial transition function with ${\displaystyle \delta \colon Q\times \Sigma \rightarrow Q}$
  • ${\displaystyle \delta (q_{0},a)=q_{1}}$
  • ${\displaystyle \delta (q_{0},c)=q_{3}}$
  • ${\displaystyle \delta (q_{1},b)=q_{2}}$
  • ${\displaystyle \delta (q_{2},a)=q_{1}}$
  • ${\displaystyle \delta (q_{2},c)=q_{3}}$
  • ${\displaystyle \delta (q_{3},a)=q_{1}}$
  • ${\displaystyle \delta (q_{3},b)=q_{4}}$
  • ${\displaystyle \delta (q_{4},a)=q_{5}}$
  • ${\displaystyle \delta (q_{5},a)=q_{1}}$
• Final states ${\displaystyle F=\{q_{3},q_{5}\}}$

• 

  Graphic representation of the DEA from the example

Minimization

For each DEA ​​there is a unique minimal automaton (apart from the naming of the states) that accepts the same language.

Since the states of the minimal automaton correspond to the equivalence classes of the language accepted by the finite automaton under the Nerode relation , one also speaks of the equivalence class automaton : ${\displaystyle {\mathfrak {A}}}$

${\displaystyle u\sim _{L({\mathfrak {A}})}v\Longleftrightarrow (\forall w\in \Sigma ^{*}:uw\in L({\mathfrak {A}})\Leftrightarrow vw\in L({\mathfrak {A}}))}$

Let be a deterministic finite automaton. Then is with ${\displaystyle {\mathfrak {A}}=(Q,\Sigma ,\delta ,q_{0},F)}$ ${\displaystyle {\mathfrak {B}}=(Q',\Sigma ,\delta ',q_{0}',F')}$

• ${\displaystyle Q'={\Big \{}[w]_{L({\mathfrak {A}})}\mid w\in \Sigma ^{*}{\Big \}}}$
• ${\displaystyle ~q'_{0}=[\epsilon ]_{L({\mathfrak {A}})}}$
• ${\displaystyle ~\delta '([u]_{L({\mathfrak {A}})},a)=[ua]_{L({\mathfrak {A}})}}$
• ${\displaystyle F'={\Big \{}[u]_{L({\mathfrak {A}})}\mid u\in L({\mathfrak {A}}){\Big \}}}$

the equivalence class automaton too . ${\displaystyle {\mathfrak {A}}}$

The minimization of a deterministic automaton can be solved algorithmically by continually refining the equivalence classes. You start with the state sets and . For each letter from the alphabet, each set of states is now divided in such a way that the transfer function maps the states of each new set of the letter into a unique set. This is repeated until there is no more change. ${\displaystyle F}$ ${\displaystyle Q-F}$

There is also the possibility of constructing minimal deterministic finite automata incrementally. Incremental here means that the words to be accepted are added individually to the machine. Every time such a word is inserted, the deterministic finite automaton is minimal. This method is particularly promising if the words often share common prefixes and suffixes, e.g. This is the case, for example, with words from natural languages.

See also

• Two-way DFA
• Power automaton
• Unique finite automaton

literature

• John E. Hopcroft , Rajeev Motwani , Jeffrey D. Ullman : Introduction to Automata Theory, Formal Languages, and Complexity Theory. 2nd Edition. Pearson Studies, Reading 2002, ISBN 3-8273-7020-5
• Gottfried Vossen, Kurt Ulrich Witt : Basic course in theoretical computer science . 3. Edition. ISBN 3-528-23147-5
• Peter Sander, Wolffried Stucky, Rudolf Herschel: Automata, Languages, Predictability . Teubner, Stuttgart 1992, ISBN 3-519-02937-5
• Uwe Schöning : Ideas in computer science, basic models and concepts . Oldenbourg, Munich 2006, ISBN 3-486-57833-2
• Jan Daciuk, Bruce W. Watson, Richard E. Watson, Ul. G. Narutowicza: Incremental Construction of Minimal Acyclic Finite State Automata and Transducers . 1998.

Web links

• Automaton Simulator - a web-based, graphical editor and simulator (English)

Individual evidence

1. ^ Hans Werner Lang, Hochschule Flensburg: Construction of a deterministic finite automaton. Retrieved September 9, 2018 .