Power set construction

The power set construction ( Myhill construction or also subset construction ) is a method that converts a nondeterministic finite automaton (NEA) into an equivalent deterministic finite automaton (DEA). The procedure serves as constructive proof for the equivalence of the two machine models.

Basic idea

The states of the constructed deterministic automaton DEA are sets of states of the nondeterministic automaton NEA. A state of the DEA encodes all those states in which the equivalent nondeterministic automaton NEA could be at a certain point in time. A state transition in the DEA is deterministic, since its subsequent state consists of the set of all possible subsequent states that an NEA can reach with a certain input.

The method is called power set construction because the states of the constructed automaton are sets of states of the output automaton and therefore the constructed set of states is part of the power set of the state set of the output automaton.

The power set construction does not necessarily result in a minimal deterministic finite automaton.

Theoretical framework

The scientists Michael O. Rabin and Dana Scott received the Turing Award in 1976 for their work in the field of automata theory . About the sentence named after them

Any language accepted by an NEA is also acceptable by a DEA.

To be able to prove, an algorithm is constructed which assigns an equivalent DEA to each NEA.

construction

For a nondeterministic automaton construct an equivalent deterministic automaton as follows: ${\displaystyle {\mathcal {NA}}=(Q,\Sigma ,\delta ,q_{0},F)}$ ${\displaystyle {\mathcal {A}}=(Q',\Sigma ,\delta ',q_{0}',F')}$

1. Start with empty state sets and . ${\displaystyle Q\!\,'}$ ${\displaystyle F\!\,'}$
2. Choose the starting state of as a one-element set of the starting state of . Add the states to the set . ${\displaystyle q_{0}\!\,'}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle q_{0}\!\,'=\{q_{0}\}}$ ${\displaystyle q_{0}\in Q}$ ${\displaystyle {\mathcal {NA}}}$ ${\displaystyle q_{0}\!\,'}$ ${\displaystyle Q\!\,'}$
3. For all states that are already contained in: ${\displaystyle q\!\,'}$ ${\displaystyle Q\!\,'}$
   • For each input character : ${\displaystyle s\in \Sigma }$
     • Construct a subsequent state as a set of all states that, starting from a state , can be reached by entering . So . ${\displaystyle q''\!\,}$ ${\displaystyle {\mathcal {NA}}}$ ${\displaystyle q'\!\,}$ ${\displaystyle s\!\,}$ ${\displaystyle q'':=\bigcup \{\delta (r,s)|r\in q'\}\!\,}$
     • Add the state to if it is not already included in the set of states of . ${\displaystyle q\!\,''}$ ${\displaystyle Q\!\,'}$ ${\displaystyle {\mathcal {A}}}$
     • Add the transition to the transition function . ${\displaystyle \delta \!\,'}$ ${\displaystyle \delta \!\,'(q',s)=q''}$
4. Repeat step 3. until and no longer change. ${\displaystyle Q\!\,'}$ ${\displaystyle \delta \!\,'}$
5. Choose the set of final states of as the subset of whose states contain a final state from . ${\displaystyle F\!\,'}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle Q\!\,'}$ ${\displaystyle F\!\,}$

Note: can have up to states at the end . However, this is inevitable because there are languages ​​(e.g. ) that are accepted by an NEA with states, but which have Myhill-Nerode equivalence classes , which means that an equivalent DEA must have at least states. ${\displaystyle {\mathcal {A}}}$ ${\displaystyle 2^{|Q|}}$ ${\displaystyle (0|1)^{*}0(0|1)^{n}}$ ${\displaystyle n+2}$ ${\displaystyle 2^{n+1}}$ ${\displaystyle 2^{n+1}}$

Formally

Let be a nondeterministic finite automaton with the set of states , the input alphabet , the transition function , the start state and the set of final states . Continue to be ${\displaystyle A=\left(Q,\Sigma ,\delta ,s,F\right)}$ ${\displaystyle Q\!\,}$ ${\displaystyle \Sigma \!\,}$ ${\displaystyle \delta \colon Q\times (\Sigma \,\cup \{\epsilon \})\to {\mathcal {P}}(Q)\!\,}$ ${\displaystyle s\!\,}$ ${\displaystyle F\!\,}$

${\displaystyle E:Q\rightarrow {\mathcal {P}}(Q)}$so that and , the completion of a state under ${\displaystyle \forall q\in Q:q\in E(q)}$ ${\displaystyle r\in E(q)\Leftrightarrow \exists p\in E(q):r\in \delta (p,\epsilon )}$ ${\displaystyle \epsilon \!\,}$ ${\displaystyle \delta \!\,,}$

${\displaystyle s'\!\,:=E(s)}$, the degree from under ${\displaystyle \!\,\epsilon }$ ${\displaystyle s\!\,}$ ${\displaystyle \delta \!\,,}$

${\displaystyle {\tilde {\delta }}:{\mathcal {P}}(Q)\times \Sigma \to {\mathcal {P}}(Q)}$, With ${\displaystyle {\tilde {\delta }}(q',a):=\bigcup \{E(r)|p\in q',r\in \delta (p,a)\},}$

${\displaystyle Q'\subseteq {\mathcal {P}}(Q)}$so that the smallest amount is with and ${\displaystyle Q'}$ ${\displaystyle s'\in Q'}$ ${\displaystyle \forall q'\in Q',\forall a\in \Sigma :{\tilde {\delta }}(q',a)\in Q',}$

${\displaystyle \delta '\colon Q'\times \Sigma \to Q',\delta ':={\tilde {\delta }}\mid _{Q'\times \Sigma },}$

${\displaystyle F':={\Big \{}q'\in Q'|q'\cap F\neq \emptyset {\Big \}}.}$

From this the deterministic finite automaton , which is too equivalent, results as: ${\displaystyle A\!\,}$ ${\displaystyle A'\!\,}$

${\displaystyle A'=\left(Q',\Sigma ,\delta ',s',F'\right)}$

Examples

Automaton for the regular expression ( a | b ) * aba

Let the nondeterministic automaton be given over the alphabet with the transfer function given in the table : ${\displaystyle {\mathcal {NA}}={\Big (}\{s_{0},s_{1},s_{2},s_{3}\},\Sigma ,\delta ,s_{0},\{s_{3}\}{\Big )}}$ ${\displaystyle \Sigma \!\,=\{a,b\}}$ ${\displaystyle \delta \!\,}$

δ	a	b
${\displaystyle s_{0}\!\,}$	${\displaystyle \{s_{0}\!\,,s_{1}\}}$	${\displaystyle \{s_{0}\}\!\,}$
${\displaystyle s_{1}\!\,}$	${\displaystyle \emptyset }$	${\displaystyle \{s_{2}\}\!\,}$
${\displaystyle s_{2}\!\,}$	${\displaystyle \{s_{3}\}\!\,}$	${\displaystyle \emptyset }$
${\displaystyle s_{3}\!\,}$	${\displaystyle \emptyset }$	${\displaystyle \emptyset }$

A graphic representation of the output machine looks like this:

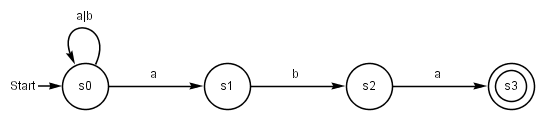
According to the above construction, the quantity of states and the transfer function of the equivalent deterministic automaton result as follows: ${\displaystyle Q\!\,'=\{S_{0}',S_{1}',S_{2}',S_{3}'\}}$ ${\displaystyle \delta \!\,'}$

δ '	a	b
${\displaystyle S_{0}\!\,'=\{s_{0}\}}$	${\displaystyle \{s_{0},s_{1}\}\!\,}$	${\displaystyle \{s_{0}\}\!\,}$
${\displaystyle S_{1}\!\,'=\{s_{0},s_{1}\}}$	${\displaystyle \{s_{0},s_{1}\}\!\,}$	${\displaystyle \{s_{0},s_{2}\}\!\,}$
${\displaystyle S_{2}\!\,'=\{s_{0},s_{2}\}}$	${\displaystyle \{s_{0},s_{1},s_{3}\}\!\,}$	${\displaystyle \{s_{0}\}\!\,}$
${\displaystyle S_{3}\!\,'=\{s_{0},s_{1},s_{3}\}}$	${\displaystyle \{s_{0},s_{1}\}\!\,}$	${\displaystyle \{s_{0},s_{2}\}\!\,}$

The set of final states is derived from this, since only contains the final state of the output automaton . Overall, the deterministic automaton results, which has the following graphic representation: ${\displaystyle F\!\,'=\{S_{3}'\}}$ ${\displaystyle S_{3}\!\,'=\{s_{0},s_{1},s_{3}\}}$ ${\displaystyle s_{3}\!\,}$ ${\displaystyle {\mathcal {A}}=(Q',\Sigma ,\delta ',s_{0}',F')}$

Automaton for the regular expression a ( a | b ) * b

NEA for the regular expression ${\displaystyle a(a|b)^{*}b\!\,}$

δ '	a	b
${\displaystyle S_{0}'=\{s_{0}\}\!\,}$	${\displaystyle \{s_{1}\}\!\,}$	${\displaystyle \emptyset }$
${\displaystyle S_{1}'=\{s_{1}\}\!\,}$	${\displaystyle \{s_{1}\}\!\,}$	${\displaystyle \{s_{1},s_{2}\}\!\,}$
${\displaystyle S_{2}'=\{s_{1},s_{2}\}\!\,}$	${\displaystyle \{s_{1}\}\!\,}$	${\displaystyle \{s_{1},s_{2}\}\!\,}$
${\displaystyle 0=\emptyset }$	${\displaystyle \emptyset }$	${\displaystyle \emptyset }$

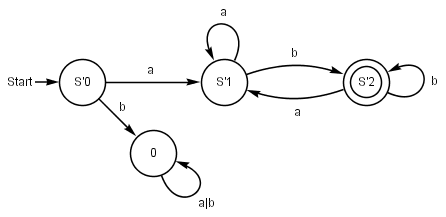
DEA for the regular expression ${\displaystyle a(a|b)^{*}b\!\,}$

See also

• Power automaton