Number of edges

As a number of edges is known in the graph theory , the number of edges of a graph .

If this is the graph under consideration, this number is usually noted with (or briefly , if it is clear which graph it is). Alternatively, you can also write . ${\displaystyle G}$ ${\displaystyle m(G)}$ ${\displaystyle m}$ ${\displaystyle ||G||}$

definition

In the case of undirected graphs, the number of edges of a given graph is the number of its edges, or the sum of the multiples of the individual edges, if it is a graph with multiple edges. ${\displaystyle m(G)}$ ${\displaystyle G=(V,E)}$

It can also be seen as the thickness of the set of edges . ${\displaystyle |E|}$ ${\displaystyle E}$

properties

• The following applies: . Here, the clique number of ; the number of nodes in the largest clique of . Equality occurs with complete graphs . ${\displaystyle m(G)\geq \Delta _{\tau (G)-1}={\frac {\tau (G)(\tau (G)-1)}{2}}}$ ${\displaystyle \tau (G)}$ ${\displaystyle G}$ ${\displaystyle G}$
• Also applies

${\displaystyle m(G)\geq \sum _{v\in U}d(v)}$. is a stable set of and the degree of the knot . If equality occurs, there is a maximally stable set of the graph .
${\displaystyle U}$ ${\displaystyle G}$ ${\displaystyle d(v)}$ ${\displaystyle v}$ ${\displaystyle U}$ ${\displaystyle G}$

Calculation for different classes of graphs

In the following section, simple graphs are always assumed, i.e. undirected graphs without multiple edges .

Complete graph

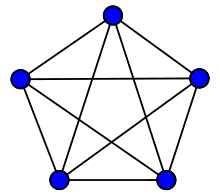
The complete graph with 10 edges ${\displaystyle K_{5}}$

The number of edges of the complete graph with nodes corresponds to ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle K_{n}}$

${\displaystyle m={n \choose 2}={\frac {n(n-1)}{2}}=\Delta _{n-1}}$,

so the triangle number . ${\displaystyle \Delta _{n-1}}$

This can be seen from the fact that each edge is defined by two nodes and there are options to select two nodes. ${\displaystyle {n \choose 2}}$

Trees

Trees with nodes have edges according to Cayley's formula . It is a special case of Euler's polyhedron substitute for planar graphs (see planar graphs). The graph class of trees also includes linear graphs and star graphs . A star graph is a graph that has a central node that is connected to all other nodes. The other nodes only have this one neighbor. ${\displaystyle n}$ ${\displaystyle m=n-1}$

Planar graphs

The number of edges of a planar graph can be calculated using Euler's polyhedron theorem for planar graphs

${\displaystyle n-m+l=2}$.

The area number applies and is . ${\displaystyle n=|V|,m=|E|}$ ${\displaystyle l}$

If you solve the equation for , you get ${\displaystyle m}$

${\displaystyle m=n+l-2}$.

Maximum planar graphs

The Goldner – Harary graph is a maximally planar graph. It has 11 nodes and 27 edges

A maximally planar graph is a graph to which no further edges can be added. If it has at least 3 nodes, it is a triangle graph and each of its areas is surrounded by 3 edges.

The number of edges of a maximal planar graph with at least 3 nodes is . ${\displaystyle m=3n-6}$

Regular graphs

For a regular graph with degrees and nodes, the number of edges is ${\displaystyle k}$ ${\displaystyle n}$

${\displaystyle m={\frac {n\cdot k}{2}}}$.

This is due to the fact that edges emanate from every node ; However, you count each edge twice and therefore have to divide by 2. ${\displaystyle k}$

Given average degree

Given the average degree and number of nodes , the number of edges can be calculated as follows ${\displaystyle d(G)}$ ${\displaystyle n}$

${\displaystyle m={\frac {d(G)\cdot n(G)}{2}}}$.

By multiplying with the number of all edges is in the numerator; however, each is counted twice, so it is divided by 2. ${\displaystyle n}$

This formula is a generalization of the formula for regular graphs.

Bipartite graph

If a given graph is a bipartite graph whose node set can be divided into two disjoint subsets and , then only one maximum can be given for the number of edges. ${\displaystyle G}$ ${\displaystyle V}$ ${\displaystyle V_{1}}$ ${\displaystyle V_{2}}$

Each node can be connected to a maximum of different nodes by an edge. ${\displaystyle v\in V_{1}}$ ${\displaystyle |V_{2}|}$ ${\displaystyle w\in V_{2}}$

So there are at most edges. ${\displaystyle m=|V_{1}|\cdot |V_{2}|}$

Is a complete bipartite graph , then the number of edges is maximum and achieved exactly . ${\displaystyle G}$ ${\displaystyle |V_{1}|\cdot |V_{2}|}$

In general, the maximum number of edges of a k-partite graph with the disjoint subsets is ${\displaystyle G=(V,E)}$ ${\displaystyle k}$ ${\displaystyle V_{1},\dotsc ,V_{k}}$

${\displaystyle {\begin{aligned}m&=\Delta _{|V|-1}-\Delta _{|V_{1}|-1}-\dotsb -\Delta _{|V_{k}|-1}\\&=\left({\frac {|V|(|V|-1)}{2}}\right)-\left({\frac {|V_{1}|(|V_{1}|-1)}{2}}\right)-\left({\frac {|V_{2}|(|V_{2}|-1)}{2}}\right)-\dotsb -\left({\frac {|V_{k}|(|V_{k}|-1)}{2}}\right)\\&={\frac {(|V|^{2}-|V|)-(|V_{1}|^{2}-|V_{1}|)-(|V_{2}|^{2}-|V_{2}|)-\dotsb -(|V_{k}|^{2}-|V_{k}|)}{2}}\\&={\frac {|V|^{2}-|V|-|V_{1}|^{2}+|V_{1}|-|V_{2}|^{2}+|V_{2}|-\dotsb -|V_{k}|^{2}+|V_{k}|}{2}}\\&={\frac {|V|^{2}-|V_{1}|^{2}-|V_{2}|^{2}-\dotsb -|V_{k}|^{2}-|V|+|V_{1}|+|V_{2}|+\dotsb +|V_{k}|}{2}}\\&={\frac {|V|^{2}-|V_{1}|^{2}-|V_{2}|^{2}-\dotsb -|V_{k}|^{2}}{2}}\end{aligned}}}$

Here stands for the -th triangular number . The formula can be derived by considering how many edges are still missing from a complete graph . ${\displaystyle \Delta _{k}}$ ${\displaystyle k}$

Since every - node-colorable graph is also -partite, the above formula can also be used for -node-colorable graphs. ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$

Grid graph

A grid graph with nodes can be represented as a rectangle in which all edges have the same length. ${\displaystyle G_{i,j}}$ ${\displaystyle n=i\cdot j}$

The number of edges can be calculated by first counting the outer edges and then adding the inner ones.

There are

${\displaystyle {\begin{aligned}m_{1}&=(2i-2)+(2j-2)\\&=2i+2j-4\end{aligned}}}$

outer edges and

${\displaystyle {\begin{aligned}m_{2}&=[(i-2)(j-1)]+[(i-1)(j-2)]\\&=i\cdot j-i-2j+2+i\cdot j-j-2i+2\\&=2ij-3i-3j+4\end{aligned}}}$

inner edges. Together that results

${\displaystyle {\begin{aligned}m&=m_{1}+m_{2}\\&=(2i+2j-4)+(2ij-3i-3j+4)\\&=2ij-i-j\end{aligned}}}$

Edge.

Ladder graphs

The ladder graphs , , , and ${\displaystyle L_{1}}$ ${\displaystyle L_{2}}$ ${\displaystyle L_{3}}$ ${\displaystyle L_{4}}$ ${\displaystyle L_{5}}$

A ladder graph has the structure of a ladder. It consists of two linear graphs of equal length (the spars), with two corresponding nodes being connected by an edge (the rungs).

The ladder graph with nodes has edges for the stiles and edges for the rungs, so in total ${\displaystyle L_{n}}$ ${\displaystyle 2n}$ ${\displaystyle 2n-2}$ ${\displaystyle n}$

${\displaystyle m=2n-2+n=3n-2}$

Edge.

Wheel graphs

A wheel graph consists of a circle graph to which another node connected to all nodes has been added. The wheel graph has nodes. ${\displaystyle C_{n}}$ ${\displaystyle W_{n}}$ ${\displaystyle n+1}$

The number of edges of is calculated through ${\displaystyle W_{n}}$

${\displaystyle w=2n}$.

Calculation from an adjacency matrix

If the adjacency matrix of a graph is given, it is very easy to determine the number of edges of this graph.

An adjacency matrix has an entry in the -th row and -th column for an edge that connects the nodes and . If the graph is undirected, the 1 is also in the -th row and -th column. ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle j}$ ${\displaystyle i}$

To calculate the number of edges, you just have to add up all the entries and divide by 2. This procedure also works for graphs with multiple edges.

Graphs that emerge from each other through operations

Dual graphs

For a given graph , the dual graph is created by replacing each area of with a vertex of . In addition, edges that separated areas from become edges that connect the new nodes from . ${\displaystyle G=(V,E)}$ ${\displaystyle G'=(V',E')}$ ${\displaystyle G}$ ${\displaystyle G'}$ ${\displaystyle G}$ ${\displaystyle G'}$

The number of edges remains the same with this method, so the following applies

${\displaystyle m(G)=m(G')}$.

Isomorphic graphs

The fact that two graphs are isomorphic to one another means that they are structurally the same and only differ in the names of the nodes and edges.

Therefore, for two isomorphic graphs and ${\displaystyle G}$ ${\displaystyle G'}$

${\displaystyle m(G)=m(G')}$.

Complement graphs

The Petersen graph (left) and its complement graph (right)

The complement graph of a graph is the graph that has the same set of nodes as , but all edges that do not. ${\displaystyle G=(V,E)}$ ${\displaystyle G'=(V',E')}$ ${\displaystyle V'}$ ${\displaystyle G}$ ${\displaystyle G}$

The number of edges of the complement graph of can be calculated depending on the number of edges of . ${\displaystyle G}$ ${\displaystyle G}$

${\displaystyle {\begin{aligned}m(G')&=\Delta _{n(G)-1}-m(G)\\&={\frac {n(G)(n(G)-1)}{2}}-m(G)\end{aligned}}}$

Stands for the number of nodes . The formula is derived because the union of the two sets of nodes forms a complete graph. ${\displaystyle n(G)}$ ${\displaystyle G}$

Edge graphs

The edge graph of a graph arises when every edge of becomes a node of . Then the nodes of are connected by an edge that was adjacent in. ${\displaystyle L(G)=(V',E')}$ ${\displaystyle G=(V,E)}$ ${\displaystyle G}$ ${\displaystyle L(G)}$ ${\displaystyle L(G)}$ ${\displaystyle G}$

The formula for the number of edges of can be derived from the consideration that every node of is replaced by edges that connect the nodes that have arisen instead of the adjacent edges. ${\displaystyle L(G)}$ ${\displaystyle v\in V}$ ${\displaystyle G}$ ${\displaystyle {\tbinom {d(v)}{2}}=\Delta _{d(v)-1}}$

So it is

${\displaystyle m(L(G))=\sum _{v\in V}{\binom {d(v)}{2}}=\sum _{v\in V}\Delta _{d(v)-1}}$.

See also

• Number of nodes
• Edge (graph theory)