k-context
The k-connection of a graph is an important term in graph theory and a generalization of the connection . The k-relationship is clearly a measure of how difficult it is to split a graph into two components by deleting nodes. If the k-connection is large, many nodes must be deleted.
definition
Undirected graph
An undirected graph (which is also a multi-graph may be) is k-fold knot contiguous (or simply k times contiguously or k-connected ) when there is no separator in a maximum -element set of nodes and empty edge set there. Equivalent to this is that the subgraph induced by is connected for all node sets with cardinality .
If a subset of the node set has the property that the subgraph induced by is -connected and is not -connected for every node set , then one calls a k-connected component of . A 2-connected component is also called a block .
The node connection number (often referred to as the connection number or connection for short ) of a graph is the largest , so that it is connected. An equivalent definition is that the node connection number is the smallest thickness of a separator with an empty set of edges. Graphs k-connected are to have associated numbers , the greater than or equal include .
Directed graph
A directed graph (which may also include multiple edges) is k-fold strongly connected if for each node set of the thickness of the of induced partial graph strongly connected is.
The largest , so that -fold is strongly connected, is called the strong connected number and is denoted by.
example
K-fold connection
As an example, consider the house of Santa Claus on the right . It is 2-connected, as there are no separators that consist of only one node. Equivalent to this is that there is no articulation . But if you look at z. For example, nodes 3 and 4 separate the house into node sets 5 and 1 and 2, since every path from 5 to 1 or 2 must go through one of nodes 3 or 4. So the house is single and twofold nodal and its nodal number is .
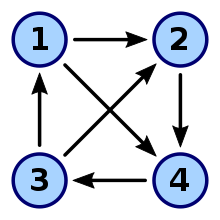
K-fold strong connection
As an example graph, consider the tournament graph shown on the right . The graph is strongly connected, so in any case simply strongly connected. However, if you start deleting single-element sets of nodes, the strong connection is soon destroyed. If you remove z. B. node 3, node 2 can no longer be reached from node 4. Thus the digraph is simply strongly connected and .
properties
- Every -connected graph is also -connected (since there is no -element set of nodes that separates, there are of course no -element sets).
- A simple graph is 2-connected if and only if it has no articulation .
- A 1-connected component is exactly the classic connected component .
- If , then applies where is the edge connection number and the minimum degree of the graph . A high correlation therefore requires a high minimum degree. However, the reverse is not true.
- is -contiguous if and only if there are disjoint paths between two nodes . This statement is also known as the global version of Menger's Theorem .
Algorithms
Determination of the node connection number
There are polynomial algorithms for calculating the node connection number . One can use flow algorithms for this purpose, for example . For this a maximum - - flow is calculated for all pairs of nodes . According to Menger's theorem, the smallest value that the flow assumes is the node connection number. So if the effort required to determine a - -flow in a graph with n nodes and m edges, then this naive approach yields an effort of . However, there are also more efficient algorithms.
A very good but complicated algorithm for calculating the edge connection of a directed (and thus also undirected) graph with rational weights was developed by H. Gabow (based on the matroid theory, i.e. a set of subtrees).
A lighter algorithm that is also suitable for real weights exists, discovered by Stoer / Wagner and at the same time Nagamotchi / Ibaraki. This works by means of node contraction and only for undirected graphs.
A directed graph algorithm based on flow algorithms was presented by Hao / Orlin.
Test for k-connection
If one is not interested in the node connection number, but only wants to know whether a graph is k-connected for a given k, then there are fast algorithms. In this way, the 2-relationship can be determined in linear time. For undirected graphs there are linear algorithms that check a 3-relationship. For 4-connection in undirected graphs there are algorithms with effort
Related terminology
The edge connection is a term similar to the k-connection, except that only separators with an empty set of nodes and an arbitrary set of edges are considered. The edge connection is a measure of how many edges have to be removed from a graph so that it breaks down into different components. A term for directed graphs that is analogous to the edge connection is formed by the arc connection , which considers directed edges instead of undirected edges.
Number of simple non-isomorphic unnamed graphs
Number of different non-isomorphic simple unnamed - connected graphs with nodes for from 1 to 9, including the reference OEIS (simple graphs include both connected and non-connected):
| \ | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | 9 | OEIS |
|---|---|---|---|---|---|---|---|---|---|---|
| easy | 1 | 2 | 4th | 11 | 34 | 156 | 1044 | 12346 | 274668 | A000088 |
| 1 | 1 | 1 | 2 | 6th | 21st | 112 | 853 | 11117 | 261080 | A001349 |
| 2 | 0 | 1 | 1 | 3 | 10 | 56 | 468 | 7123 | 194066 | A002218 |
| 3 | 0 | 0 | 1 | 1 | 3 | 17th | 136 | 2388 | 80890 | A006290 |
| 4th | 0 | 0 | 0 | 1 | 1 | 4th | 25th | 384 | 14480 | A086216 |
| 5 | 0 | 0 | 0 | 0 | 1 | 1 | 4th | 39 | 1051 | A086217 |
| 6th | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 5 | 59 | |
| 7th | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 5 |
Number of different non-isomorphic simple unnamed graphs with nodes and the node connection number :
| \ | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | 9 | OEIS |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 5 | 13 | 44 | 191 | 1229 | 13588 | |
| 1 | 1 | 0 | 1 | 3 | 11 | 56 | 385 | 3994 | 67014 | A052442 |
| 2 | 0 | 1 | 0 | 2 | 7th | 39 | 332 | 4735 | 113176 | A052443 |
| 3 | 0 | 0 | 1 | 0 | 2 | 13 | 111 | 2004 | 66410 | A052444 |
| 4th | 0 | 0 | 0 | 1 | 0 | 3 | 21st | 345 | 13429 | A052445 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 34 | 992 | |
| 6th | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 4th | 54 |
literature
- Reinhard Diestel: graph theory . Springer, Berlin 2010, ISBN 978-3-642-14911-5 (354 pages).
- Lutz Volkmann: Fundamente der Graphentheorie , Springer (Vienna) 1996, ISBN 3-211-82774-9 ( newer, online version "Graphs on all corners and edges" ; PDF; 3.7 MB)
- Alexander Schrijver : Combinatorial optimization . polyhedra and efficiency. Springer, Berlin 2003, ISBN 978-3-540-44389-6 (3 volumes, 1881 pages).











![G [U]](https://wikimedia.org/api/rest_v1/media/math/render/svg/15417781f6a8d7525100038284f7b73c2398645d)

![G [W]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfcfc43e8a330163b0c94df1cdc49eae6cffb5b7)





![G \ left [V \ backslash U \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed1c20ea37f064f4de96b9069daaa68a90807eaf)