Tetrahedral group

A regular tetrahedron, an example of a body with full tetrahedron symmetry

The tetrahedron group is the group of all symmetry elements ( point group ) of the regular and homogeneous tetrahedron (triangular pyramid, quadruple). It is isomorphic to the symmetric group . The regular tetrahedron belongs to the five Platonic solids , the solids with the greatest possible symmetry. It is the simplest of these bodies and the only one that is not point symmetrical . The tetrahedron is dual to itself and therefore has a special position among the five regular solids. ${\displaystyle S_{4}}$

An (arbitrary) tetrahedron has the lowest number of faces, corners and edges of all polyhedra . Because it is simple, it is also called the simplex of three-dimensional space. The (three-dimensional) space cannot be filled with tetrahedra alone (“3D tiling”). In crystals it occurs in the cubic crystal system .

The tetrahedron group is one of the 12 group types with 24 symmetry elements that are not Abelian groups . In molecular physics and crystallography , the full group of the tetrahedron is marked according to the Schoenflies symbology of point groups and space groups with the symbol  and the tetrahedron rotating group with the symbol  . ${\displaystyle T_{d}}$ ${\displaystyle T}$

As with other geometrical bodies , one can distinguish the type of symmetry with symbols of the Schoenflies symbology of the symmetry elements as follows: (rotation), (mirroring), (rotating mirroring) and (inversion or point symmetry, which does not exist in the tetrahedron). The index is used to differentiate counts in rotation and rotation mirroring. ${\displaystyle C_{n}}$ ${\displaystyle \sigma }$ ${\displaystyle S_{n}}$ ${\displaystyle i}$ ${\displaystyle n}$

Division of the spherical surface into fundamental areas according to tetrahedral symmetry

Full tetrahedral group

All 7 axes of rotational symmetry of a regular and homogeneous tetrahedron

Three 2-way axes

Four 3-way axes

Mirror symmetry plane and rotating mirror symmetry axis with rotating mirror plane

One of six mirror symmetry planes

One of three 4-fold rotating mirror symmetry axes with rotating mirror plane

The symmetries of the regular and homogeneous tetrahedron are also explained in the article Tetrahedron . The full tetrahedron group consists of rotations, reflections and rotations , which transform the tetrahedron into itself, and has 24 group elements. The group order is therefore 24. If all four corners (or all four surfaces) of the tetrahedron are numbered, then all 24 possible permutations are actually elements of symmetry of the tetrahedron.

Such a tetrahedron has a total of 7 axes of rotation (axes of rotational symmetry), as shown in the graphic below:

• 3 by the centers of opposite edges and
• 4 which run through opposite corners and surface centers.

The drawn wire frame model of an enveloping cube makes it easier to assign the axes of rotation of a tetrahedron to those of a cube .

In addition, the tetrahedron has the following symmetries:

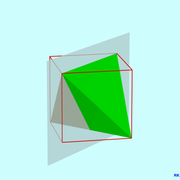
• Six mirror symmetry planes, each running through one edge and perpendicular to the opposite edge. One of them is shown in the first graphic on the right.
• Three 4-fold rotating mirror symmetry axes that run through the centers of opposite edges. Each rotating mirror axis has a rotating mirror plane that goes through the center of symmetry, the midpoint of the tetrahedron, and whose normal vector is the rotating mirror axis of symmetry . One of the three rotating mirror axes of symmetry and the associated rotating mirror plane are shown in the second graphic on the right. As you can see from the graphic, the plane of the rotating mirror is not a plane of mirror symmetry of the tetrahedron. Each rotation mirror adds two symmetries to the tetrahedral group.

The full tetrahedral group is isomorphic to a subgroup of the cube group ( octahedral group ), namely to the cube-rotating group (octahedral rotating group ). This fact is seldom expressed like this: The cube group is a supergroup of the tetrahedral group. ${\displaystyle O_{h}}$ ${\displaystyle O}$

The tetrahedral group is, as already mentioned, isomorphic to the group of permutations of four (any) different objects, to the symmetrical group with the symbol (which is not a Schoenflies symbol). If we use the numbers of the four corners of the first graphic of the tetrahedron and arrange the symmetry elements in the order given above (rotations, reflections, rotations), this results in the following sequence for the 24 permutations : ${\displaystyle S_{4}}$

${\displaystyle T_{d}=\{1234,2143,3412,4321,1423,1342,3241,4213,4132,2431,2314,3124,}$ ${\displaystyle \qquad \quad 1243,1324,1432,2134,4231,3214,4312,3421,4123,2341,3142,2413\}}$.

The 12 rotations in the first line are the even permutations, the 12 reflections and the rotation reflections in the second line are the odd permutations.

With the Schoenflies symbolism of the elements , the elements can be symbolized as follows:

${\displaystyle T_{d}=\{E,C_{2,1},C_{2,2},C_{2,3},C_{3,1},C_{3,1}^{2},C_{3,2},C_{3,2}^{2},C_{3,3},C_{3,3}^{2},C_{3,4},C_{3,4}^{2},}$ ${\displaystyle \qquad \quad \sigma _{d,1},\sigma _{d,2},\sigma _{d,3},\sigma _{d,4},\sigma _{d,5},\sigma _{d,6},S_{4,1},S_{4,1}^{3},S_{4,2},S_{4,2}^{3},S_{4,3},S_{4,3}^{3}\}}$.

The symbol stands for the neutral element. The symbols (rotation), (mirroring) and (rotating mirroring) characterize the symmetry type. The second index consecutively numbers elements of the same type. For example, a threefold rotation and means the first element of this type. A power, for example , means the product (linkage) of the element with itself, the third power of the element . ${\displaystyle E}$ ${\displaystyle C_{n}}$ ${\displaystyle \sigma _{d}}$ ${\displaystyle S_{n}}$ ${\displaystyle C_{3,1}}$ ${\displaystyle C_{3,1}^{2}}$ ${\displaystyle C_{3,1}}$ ${\displaystyle S_{4,1}^{3}}$ ${\displaystyle S_{4,1}}$

We can freely choose the order of the elements. We make use of this and now rearrange the mirror and rotating mirror symmetries in such a way that the order is analogous to the order of the rotational symmetries. To do this, we link each element of the first 12 symmetries with the element of the first mirror symmetry and use the resulting sequence for the connection table. The 13th element is then , the 14th , etc. ${\displaystyle \sigma _{d,1}}$ ${\displaystyle E*\sigma _{d,1}=\sigma _{d,1}}$ ${\displaystyle C_{2,1}*\sigma _{d,1}=\sigma _{d,4}}$

For the interpretation of the link table in color, it is also advantageous to underlay the element symbols in this new order with colors. We highlight the neutral element with the color black, the second highlighted mirror symmetry element with the color white: ${\displaystyle E}$ ${\displaystyle \sigma _{d,1}}$

${\displaystyle T_{d}=\{}$ ${\displaystyle \color {white}E,}$ ${\displaystyle C_{2,1},}$ ${\displaystyle C_{2,2},}$ ${\displaystyle C_{2,3},}$ ${\displaystyle C_{3,1},}$ ${\displaystyle C_{3,1}^{2},}$ ${\displaystyle C_{3,2},}$ ${\displaystyle C_{3,2}^{2},}$ ${\displaystyle C_{3,3},}$ ${\displaystyle C_{3,3}^{2},}$ ${\displaystyle C_{3,4},}$ ${\displaystyle C_{3,4}^{2},}$

             ${\displaystyle \sigma _{d,1},}$ ${\displaystyle \sigma _{d,4},}$ ${\displaystyle S_{4,1}^{3},}$ ${\displaystyle S_{4,1},}$ ${\displaystyle \sigma _{d,3},}$ ${\displaystyle \sigma _{d,2},}$ ${\displaystyle \sigma _{d,6},}$ ${\displaystyle \sigma _{d,5},}$ ${\displaystyle S_{4,2},}$ ${\displaystyle S_{4,3}^{3},}$ ${\displaystyle S_{4,2}^{3},}$ ${\displaystyle S_{4,3}}$ ${\displaystyle \}}$.

Link panel

With a truth table or group table , in the sciences and group multiplication table or group multiplication table , called the bonding product (product) is placed between two group elements in the form of a table. The agreement applies that the symmetry operation arranged in the first line, the header line, is carried out first and then the symmetry operation arranged in the first column, the input column, is carried out. A separate title line and title column, as practiced in most relevant Wikipedia articles, is not absolutely necessary as it is redundant. The product of both elements is at the intersection of row and column. If all products commutate ( Abelian group ), the table (linkage table) is symmetrical with respect to the main diagonal , which is not the case with the tetrahedral group.

In the graphic, the elements of the tetrahedron group are represented by colored squares and, accordingly, the link table is also shown in color, in the new order introduced above. The first 12 symmetry operations are rotations (the twofold operations first). This type of display of link tables in color can also be found in more modern online publications, for example in the online encyclopedia for mathematics MathWorld .

The following conclusions can be drawn from the graphic link table:

• If the product of an element with itself is the neutral element, then the product lies on the main diagonal (provided that the elements are arranged in the same order in the header and the input column). Then the element is inverse to itself, so it has the element order 2. This applies to 9 group elements (and the neutral element).

Linking table of the tetrahedral group T _d and the symmetrical group S ₄ in color. The neutral element is black, the first mirror symmetry element is white

• All elements of order 2 always form a subgroup of order 2 with the neutral element. So also this 9. There cannot be any further subgroups of order 2. One of them are the first two elements. There is only one group type for two elements (it can optionally be symbolized with , or ). ${\displaystyle C_{2}}$ ${\displaystyle D_{1}}$ ${\displaystyle S_{2}}$
• The first four elements form a subgroup, because the colors of your products remain in the first 4x4 block and the colors are symmetrical with respect to the main diagonals. This subgroup is therefore Abelian. It is of the Klein group of four group type (and also the only subgroup of the tetrahedral group of the normal divisor type , which is not to be discussed in more detail here).
• The first 12 elements also form a subgroup that is not Abelian. It is the tetrahedral rotating group .
• The product of a rotational symmetry element (block with the colors red to green) with a mirror or rotating mirror symmetry element (block with the colors light blue to purple) is a mirror or rotating mirror symmetry element and vice versa.
• The product of a mirror or rotating mirror symmetry element with a mirror or rotating mirror symmetry element is a rotationally symmetrical element.
• By rearranging elements 13 to 24, we have achieved that the structure of the first diagonal block is found in the right secondary diagonal block and the structure of the second diagonal block in the left secondary diagonal block.

In principle, these conclusions can be drawn from any type of linkage table, including those with symbols. However, they are only particularly evident in a link table in color, especially if the color black is selected for the neutral element . In order to determine further properties of the group, in particular classes and all subgroups, from the link table, it is advisable to use a computer program even with a group order of 24.

Classes

The elements of any group are differentiated according to conjugation classes , which in the natural sciences are usually called classes for short . Each element belongs to one and only one class. In the case of symmetries of simple geometric bodies, the assignment to classes as a type of symmetry is (more or less) "clear" (except for rotating mirror symmetries ). In the case of higher-order abstract groups, a computer program is required to determine the classes of a group.

The number of classes is equal to the number of irreducible representations of the group using matrices , which are particularly important for applications in physics.

The tetrahedron group consists of 5 classes. The number of classes is called, analogous to group order, the class order of the group, which is 5 here. These are: The trivial class with the neutral element , 3 elements of the symmetry type (rotation), 8 elements of the type (rotation), 6 elements of the type (mirroring) and 6 elements of the type (rotating mirroring). ${\displaystyle E}$ ${\displaystyle C_{2}}$ ${\displaystyle C_{3}}$ ${\displaystyle \sigma _{d}}$ ${\displaystyle S_{4}}$

Subgroups

The full tetrahedral group has (not counting the full group) 29 subgroups:

1 trivial group ${\displaystyle :\;\{E\}}$

3 cyclic groups ${\displaystyle C_{2}:\;\{E,C_{2,1}\},\{E,C_{2,2}\},\{E,C_{2,3}\}}$

6 dihedral groups ${\displaystyle D_{1}:\;\{E,\sigma _{d,1}\},\{E,\sigma _{d,2}\},\{E,\sigma _{d,3}\},\{E,\sigma _{d,4}\},\{E,\sigma _{d,5}\},\{E,\sigma _{d,6}\}}$

4 cyclic groups ${\displaystyle C_{3}:\;\{E,C_{3,1},C_{3,1}^{2}\},\{E,C_{3,2},C_{3,2}^{2}\},\{E,C_{3,3},C_{3,3}^{2}\},\{E,C_{3,4},C_{3,4}^{2}\}}$

1 Klein group of four ${\displaystyle V:\;\{E,C_{2,1},C_{2,2},C_{2,3}\}}$

3 dihedral groups ${\displaystyle D_{2}:\;\{E,C_{2,1},\sigma _{d,1},\sigma _{d,4}\},\{E,C_{2,2},\sigma _{d,3},\sigma _{d,6}\},\{E,C_{2,3},\sigma _{d,2},\sigma _{d,5}\}}$

3 rotating mirror groups ${\displaystyle S_{4}:\;\{E,C_{2,1},S_{4,1},S_{4,1}^{3}\},\{E,C_{2,2},S_{4,2},S_{4,2}^{3}\},\{E,C_{2,3},S_{4,3},S_{4,3}^{3}\}}$

4 dihedral groups ${\displaystyle D_{3}:\;\{E,C_{3,1},C_{3,1}^{2},\sigma _{d,1},\sigma _{d,2},\sigma _{d,3}\},\{E,C_{3,2},C_{3,2}^{2},\sigma _{d,1},\sigma _{d,5},\sigma _{d,6}\},}$ ${\displaystyle \qquad \qquad \qquad \qquad \quad \{E,C_{3,3},C_{3,3}^{2},\sigma _{d,3},\sigma _{d,4},\sigma _{d,5}\},\{E,C_{3,4},C_{3,4}^{2},\sigma _{d,2},\sigma _{d,4},\sigma _{d,6}\}}$

3 dihedral groups ${\displaystyle D_{4}:\;\{E,C_{2,1},C_{2,2},C_{2,3},\sigma _{d,1},\sigma _{d,4},S_{4,1},S_{4,1}^{3}\},\{E,C_{2,1},C_{2,2},C_{2,3},\sigma _{d,2},\sigma _{d,5},S_{4,2},S_{4,2}^{3}\},}$ ${\displaystyle \qquad \qquad \qquad \qquad \quad \{E,C_{2,1},C_{2,2},C_{2,3},\sigma _{d,3},\sigma _{d,6},S_{4,3},S_{4,3}^{3}\}}$

1 tetrahedron rotating group ${\displaystyle T:\;\{E,C_{2,1},C_{2,2},C_{2,3},C_{3,1},C_{3,1}^{2},C_{3,2},C_{3,2}^{2},C_{3,3},C_{3,3}^{2},C_{3,4},C_{3,4}^{2}\}}$

Of these, only the trivial subgroup and Klein's group of four are of the normal divisor type .

Body with full tetrahedral symmetry

Type	Surname	image	Surfaces	Corners	edge
Platonic solid	Tetrahedron		4th	4th	6th
Archimedean body	Truncated tetrahedron		8th	12	18th
Catalan body	Triacistrahedron		12	8th	18th
Almost Johnson body	Triakis tetrahedron		16	28	42
	Tetrated dodecahedron		28	28	54
Regular star body	Tetrahemihexahedron		7th	6th	12

Tetrahedron rotating group

→ Main article : A4 (group)

Representation of the tetrahedron rotating group as a cycle graph

A regular and homogeneous tetrahedron has 7 axes of rotation and is invariant to 11 different rotations around these axes. The group of rotations of the tetrahedron, the tetrahedron rotation group , consequently has 12 elements (including the neutral element). It is the only subgroup of the tetrahedral group of order 12. The linking table for the tetrahedron rotating group is identical to the first 12x12 block (with the colors red to green) of the linking table for the full tetrahedral group above. ${\displaystyle T}$ ${\displaystyle T_{d}}$

The tetrahedron rotation group is not Abelian. It is isomorphic to the alternating group described in article A4 (group) . The elements are symbolized there by consecutive letters, possibly with indices and powers: ${\displaystyle A_{4}}$

${\displaystyle A_{4}=\left\{e,a,b,c,d_{1},d_{1}^{2},d_{2},d_{2}^{2},d_{3},d_{3}^{2},d_{4},d_{4}^{2}\right\}}$.

In the Schoenflies symbolism of the elements, this corresponds to the following elements:

${\displaystyle T=\left\{E,C_{2,1},C_{2,2},C_{2,3},C_{3,1},C_{3,1}^{2},C_{3,2},C_{3,2}^{2},C_{3,3},C_{3,3}^{2},C_{3,4},C_{3,4}^{2}\right\}}$.

The main article also shows a graphic of the tetrahedron and the assignment of the group elements to permutations (the four corners of the tetrahedron) as well as the two principally different types of rotation axes (edge ​​center to edge center or corner to surface center). In addition, two types of linking tables in this group are shown, one in which the elements and their products are symbolized by letters and numbers, and a second by colored squares.

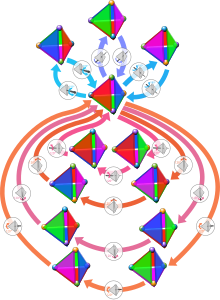
The graphic shows the elements of the tetrahedron rotation group as a cycle graph . The starting and end point of all arrows is the neutral element. The three twofold rotations (around the middle of the edges) are shown as blue arrows and the four threefold rotations as red arrows. The coloring of the surfaces of the tetrahedra only serves to illustrate the symmetry operations, because a tetrahedron whose side surfaces are colored as in the graphic does not have any symmetries.

Classes

The tetrahedron rotation group consists of 4 classes (all of the symmetry type rotation ). These are: The trivial class with the neutral element , 3 elements of the type (in the graphic cycle graph this means the three upper tetrahedra), 4 elements of the type (the four lower right) and 4 elements of the type (the four left lower). ${\displaystyle E}$ ${\displaystyle C_{2}}$ ${\displaystyle C_{3}}$ ${\displaystyle C_{3}^{2}}$

Subgroups

The tetrahedron rotating group has 9 subgroups (again not counting the complete group): The trivial subgroup of order 1, three of order 2, 4 of order 3 and one of order 4. Which elements belong to which subgroup can be found in the main article . In the case of the tetrahedral rotation group, only the trivial subgroup and the subgroup of order 4 are of the normal divisor type .

The tetrahedron rotation group has no subgroup of order 6, although such a subgroup would not contradict Lagrange's theorem (the order of the subgroup is a divisor of the order of the group).

Related group type

In addition, it should be noted that there is a group of the above-mentioned 12 non-Abelian group types of order 24 with the Schoenflies symbol . This has 8 classes. These are: The trivial class with the neutral element, 4 elements of the type , 4 elements of the type , 3 elements of the type , one element of the type (inversion), 4 elements of the type (rotation mirroring), 4 elements of the type and 3 elements of the Type (reflection). ${\displaystyle T_{h}}$ ${\displaystyle C_{3}}$ ${\displaystyle C_{3}^{2}}$ ${\displaystyle C_{2}}$ ${\displaystyle i}$ ${\displaystyle S_{6}}$ ${\displaystyle S_{6}^{5}}$ ${\displaystyle \sigma _{h}}$

See also

• Octahedral group
• Icosahedral group
• polyhedron
• Platonic solid
• Tetrahedron

literature

• Arthur Schoenflies: Crystal systems and crystal structure . Teubner, Leipzig 1891 (XII, 638 p., Online resources ).
• John S. Lomont: Applications of finite groups . Reprint edition. Dover Publications, New York 1993, ISBN 0-486-67376-6 (XI, 346 pp.). Reprint of the edition: Academic Press, New York 1959
• Henry Margenau , George Moseley Murphy: The mathematics for physics and chemistry: Volume I. Chapter XV. Group theory . Teubner, Leipzig 1964 (724 pages).
• Arthur P. Cracknell: Applied Group Theory . Akademie-Verlag [ua], Berlin 1971, ISBN 3-528-06084-0 (453 pages).
• Harold Scott MacDonald Coxeter : Regular polytopes . 3rd ed., Unabridged and corr. repr. of the 2nd ed., New York, Macmillan, 1963. Dover Publications, New York 1973, ISBN 0-486-61480-8 (XIII, 321 pp., limited preview in Google Book Search [accessed January 25, 2020 ]). The preview does not contain any page numbering.
• Frank Albert Cotton : Chemical applications of group theory . 3rd ed. Wiley, New York, NY 1990, ISBN 0-471-51094-7 (XIV, 461 pages).

Web links

• Tetrahedral Group, Mathworld
• Tetrahedral group and symmetrical group S ₄
• Symmetric group S ₄

Individual evidence

1. ↑ Schoenflies 1891, p. 74 and p. 102, group types are named by Schoenflies crystal classes . He calls the trivial group, which consists only of the neutral element, identity and also symbolizes it . ${\displaystyle C_{1}}$
2. ↑ If, for example, the six faces of a dice are numbered like on a game dice , then by no means all 720 possible permutations are symmetry elements of the dice.
3. ↑ It is a symbol of abstract group theory, that branch of group theory that deals with symmetries without direct reference to geometric bodies.
4. ↑ In the case of inversely symmetrical bodies, for example in the case of the cube, the rotational symmetries will be linked with the inversion.
5. ↑ BL van der Waerden: Modern Algebra . 3rd improved edition. Springer-Verlag, Berlin, Göttingen, Heidelberg 1950, p. 24 (VIII, 292).
6. ↑ Cracknell 1971, p. 16
7. ↑ Margenau 1964, p. 664
8. ↑ MathWorld: Tetrahedral Group Note the following differences: In the color graphic of the link table shown above, the neutral element is highlighted as a black square, which is not the case in the color graphic in MathWorld. In addition, the order of the elements is different. The MathWorld site does not state which order was chosen for the color graphics.
9. ↑ Cracknell 1971, p. 24 ff.
10. ↑ Margenau 1964, p. 665 f.
11. ↑ Cracknell 1971, p. 36 ff.
12. ↑ Note that the symbol here means a symbol of the Schoenflies symbolism. The symbol as a symbol of a special symmetrical group does not belong to the Schoenflies symbolism. What is meant by the symbol should be understandable from the context. ${\displaystyle S_{4}}$ ${\displaystyle S_{4}}$
13. ↑ Cotton 1990, p. 47 and p. 434
14. ↑ Convex polyhedra, the faces of which are almost regular polygons , some or all of which are not exactly regular. Related to the Johnson bodies , see near-miss Johnson solid .
15. ↑ English Name Truncated triakis tetrahedron .
16. ↑ German name unknown. That is why the English name Tetrated dodecahedron is listed in the table .
17. ↑ A non-convex regular body. Therefore Euler's polyhedron substitute does not apply.
18. ↑ English name Tetrahemihexahedron .
19. ↑ Cotton 1990, p. 50 and p. 433
20. ↑ Schoenflies 1891, p. 102
21. ↑ Cotton 1990, p. 50 and p. 434