Rotating mirror group

Antiprism with the symmetry group ${\displaystyle S_{4}}$

The rotating mirror group is the symmetry group created by the rotating mirroring to the angle of rotation . If the basic operation is rotation inversion instead of rotation mirroring, that is, the concatenation of the rotation with an inversion at a point on the axis of rotation, the group is created ; the term "rotation inversion group", which is obvious in itself, is not in use. The groups of these two types are the same except for the numbering. Rotating mirror groups appear when describing the symmetry of crystals or individual molecules. In crystallography , only the five groups  = 1, 2, 3, 4 and 6 are relevant, since only these are compatible with the symmetry of an infinitely extended lattice. They belong to the 32 crystallographic point groups . Other groups are also important in studying molecular symmetry . There is an excited form of the anion [Re ₂ Cl ₈ ] ²⁻ with symmetry. ${\displaystyle S_{n}}$ ${\displaystyle \varphi =2\pi /n=360^{\circ }\!/n}$ ${\displaystyle {\overline {n}}}$ ${\displaystyle n}$ ${\displaystyle S_{8}}$

The symmetry group dealt with here must not be confused with the symmetric group . ${\displaystyle S_{n}}$ ${\displaystyle S_{n}}$

notation

There are two designation systems for the rotating mirror groups : The Hermann Mauguin symbolism , mainly used in crystallography , which is based on the rotational inversion as a basic operation for numbering, and the Schoenflies symbolism , which is common in chemistry and molecular physics . ${\displaystyle S_{n}}$

	${\displaystyle S_{1}}$	${\displaystyle S_{2}}$	${\displaystyle S_{n}}$( ) ${\displaystyle n=4k}$	${\displaystyle S_{n}}$( ) ${\displaystyle n=4k+2}$	${\displaystyle S_{n}}$( odd) ${\displaystyle n}$
Hermann Mauguin	${\displaystyle {\text{m}}\;(={\overline {2}})}$	${\displaystyle {\overline {1}}}$	${\displaystyle {\overline {n}}}$	${\displaystyle {\overline {n/2}}}$	${\displaystyle {\overline {2n}}\;(=n/{\text{m}})}$
Schoenflies	${\displaystyle C_{\textrm {s}}}$	${\displaystyle C_{\textrm {i}}}$	${\displaystyle S_{n}}$	${\displaystyle S_{n}\;(=C_{{\frac {n}{2}}{\textrm {i}}})}$	${\displaystyle C_{n{\textrm {h}}}}$

“M” stands for “mirror plane”, “s” for “mirror plane”, “i” for “inversion”, “h” for “horizontal mirror plane” (with a vertical axis of rotation) and “ ” for n-fold rotational symmetry ("C" for "cyclic"); see the section "Properties" . ${\displaystyle C_{n}}$

Examples

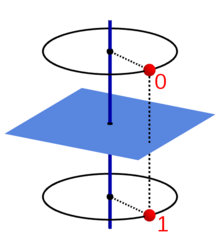
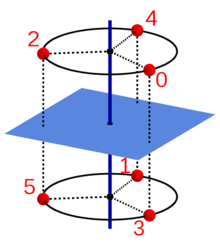
A point in position 0 is successively transferred to positions 1, 2, ... and finally back to starting position 0 by repeated application of the basic operation (rotational mirroring or rotational inversion). The figures below show this application of the group elements to point 0 for some values ​​of . ${\displaystyle g}$ ${\displaystyle g^{k}}$ ${\displaystyle n}$

	${\displaystyle n=1}$	${\displaystyle n=2}$	${\displaystyle n=3}$	${\displaystyle n=4}$	${\displaystyle n=6}$
${\displaystyle S_{n}}$
${\displaystyle {\overline {n}}}$

A body with a - or - symmetry that contains the point 0 must also contain the points 1, 2, ... which are symmetrical to this. One example is the antiprism shown above, in which the four-fold rotating mirror axis is perpendicular to the two top surfaces, with these being oriented differently here . With the same orientation, the body would no longer be a rotating mirror - but instead still rotationally symmetrical, namely around three 2-fold axes (perpendicular to the top surfaces and parallel to their bisector). In the case of non-oriented cover surfaces, both symmetries would occur at the same time. ${\displaystyle S_{n}}$ ${\displaystyle {\overline {n}}}$

properties

The rotating mirror group is cyclic with the order (for odd ) or (for even ). It is therefore particularly commutative . ${\displaystyle S_{n}}$ ${\displaystyle 2n}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle S_{n}}$contains the reflection if and only if is odd, and the inversion if and only if is even but not divisible by 4. ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle S_{n}}$has only rotating groups and rotating mirror groups as subgroups , namely is

• the rotation group subgroup if and only if is a divisor of (for odd ) or of (for even ); ${\displaystyle C_{n'}}$ ${\displaystyle n'}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n/2}$ ${\displaystyle n}$
• the rotating mirror group subgroup if and only if is odd. ${\displaystyle S_{n'}}$ ${\displaystyle n/{n'}}$

The relationship exists between the and the rotating mirror groups ${\displaystyle {\overline {n}}}$

${\displaystyle {\overline {n}}={\begin{cases}S_{n},&{\text{wenn }}n{\text{ durch 4 teilbar ist,}}\\S_{n/2},&{\text{wenn }}n{\text{ gerade, aber nicht durch 4 teilbar ist,}}\\S_{2n},&{\text{wenn }}n{\text{ ungerade ist .}}\end{cases}}}$

Web links

Commons : Rotoreflection groups  - collection of images, videos and audio files

Individual evidence

1. ↑ There are only two search hits for "rotation inversion group" on Google Books . In one of the two (Konrad Altmann: Fundamentals of the theory of infrared, Raman and hyper-Raman spectra of molecular gases, shown using irreducible spherical tensors . University of Munich, 1976) it says: “Actually better rotation inversion group. However, this term is not used in German-language literature. "
2. ^ Bill Trogler: Molecular Symmetry. (PDF; 3.8 MB) (Chapter of the lecture notes for the lecture UCSD Chem 224: Group Theory and Spectroscopy ). University of California, San Diego, 2012, pp. 11-12 , accessed May 2, 2018 . 
3. ^ Walter Borchardt-Ott: Crystallography . 2nd Edition. Springer, 1995, ISBN 3-540-59478-7 .
4. ↑ ^{a b} Daniel Arovas: Crystal Math. (PDF; 9.6 MB) (Chapter 5 of the lecture notes for the lecture UCSD Physics 220: Group Theory ). University of California, San Diego, 2016, accessed May 1, 2018 . 
5. ↑ ^{a b c} Arthur Schoenflies : Crystal systems and crystal structure . Teubner, 1891, p. 81 ( scan [PDF; 16.7 MB ]).