Sign (permutation)

The sign , also known as the sign , signature or parity , is an important number of permutations in combinatorics . The sign of a permutation can take the values or , in the first case one speaks of an even and in the second case of an odd permutation. ${\displaystyle +1}$ ${\displaystyle -1}$

There are several ways to characterize even and odd permutations. A permutation is even if the number of errors in the permutation is even . Each permutation can also be represented as a concatenation of a finite number of transpositions and is even if the number of transpositions required is even. A permutation can also be broken down into cycles and is even if the number of cycles of even length is even. The sign of a permutation is also equal to the determinant of the associated permutation matrix .

As a mapping, the sign is a group homomorphism from the symmetrical group of permutations into the multiplicative group above the set . An important application example of the sign is the Leibniz formula for determinants . ${\displaystyle \{+1,-1\}}$

definition

If the set is the symmetric group of all permutations , then the sign of a permutation is given by ${\displaystyle S_{n}}$ ${\displaystyle \{1,\ldots ,n\}}$ ${\displaystyle \pi =(\pi (1),\pi (2),\ldots ,\pi (n))\in S_{n}}$

${\displaystyle \operatorname {sgn}(\pi )=(-1)^{|\operatorname {inv} (\pi )|}}$

defined, where

${\displaystyle \operatorname {inv} (\pi )=\{~(i,j)\in \{1,\ldots ,n\}\times \{1,\ldots ,n\}\mid i<j,\pi (i)>\pi (j)~\}}$

is the set of permutation errors .

${\displaystyle |\operatorname {inv} (\pi )|}$stands for the thickness (number of elements) of . ${\displaystyle \operatorname {inv} }$

If the sign is called the permutation even, if it is , it is called odd. ${\displaystyle +1}$ ${\displaystyle \pi }$ ${\displaystyle -1}$

In a more general way, permutations of any finite ordered sets can be considered, but the mathematical analysis can be limited to the first natural numbers. ${\displaystyle n}$

Examples

Permutations in S ₃

permutation	Deficiencies	Signum
${\displaystyle {\tbinom {\,1~2~3\,}{\,1~2~3\,}}}$	-	+1
${\displaystyle {\tbinom {\,1~2~3\,}{\,1~3~2\,}}}$	(2.3)	−1
${\displaystyle {\tbinom {\,1~2~3\,}{\,2~1~3\,}}}$	(1.2)	−1
${\displaystyle {\tbinom {\,1~2~3\,}{\,2~3~1\,}}}$	(1.3), (2.3)	+1
${\displaystyle {\tbinom {\,1~2~3\,}{\,3~1~2\,}}}$	(1.2), (1.3)	+1
${\displaystyle {\tbinom {\,1~2~3\,}{\,3~2~1\,}}}$	(1.3)	−1

The imperfections of the permutation

${\displaystyle \pi ={\begin{pmatrix}1&2&3&4&5\\2&1&4&5&3\end{pmatrix}}\in S_{5}}$

are and , thus is ${\displaystyle (1,2),(3,5)}$ ${\displaystyle (4,5)}$

${\displaystyle \operatorname {sgn}(\pi )=(-1)^{3}=-1}$

and thus the permutation is odd. The identical permutation

${\displaystyle \operatorname {id} ={\begin{pmatrix}1&2&\cdots &n\\1&2&\cdots &n\end{pmatrix}}\in S_{n}}$

is always straight because it has no defects. The table opposite lists all permutations of length three with their associated signs.

Presentation as a product

Product formula

The sign of a permutation of the first natural numbers can also be given by the product formula ${\displaystyle n}$

${\displaystyle \operatorname {sgn}(\pi )=\prod _{1\leq i<j\leq n}{\frac {\pi (j)-\pi (i)}{j-i}}}$

being represented. Due to the bijectivity a permutation this case each term occurs for the exception of possibly sign denominator once each in the numerator and once a fracture on. Each deficit leads to exactly one negative sign. ${\displaystyle j-i}$ ${\displaystyle 1\leq i<j\leq n}$

example

The sign of the permutation

${\displaystyle \pi ={\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}\in S_{3}}$

is through

${\displaystyle {\begin{aligned}\operatorname {sgn}(\pi )&={\frac {\pi (2)-\pi (1)}{2-1}}\cdot {\frac {\pi (3)-\pi (1)}{3-1}}\cdot {\frac {\pi (3)-\pi (2)}{3-2}}\\&={\frac {1-3}{2-1}}\cdot {\frac {2-3}{3-1}}\cdot {\frac {2-1}{3-2}}\\&={\frac {2-1}{2-1}}\cdot {\frac {1-3}{3-1}}\cdot {\frac {2-3}{3-2}}\\&=(+1)\cdot (-1)\cdot (-1)=+1\end{aligned}}}$

given. The two faulty items and lead it to each one sign change. ${\displaystyle (1,2)}$ ${\displaystyle (1,3)}$

Concatenation property

The following applies to the sign of a concatenation of two permutations due to the product representation: ${\displaystyle \tau ,\pi \in S_{n}}$

${\displaystyle {\begin{aligned}\operatorname {sgn}(\tau \circ \pi )&=\prod _{i<j}{\frac {\tau (\pi (j))-\tau (\pi (i))}{j-i}}=\prod _{i<j}{\frac {\tau (\pi (j))-\tau (\pi (i))}{\pi (j)-\pi (i)}}\cdot \prod _{i<j}{\frac {\pi (j)-\pi (i)}{j-i}}=\\&=\prod _{\pi ^{-1}(i)<\pi ^{-1}(j)}{\frac {\tau (j)-\tau (i)}{j-i}}\cdot \prod _{i<j}{\frac {\pi (j)-\pi (i)}{j-i}}=\operatorname {sgn}(\tau )\cdot \operatorname {sgn}(\pi )\end{aligned}}}$

The last step follows from the fact that the same factors appear in the product as in the product above , only in a different order. For two numbers that have been swapped , the sign is reversed in both the denominator and the numerator. Accordingly, the concatenation of two permutations is even if and only if both permutations have the same sign. ${\displaystyle \pi ^{-1}(i)<\pi ^{-1}(j)}$ ${\displaystyle i<j}$ ${\displaystyle \pi }$ ${\displaystyle i,j}$

Further representations

Representation of the number of transpositions

Conversion between even and odd permutations through transpositions

A transposition with is a permutation that only swaps the two numbers and , that is, maps onto and onto and leaves the other numbers fixed. The following applies to the sign of a transposition ${\displaystyle \tau _{kl}}$ ${\displaystyle k<l}$ ${\displaystyle k}$ ${\displaystyle l}$ ${\displaystyle k}$ ${\displaystyle l}$ ${\displaystyle l}$ ${\displaystyle k}$

${\displaystyle \operatorname {sgn}(\tau _{kl})=-1}$,

because every transposition can be an odd number of Nachbarvertauschungen the mold as the concatenation by ${\displaystyle \tau _{k,k+1}}$

${\displaystyle \tau _{kl}=(\tau _{l-1,l}\circ \tau _{l-2,l-1}\circ \cdots \circ \tau _{k+1,k+2})\circ (\tau _{k,k+1}\circ \cdots \circ \tau _{l-2,l-1}\circ \tau _{l-1,l})}$

represent. Here, the number is first by successive Nachbarvertauschungen the place taken and then the number of the place by successive Nachbarvertauschungen the place . Since each of these neighboring swaps produces exactly one missing position, the total number of missing positions is a transposition ${\displaystyle l}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k+1}$ ${\displaystyle l}$

${\displaystyle |\operatorname {inv} (\tau _{kl})|=(l-k)+(l-k-1)=2(l-k)-1}$

and therefore always odd. Each permutation can now be represented as a chain of at most transpositions. Each of these transpositions swaps the smallest number for which applies with the number for which applies. If the number of transpositions required is then the following applies due to the chaining property ${\displaystyle \pi \in S_{n}}$ ${\displaystyle n-1}$ ${\displaystyle k}$ ${\displaystyle \pi (k)\neq k}$ ${\displaystyle l>k}$ ${\displaystyle \pi (l)=k}$ ${\displaystyle M(\pi )}$

${\displaystyle \operatorname {sgn}(\pi )=(-1)^{M(\pi )}}$.

There are of course other ways of representing a permutation as a chain of transpositions. However, if the permutation is even, then the number of transpositions required is always even; if the permutation is odd, it is always odd.

example

The permutation

${\displaystyle \pi ={\begin{pmatrix}1&2&3&4\\3&2&4&1\end{pmatrix}}\in S_{4}}$

lets through

${\displaystyle \pi =\tau _{34}\circ \tau _{14}={\begin{pmatrix}1&2&3&4\\1&2&4&3\end{pmatrix}}\circ {\begin{pmatrix}1&2&3&4\\4&2&3&1\end{pmatrix}}}$

represent and is thus straight. Another representation of as a chain of transpositions would be . ${\displaystyle \pi }$ ${\displaystyle \pi =\tau _{23}\circ \tau _{12}\circ \tau _{23}\circ \tau _{34}}$

Representation of the number and length of the cycles

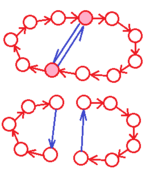
By executing a permutation (red) with an exchange (blue) one after the other, the number of cycles increases by one if the exchanged elements are within a cycle (left) and it is reduced by one if they are in different cycles (right) .

A cyclic permutation is a permutation that the numbers cyclically changed over , that is, on maps, on to on and to be the other numbers. A cyclic permutation of length two corresponds to a transposition of two numbers. Every cyclic permutation of length can be written as a chain of transpositions: ${\displaystyle \sigma _{k_{1},\ldots ,k_{m}}}$ ${\displaystyle k_{1},\ldots ,k_{m}}$ ${\displaystyle k_{1}}$ ${\displaystyle k_{2}}$ ${\displaystyle k_{2}}$ ${\displaystyle k_{3}}$ ${\displaystyle k_{m}}$ ${\displaystyle k_{1}}$ ${\displaystyle m>1}$ ${\displaystyle m-1}$

${\displaystyle \sigma _{k_{1},\ldots ,k_{m}}=\tau _{k_{1},k_{2}}\circ \cdots \circ \tau _{k_{m-1},k_{m}}}$.

Since transpositions are odd, the sign of a cyclic permutation is length due to the concatenation property ${\displaystyle m}$

${\displaystyle \operatorname {sgn}(\sigma _{k_{1},\ldots ,k_{m}})=\operatorname {sgn}(\tau _{k_{1},k_{2}})\cdot \ldots \cdot \operatorname {sgn}(\tau _{k_{m-1},k_{m}})=(-1)^{m-1}}$.

A cyclic permutation is even if and only if its length is odd. Each permutation can now be clearly represented as a concatenation of cyclic permutations with pairwise disjoint cycles. If the lengths of these cycles are, then due to the chaining property ${\displaystyle \pi \in S_{n}}$ ${\displaystyle s\leq n}$ ${\displaystyle m_{1},\ldots ,m_{s}}$

${\displaystyle \operatorname {sgn}(\pi )=(-1)^{m_{1}-1}\cdot \ldots \cdot (-1)^{m_{s}-1}=(-1)^{m_{1}+\ldots +m_{s}-s}}$.

The sign can therefore be read directly from the cycle type of the permutation. Accordingly, a permutation is even if the sum of the lengths of the individual cycles minus the number of cycles is even. Since cycles of odd length do not change the sign, a permutation is even if the number of cycles of even length is even. Since the order of a permutation results from the smallest common multiple of its cycle length, a permutation with an odd order is always even.

example

The permutation

${\displaystyle \pi ={\begin{pmatrix}1&2&3&4&5&6\\3&6&4&1&5&2\end{pmatrix}}\in S_{6}}$

splits into three disjoint cycles, in cycle notation

${\displaystyle \pi =(1~3~4)(2~6)(5)}$.

Since the sum is odd, the permutation is also odd. Single cycles can also be omitted in the cycle notation and in the counting without changing the sum and thus the sign. ${\displaystyle 3+2+1-3}$

Representation via the determinant of the permutation matrix

Is the permutation matrix with entries belonging to the permutation ${\displaystyle P_{\pi }\in \{0,1\}^{n\times n}}$ ${\displaystyle \pi \in S_{n}}$

${\displaystyle (P_{\pi })_{ij}={\begin{cases}1,&{\text{falls }}\pi (i)=j\\0,&{\text{sonst,}}\end{cases}}}$

then corresponds to the sign of just the determinant of so ${\displaystyle \pi }$ ${\displaystyle P_{\pi }}$

${\displaystyle \operatorname {sgn}(\pi )=\det(P_{\pi })}$.

However, this representation is mostly unsuitable for the practical calculation of the sign.

example

The one for permutation

${\displaystyle \pi ={\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}\in S_{3}}$

associated permutation matrix is

${\displaystyle P_{\pi }={\begin{pmatrix}0&0&1\\1&0&0\\0&1&0\\\end{pmatrix}}}$,

whose determinant after the rule of sarrus to

${\displaystyle \det(P_{\pi })=(0+0+1)-(0+0+0)=+1}$

results.

Other properties

Powers

There are exactly different permutations of the set . For , the set of all permutations is divided into two equally large halves by the even and odd permutations, because there are equally many possibilities to choose the sign in the numerator of the product formula so that the product is positive or negative. The following applies to the power of these two sets ${\displaystyle n!}$ ${\displaystyle \{1,\ldots ,n\}}$ ${\displaystyle n\geq 2}$

${\displaystyle \#\{\pi \in S_{n}\mid \operatorname {sgn}(\pi )=+1\}=\#\{\pi \in S_{n}\mid \operatorname {sgn}(\pi )=-1\}={\frac {n!}{2}}}$.

For this reason, in addition to the sign, one speaks here of the parity (from Latin paritas , equality ) of a permutation.

Inverse permutations

For the sign of the inverse permutation of : ${\displaystyle \pi ^{-1}}$ ${\displaystyle \pi }$

${\displaystyle \operatorname {sgn}(\pi ^{-1})=\prod _{i<j}{\frac {j-i}{\pi (j)-\pi (i)}}=\prod _{i<j}{\frac {\pi (j)-\pi (i)}{j-i}}=\operatorname {sgn}(\pi )}$.

Inverting does not change the sign of a permutation, which is also directly related to the concatenation property

${\displaystyle \operatorname {sgn}(\pi ^{-1})\cdot \operatorname {sgn}(\pi )=\operatorname {sgn}(\pi ^{-1}\circ \pi )=\operatorname {sgn}(\operatorname {id} )=1}$

can be seen.

Signum homomorphism

Due to the chaining property, the figure represents

${\displaystyle \operatorname {sgn} \colon S_{n}\to \{+1,-1\}}$

represent a group homomorphism from the symmetric group to the multiplicative group (this is precisely the cyclic group of degree 2 ). This property is used in the theory of determinants, for example the Leibniz formula . The core of this homomorphism is the set of even permutations. It forms a normal divisor of , the alternating group . However, the set of odd permutations does not form a subgroup of , because the concatenation of two odd permutations results in an even permutation. ${\displaystyle (S_{n},\circ )}$ ${\displaystyle (\{+1,-1\},\cdot )}$ ${\displaystyle S_{n}}$ ${\displaystyle A_{n}}$ ${\displaystyle S_{n}}$

Conjugated permutations have the same sign as follows from the properties of sign homomorphism. Is namely , then applies to everyone ${\displaystyle \sigma \in S_{n}}$ ${\displaystyle \pi \in S_{n}}$

${\displaystyle \operatorname {sgn}(\pi \circ \sigma \circ \pi ^{-1})=\operatorname {sgn}(\pi )\cdot \operatorname {sgn}(\sigma )\cdot \operatorname {sgn}(\pi ^{-1})=\operatorname {sgn}(\pi )\cdot \operatorname {sgn}(\pi )^{-1}\cdot \operatorname {sgn}(\sigma )=\operatorname {sgn}(\sigma )}$.

use

The sign of permutations is used in the following areas, among others:

• when characterizing the determinant of a matrix using the Leibniz formula
• in the definition of antisymmetric functions , e.g. alternating multilinear forms
• in Zolotareff's lemma to represent the Legendre symbol
• in determining the achievable positions in the 15 puzzle

A very clear example can be found in the Futurama episode " In the body of the friend ". The character "Professor Farnsworth" invents a machine that swaps the souls of two people (so that the soul of person A is in the body of person B and the soul of person B is in the body of person A). Regardless of the number of exchanges made (and how many people were involved), an odd number of permutations is always necessary so that everyone is back in their own body.

generalization

A generalization of the signum for not necessarily bijective representations is the Levi-Civita symbol , which starts with the notation for like the signum about ${\displaystyle \phi \colon \{1,\ldots ,n\}\to \{1,\ldots ,n\}}$ ${\displaystyle \varepsilon _{\phi _{1}\ldots \phi _{n}}}$ ${\displaystyle \phi _{k}=\phi (k)}$ ${\displaystyle k=1,\ldots ,n}$

${\displaystyle \varepsilon _{\phi _{1}\ldots \phi _{n}}=\prod _{1\leq i<j\leq n}{\frac {\phi _{j}-\phi _{i}}{j-i}}}$

can be defined. In contrast to the Signum, the Levi-Civita-Symbol can also take on the value , which is exactly the case when the image is not bijective. The Levi-Civita symbol is used in particular in vector and tensor calculus in applications such as relativity and quantum mechanics . ${\displaystyle 0}$ ${\displaystyle \phi }$

literature

• Albrecht Beutelspacher : Linear Algebra. An introduction to the science of vectors, maps, and matrices . 6th edition. Vieweg, 2009, ISBN 3-528-56508-X .
• Siegfried Bosch : Linear Algebra . Springer, 2009, ISBN 3-540-76437-2 .

Web links

• Eric W. Weisstein : Even Permutation . In: MathWorld (English).
• Eric W. Weisstein : Odd Permutation . In: MathWorld (English).
• Raymond Puzio, Larry Hammick, Pedro Sanchez: Signature of a permutation . In: PlanetMath . (English)

Individual evidence

1. ^ Burkard Polster: The parity of permutations and the Futurama theorem. Retrieved June 21, 2019 .