Octahedral group

octahedron

Division of the spherical surface into fundamental areas according to octahedron or cube symmetry

All 13 axes of rotational symmetry of a homogeneous octahedron and the dual cube

Three 4-way axes

Four 3-way axes

Six 2-way axes

In mathematics , the octahedron group is according to convention

• the symmetry group of a homogeneous octahedron , i.e. the set of (congruence) mappings that an octahedron refers to itself, i.e. H. Map corners to corners, edges to edges, etc., or
• the rotation group of an octahedron , a subgroup of the symmetry group , in which reflections and rotational reflections are not permitted.

The full symmetry group is the direct product of the rotating group with the two-element group created by the point reflection at the center. In the second case it is also called a complete, binary or extended octahedral group to distinguish it (after Felix Klein ).

Both groups have the following figures in common as elements:

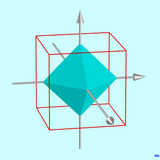
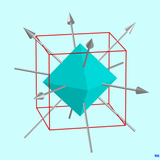
• a 90 °, 180 ° and 270 ° rotation around the three 4-fold rotation axes (through opposite corners),
• One 120 ° and one 240 ° rotation around the four 3-way axes of rotation (through opposing surface centers),
• One 180 ° rotation around the six 2-fold axes of rotation (through opposite edge centers) and
• the identity.

This results in elements of the rotating group, combined with the point mirroring results in elements of the symmetry group. All 13 axes of rotation (axes of rotational symmetry) are shown in the three graphics. The cube, which is dual to the octahedron, is drawn in as a wire frame model. ${\displaystyle 3\cdot 3+4\cdot 2+6\cdot 1+1=24}$ ${\displaystyle 2\cdot 24=48}$

The groups for octahedron and cube are isomorphic , since dual bodies have the same type of symmetry. Therefore the octahedral group can just as easily be called a cube group . The rotation groups of both bodies are isomorphic to the symmetrical group , namely to the group of permutations of the 4 threefold axes of rotation. In the case of the cube, these are the spatial diagonals and, in the case of the octahedron, the connecting lines of opposite surface centers. ${\displaystyle S_{4}}$ ${\displaystyle 4!=24}$

In crystallography , the rotation group of the octahedron is designated with the Schoenfliess symbol and the full symmetry group with . ${\displaystyle O}$ ${\displaystyle O_{h}}$

See also

• Tetrahedral group
• Icosahedral group
• polyhedron
• Platonic solid
• octahedron

literature

• Felix Klein: Lectures on the icosahedron and the solution of the equations of the fifth degree . Teubner, Leipzig 1884, p. 24 ff . (VIII, 260, online ).
• Arthur Schoenflies: Crystal systems and crystal structure . Teubner, Leipzig 1891 (XII, 638 p., Online resources ).
• John S. Lomont: Applications of finite groups . Reprint edition. Dover Publications, New York 1993, ISBN 0-486-67376-6 , pp. 81 (XI, 346 pp.). Reprint of the edition: Academic Press, New York 1959
• Harold Scott MacDonald Coxeter : Regular polytopes . 3rd ed., Unabridged and corr. repr. of the 2nd ed., New York, Macmillan, 1963. Dover Publications, New York 1973, ISBN 0-486-61480-8 , pp. 46–47 (XIII, 321 p., Limited preview in Google Book Search [accessed January 25, 2020]). The preview does not contain any page numbering.
• Frank Albert Cotton : Chemical applications of group theory . 3rd ed. Wiley, New York, NY 1990, ISBN 0-471-51094-7 , pp. 47-49 (XIV, 461 pp.).

Web links

• Octahedral Group, Mathworld
• University of Freiburg, special: octahedron. Retrieved March 7, 2020 .