Turning group

The rotation group in the narrower sense is the special orthogonal group or all rotations in real three-dimensional space (if ) or in the real plane (if ), in the latter case it is called a circle group . Its elements are the rotation matrices , i.e. orthogonal matrices with determinant one. ${\displaystyle \mathop {\mathrm {SO} } (n)}$ ${\displaystyle \mathop {\mathrm {SO} } (n,\mathbb {R} )}$ ${\displaystyle n=3}$ ${\displaystyle n=2}$

In addition, a subgroup of these real groups is referred to as a rotation group of a two- or three-dimensional figure if it includes all rotations that the figure depicts on itself, i.e. the subgroup of rotations in the symmetry group of the body or figure. To distinguish which is the full -dimensional rotation group called. ${\displaystyle \mathop {\mathrm {SO} } (n)}$ ${\displaystyle n}$

In the further and figurative sense the particular orthogonal groups - these are the sub-groups of the real general linear array ${\displaystyle \mathop {\mathrm {GL} } (n,\mathbb {R} )}$ whose elements are orthogonal matrices with determinant are one - even for higher dimensions with designated (full) as a rotary groups. ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle n>3}$

Definition and characteristics

The orthogonal group is the group of orthogonal - matrices with real elements. The connection of the orthogonal group is the matrix multiplication . The orthogonal group is a Lie group of dimension . Since the determinant of an orthogonal matrix can only take on the values , it is divided into two disjoint subsets (topologically: connected components ): ${\displaystyle \mathrm {O} (n)}$ ${\displaystyle (n\times n)}$ ${\displaystyle {\tfrac {n(n-1)}{2}}}$ ${\displaystyle \pm 1}$ ${\displaystyle \mathrm {O} (n)}$

• the rotation group of all rotations (orthogonal matrices with determinants ) and ${\displaystyle \mathrm {SO} (n)}$ ${\displaystyle +1}$
• the set of all rotational reflections (orthogonal matrices with determinants ). ${\displaystyle \mathrm {O} (n)\setminus \mathrm {SO} (n)}$ ${\displaystyle -1}$

The subgroup is called the special orthogonal group or the rotating group. ${\displaystyle \mathrm {SO} (n)}$

In particular, as the group of all rotations about an axis running through the coordinate origin in three-dimensional space, it is of great importance in numerous applications, such as computer graphics or physics. ${\displaystyle \mathrm {SO} (3)}$

Two-dimensional rotations

→ Main article : Kreisgruppe

The circle group is the Lie group, which summarizes the rotations around a fixed point in two-dimensional space (a plane) and describes the execution of these rotations one after the other. Such a rotation can be clearly described by an angle, the execution of two rotations one after the other corresponds to the rotation around the sum of the two angles of the individual rotations. A full turn is again identified with no turn. ${\displaystyle SO(2)\cong S^{1}}$

Three-dimensional rotations

Eulerwinkel and : The blue tripod should be converted into the red one. If you transfer the red and the blue x-axis to the green "node line" by rotating around the respective z-axis, all that is missing is a rotation around the green axis. ${\displaystyle \alpha ,\beta }$ ${\displaystyle \gamma }$

Description by axis and angle

A rotation in three-dimensional space can be described by specifying an axis of rotation, i.e. a vector of length one on the unit sphere , and an angle of rotation . In a special case , the image is identical; for other angles, also in the case of a straight line mirroring , the axis is clearly defined. By changing the orientation of the axis of rotation, a rotation about can also be understood as a rotation with an angle . ${\displaystyle v\in S^{\,2}}$ ${\displaystyle \varphi \in [0;2\pi [}$ ${\displaystyle \varphi =0}$ ${\displaystyle \varphi =\pi }$ ${\displaystyle \varphi }$ ${\displaystyle 2\pi -\varphi }$

The associated rotation can be specified explicitly by an associated rotation matrix (see there). ${\displaystyle D(v,\varphi )}$

Description by Euler's angle

To Leonhard Euler another description goes from rotations about three angles, the so-called Euler angles back. Starting from the standard basis , Euler showed that any rotation turns out to be ${\displaystyle e_{x},\,e_{y},\,e_{z}}$ ${\displaystyle D}$

${\displaystyle D=D(e_{z},\alpha )\circ D(e_{x},\beta )\circ D(e_{z},\gamma )}$

lets write.

In this case, the three angles are subject to the limitation uniquely determined up to singular areas: Approximately for sufficient one of the two other angle. ${\displaystyle \beta \in [-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}}[}$ ${\displaystyle \beta =0}$

Euler's angles are often used in physics ; for example, the description of the orbits of planets or asteroids by the so-called orbital elements is based on it.

Description using quaternions

${\displaystyle \times }$	${\displaystyle 1}$	${\displaystyle {\rm {i}}}$	${\displaystyle {\rm {j}}}$	${\displaystyle {\rm {k}}}$
${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle {\rm {i}}}$	${\displaystyle {\rm {j}}}$	${\displaystyle {\rm {k}}}$
${\displaystyle {\rm {i}}}$	${\displaystyle {\rm {i}}}$	${\displaystyle -1}$	${\displaystyle {\rm {k}}}$	${\displaystyle -{\rm {j}}}$
${\displaystyle {\rm {j}}}$	${\displaystyle {\rm {j}}}$	${\displaystyle -{\rm {k}}}$	${\displaystyle -1}$	${\displaystyle {\rm {i}}}$
${\displaystyle {\rm {k}}}$	${\displaystyle {\rm {k}}}$	${\displaystyle {\rm {j}}}$	${\displaystyle -{\rm {i}}}$	${\displaystyle -1}$

The Hamiltonian quaternions allow a very elegant description of spatial rotations. The quaternions form a four-dimensional algebra over the real numbers. Four special quaternions are used as a basis, namely and . Here (ie the multiplication is not commutative) and apply the following of William Rowan Hamilton specified calculation rules: . With this multiplication rule - different, mathematically exact constructions of the quaternion algebra can be found here - even becomes an inclined body : For each quaternion different from zero an inverse quaternion can be calculated, for which applies. ${\displaystyle \mathbb {H} }$ ${\displaystyle 1,{\rm {i,{\rm {j}}}}}$ ${\displaystyle {\rm {k}}}$ ${\displaystyle {\rm {k={\rm {i\cdot {\rm {j=-{\rm {j\cdot {\rm {i}}}}}}}}}}}$ ${\displaystyle {\rm {i^{2}={\rm {j^{2}={\rm {k^{2}=-1}}}}}}}$ ${\displaystyle \mathbb {H} }$ ${\displaystyle q}$ ${\displaystyle q^{-1}}$ ${\displaystyle q\cdot q^{-1}=1=q^{-1}\cdot q}$

A quaternion is called pure if it can be written as a linear combination of the three basis vectors and . Ability of linear embedding ${\displaystyle {\rm {i,{\rm {j}}}}}$ ${\displaystyle {\rm {k}}}$

${\displaystyle \mathbb {R} ^{3}\ni v\mapsto {\hat {v}}\in \mathbb {H} }$

with , and let's identify the one with the pure quaternions. Now the multiplication rule for quaternions can be interpreted geometrically: The product of two pure quaternions and is not pure again, but it holds ${\displaystyle {\hat {e}}_{x}={\rm {i}}}$ ${\displaystyle {\hat {e}}_{y}={\rm {j}}}$ ${\displaystyle {\hat {e}}_{z}={\rm {k}}}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle {\hat {v}}}$ ${\displaystyle {\hat {w}}}$

${\displaystyle {\hat {v}}\cdot {\hat {w}}=-\ v\cdot w\cdot 1+{\widehat {v\times w}}}$

The pure part of the product of two pure quaternions corresponds to their cross product , while the scalar part (the coefficient in front of the basis vector ) represents the negative of their scalar product . ${\displaystyle 1}$

In order to describe the rotation through a quaternion, we first need an angle whose double corresponds to the given one. Besides does this too . We now consider the quaternion ${\displaystyle D(v,\varphi )}$ ${\displaystyle \psi }$ ${\displaystyle 2\psi ,}$ ${\displaystyle \varphi }$ ${\displaystyle \psi ={\tfrac {\varphi }{2}}}$ ${\displaystyle \psi ={\tfrac {\varphi }{2}}+\pi }$

${\displaystyle q:=\cos \psi +{\hat {v}}\cdot \sin \psi }$

This quaternion is length one (with respect to the standard scalar product in ) and its inverse is ${\displaystyle \mathbb {R} ^{4}}$

${\displaystyle q^{-1}=\cos \psi -{\hat {v}}\cdot \sin \psi }$

If one now takes any pure quaternion , it can easily be shown that the quaternion conjugated with ${\displaystyle {\hat {x}}}$ ${\displaystyle q}$

${\displaystyle {\hat {y}}:=q\cdot {\hat {x}}\cdot q^{-1}}$

is again a pure quaternion (whereby it can only be represented as for exactly one ). The following now applies ${\displaystyle {\hat {y}}}$ ${\displaystyle y\in \mathbb {R} ^{3}}$

${\displaystyle y=D(v,\varphi )(x)}$

In other words: the conjugation with acts on the pure quaternions like the rotation . ${\displaystyle q}$ ${\displaystyle D(v,\varphi )}$

Universal overlay of the SO (3)

A two-leaf overlay: Shown here using the example of the complex square root. Exactly two points of the overlying space lie above each point of the dotted complex number plane. For a complex number , exactly two numbers can be found with . When drawing in three-dimensional space, self-penetration of the surface is unavoidable. ${\displaystyle z\neq 0}$ ${\displaystyle w}$ ${\displaystyle w^{2}=z}$

The ambiguity observed above in the choice of goes hand in hand with the two possible vectors for describing the axis: A specific rotation can be precisely described by two unit quaternions that are inverse to one another. In purely topological terms, the set of unit quaternions is obviously the three-dimensional unit sphere in four-dimensional space. The quaternion multiplication gives it a Lie group structure. As such, it is isomorphic to the particular unitary group . As discussed in the previous section, conjugation with a unit quaternion provides a rotation. Obviously this is a surjective group homomorphism, which shows a diffeomorphism on its image in a sufficiently small area . In other words, the picture ${\displaystyle \psi }$ ${\displaystyle \mathrm {Spin} (3)\subset \mathbb {H} }$ ${\displaystyle S^{\,3}\subset \mathbb {R} ^{4}\cong \mathbb {H} }$ ${\displaystyle \mathrm {SU} (2)}$ ${\displaystyle q\in \mathrm {Spin} (3)}$ ${\displaystyle q}$ ${\displaystyle \mathrm {SO} (3)}$

${\displaystyle \mathrm {Spin} (3)\rightarrow \mathrm {SO} (3)}$

is a two-leaf overlay . Since is simply connected , it is about the universal superposition of the . ${\displaystyle \mathrm {Spin} (3)=S^{\,3}}$ ${\displaystyle \mathrm {SO} (3)}$

To understand the vivid meaning of this universal overlay, let us consider the theorem of football . With suitable markings on the ball, the rotation that the ball has made since it was kicked can in principle be determined at any point in time. This gives a steady path through that starting at the identity matrix. Describing the unit matrix as by the unit element of (alternatively could be the antipodal opposing member in so use), so now the entire path can be in a continuous manner to a path through the lift. Even if at the beginning of the second half the ball is positioned exactly the same way on the point of impact according to the markings (the path through the ends again at the point of the identity matrix), it is not guaranteed that the lifted path will return to the one Quaternion has arrived. With a probability of 50%, the latter ends in the ; then you would have to turn the ball again by 360 ° with respect to any chosen axis in order to let the lifted path end in its starting point. Since there is no higher-leaved overlay of the , it is not possible to consistently grasp the general rotations in space even more finely. ${\displaystyle \mathrm {SO} (3)}$ ${\displaystyle \mathrm {Spin} (3)}$ ${\displaystyle \mathrm {Spin} (3)=S^{\,3},}$ ${\displaystyle -1\in \mathbb {H} }$ ${\displaystyle \mathrm {Spin} (3)}$ ${\displaystyle \mathrm {SO} (3)}$ ${\displaystyle 1\in \mathbb {H} }$ ${\displaystyle -1}$ ${\displaystyle \mathrm {SO} (3)}$

Remarkably, in quantum mechanics one uses the and not the as a state space to describe the spin of a particle. ${\displaystyle \mathrm {SU} (2)}$ ${\displaystyle \mathrm {SO} (3)}$

Topology of the SO (3)

Each fiber of the overlay just described

${\displaystyle S^{\,3}\to \mathrm {SO} (3)}$

consists of two antipode points (corresponding to the two options for choosing with ) the . Consequently, the is homeomorphic to the quotient of when opposing points are identified . However, this results exactly in the three-dimensional real projective space . ${\displaystyle \psi }$ ${\displaystyle 2\psi =\varphi \,\mathrm {mod} \,2\pi \mathbb {Z} }$ ${\displaystyle S^{\,3}}$ ${\displaystyle \mathrm {SO} (3)}$ ${\displaystyle S^{\,3}}$ ${\displaystyle \mathbb {R} P^{3}}$

Finite subgroups of the SO (3)

When a spin gets the cube, it also gets the dual octahedron.

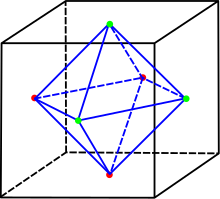
The finite subgroups of are closely related to spatial bodies that have a finite number of symmetries. Since for any rotation of a cube in space, the associated subgroup is conjugated with this rotation, we are only interested in the conjugation classes of the finite subgroups of . These are: ${\displaystyle \mathrm {SO} (3)}$ ${\displaystyle \mathrm {SO} (3)}$

• The cyclic groups for , generated by a rotation of the -th part of a full angle ; for they are part of the full rotating group of a straight prism over a regular corner. ${\displaystyle C_{n}}$ ${\displaystyle n\geq 1}$ ${\displaystyle n}$ ${\displaystyle 2\pi }$ ${\displaystyle n\geq 3}$ ${\displaystyle n}$
• The full rotating group of such a prism. In addition to the one already described, it also contains those rotations that act like axis reflections on the regular corner, but which turn into rotations of the room through simultaneous mirroring on the carrier plane of the corner. These are the dihedral groups of the order (formal for ; geometric interpretation for ). ${\displaystyle C_{n}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle D_{n}}$ ${\displaystyle 2n}$ ${\displaystyle n\geq 2}$ ${\displaystyle n\geq 3}$
• The full rotation group of a regular tetrahedron . It is isomorphic to the alternating group of the order . ${\displaystyle \mathbb {T} }$ ${\displaystyle A_{4}}$ ${\displaystyle 12}$
• The full rotating group of a regular octahedron , the so-called octahedron group of order . It is also responsible for the cube that is dual to the octahedron. It is isomorphic to the symmetric group . ${\displaystyle \mathbb {O} }$ ${\displaystyle 24}$ ${\displaystyle S_{4}}$
• The full rotating group of a regular icosahedron (see icosahedron group ) of the order . It also describes the rotations of the dodecahedron and is isomorphic to the alternating group . ${\displaystyle \mathbb {I} }$ ${\displaystyle 60}$ ${\displaystyle A_{5}}$

Rotating groups of figures

The word rotation group is also used as a designation for that subgroup of the symmetries of a certain geometrical object that depicts a planimetric figure or a stereometric body on itself by rotation. Such a rotation group is then a (mostly finite) subgroup of the or the and consists precisely of all those rotations through which this figure or this body is transformed into itself. ${\displaystyle \mathrm {SO} _{2}(\mathbb {R} )}$ ${\displaystyle \mathrm {SO} _{3}(\mathbb {R} )}$

Examples

• in the plane

1. The rotation group of a line corresponds to its symmetry group and consists of only two elements: the identity and the rotation by 180 ° around the center. So it is isomorphic to the symmetric group . ${\displaystyle S_{2}}$
2. The rotation group of a regular polygon with corners is isomorphic to the cyclic group . This is a normal divisor of the associated symmetry group, the dihedral group . ${\displaystyle n}$ ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$ ${\displaystyle D_{n}}$

• in three-dimensional space

1. The rotation group of the tetrahedron , a subgroup of the tetrahedron group , contains 12 elements (rotations around 3 and 2-fold axes) and is isomorphic to the alternating group ${\displaystyle A_{4}}$ on the set of four corners. Her Schoenflies symbol is . ${\displaystyle T}$
2. The rotation group of the octahedron and that of the dual cube , a subgroup of the octahedron group , contains 24 elements (rotations around 4, 3 and 2-fold axes) and is isomorphic to the symmetrical group on the set of the four 3-fold axes. Her Schoenflies symbol is . ${\displaystyle S_{4}}$ ${\displaystyle O}$
3. The rotation group of the icosahedron and that of the dodecahedron dual to it , a subgroup of the icosahedron group , contains 60 elements (rotations around 5, 3 and 2-fold axes) and is isomorphic to the alternating group . Her Schoenflies symbol is . ${\displaystyle A_{5}}$ ${\displaystyle I}$

Applications

• Theorem of football - illustrative application of the rotating group . ${\displaystyle \mathrm {SO} (3)}$

literature

• Theodor Bröcker , Tammo tom Dieck : Representations of Compact Lie Groups (= Graduate Text in Mathematics. Volume 98). Springer, New York NY a. a. 1985, ISBN 3-540-13678-9 .
• Horst Knörrer : Geometry (= Vieweg study. Volume 71). Vieweg, Braunschweig a. a. 1996, ISBN 3-528-07271-7 .
• Uwe Storch , Hartmut Wiebe: Textbook of Mathematics. Volume 2: Linear Algebra. BI-Wissenschafts-Verlag, Mannheim 1990, ISBN 3-411-14101-8 .

Individual evidence

1. ↑ It is a real multiple of . ${\displaystyle (a+b\mathrm {i} +c\mathrm {j} +d\mathrm {k} )\cdot (a-b\mathrm {i} -c\mathrm {j} -d\mathrm {k} )=a^{2}+b^{2}+c^{2}+d^{2}}$ ${\displaystyle 1}$
2. ^ Bröcker, tom Dieck: Representations of Compact Lie Groups. 1985, p. 7.
3. ^ Bröcker, tom Dieck: Representations of Compact Lie Groups. 1985, p. 60 f.
4. ↑ See Knörrer: Geometry. 1996, p. 47.