100 prisoners problem

Every prisoner has to find his number in one of 100 drawers, but is only allowed to open 50 of the drawers.

The 100 prisoners problem is a mathematical problem from probability theory and combinatorics . With this problem, each of 100 numbered prisoners has to find their own number in one of 100 drawers in order to survive, whereby each prisoner is only allowed to open 50 of the drawers and not communicate with the other prisoners. In this seemingly hopeless situation, there is nevertheless a strategy that gives the prisoners a good chance of survival. The problem was first introduced in 2003 by the Danish computer scientist Peter Bro Miltersen.

Problem

There are different representations in the literature for the problem of the 100 prisoners. The following formulation of the problem is based on a description by Philippe Flajolet and Robert Sedgewick :

“The head of a prison gives 100 death row prisoners numbered 1 to 100 one last chance. In one room there is a cabinet with 100 drawers. The prison director puts the number of exactly one prisoner in each drawer in random order and then closes the drawers. The prisoners enter the room one after the other. Each prisoner is allowed to open 50 drawers in any order and must then close them again with their contents. If all prisoners find their own number in one of the drawers, the prisoners are pardoned. If any prisoner does not find his number, all prisoners must die. Before the first prisoner enters the room, the prisoners are allowed to consult, but after that no communication is possible. What is the best strategy for the prisoners? "

If each prisoner chooses his 50 drawers at random , then the probability that a single prisoner will find his number is 50 percent. The probability that all prisoners will find their numbers is then equal to the product of the individual probabilities and thus 0.5 ¹⁰⁰ ≈ 10 ^−30.1 ≈ 8 · 10 ⁻³¹ = 0.0000000000000000000000000000008, i.e. H. with less than 1: 1 quintillion vanishingly small. The situation seems hopeless for the prisoners.

solution

strategy

However, there is a strategy that will give prisoners a little over 30% chance of survival. The key to success is that prisoners don't have to decide in advance which drawers to open. When deciding which drawer to open next, every prisoner can rely on the information he has received from the drawers he has already opened. Another important observation is that the success of one prisoner is not independent of the success of the other prisoners.

First, the prisoners mentally number the drawers with numbers from 1 to 100, for example line by line from top left to bottom right. The strategy is now as follows:

The first thing each prisoner does is open the drawer with his own number.
If his number is in this drawer, then he has finished the search and was successful.
Otherwise there will be another prisoner's number in the drawer and he will next open the drawer with that number.
The prisoner repeats steps 2 and 3 until he finds his own number or until he has opened 50 drawers.

Without the restriction to 50 drawers, this procedure would in any case result in a cycle of numbers that begins and ends with the prisoner's number. If this cycle consists of up to 50 numbers, the prisoner was successful; otherwise it failed.

Examples

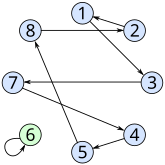
The following example with eight prisoners and drawers, whereby each prisoner is allowed to open four drawers, is to illustrate that this strategy is promising. The prison director had distributed the prisoners' numbers on the drawers as follows:

Number of the drawer	1	2	3	4th	5	6th	7th	8th
Prisoner number	7th	4th	6th	8th	1	3	5	2

The prisoners now act as follows:

Prisoner 1 opens drawer 1 and finds number 7. Thereupon he opens drawer 7 and finds number 5. Now he opens drawer 5, finds his own number 1 there and is therefore successful.
Prisoner 2 opens drawers 2, 4 and 8 in that order, finding his own number 2 in drawer 8.
Prisoner 3 opens drawers 3 and 6, where he already finds his own number.
Prisoner 4 opens drawers 4, 8 and 2, where he then finds his own number. This can also be deduced from the information that the second prisoner received.
That prisoners 5 to 8 will also find their numbers can also be deduced from the information of the first three prisoners.

In this case, the prisoners will successfully find all their numbers. However, this is not always the case. As a second example, the prison director has now distributed the numbers as follows:

Number of the drawer	1	2	3	4th	5	6th	7th	8th
Prisoner number	3	1	7th	5	8th	6th	4th	2

In this case, prisoner 1 opens drawers 1, 3, 7 and 4 in the row, where he has to break off without success. Except for prisoner 6, who can find his number directly, all other prisoners would also be unsuccessful.

Permutation representation


Graphs of the permutations and ${\ displaystyle (1 ~ 7 ~ 5) (2 ~ 4 ~ 8) (3 ~ 6)}$ ${\ displaystyle (1 ~ 3 ~ 7 ~ 4 ~ 5 ~ 8 ~ 2) (6)}$

The random assignment of prisoners to drawers made by the prison director can be described mathematically as a permutation of the numbers from 1 to 100. Such a permutation is a clearly reversible mapping of the set of natural numbers from 1 to 100 in itself. A sequence of numbers that results from repeated application of a permutation and at the end returns to the original number is called the cycle of permutation. Each permutation breaks down into disjoint cycles consisting of different numbers and can be described by its cycle type . The first example permutation of the previous section can be written in cycle notation through

{\ displaystyle (1 ~ 7 ~ 5) (2 ~ 4 ~ 8) (3 ~ 6)}

and thus consists of two cycles of length three and one cycle of length two. The second example permutation has the representation

{\ displaystyle (1 ~ 3 ~ 7 ~ 4 ~ 5 ~ 8 ~ 2) (6)}

and consists of one cycle of length seven and one of length one. The cycle representation is not clear, because a cycle of length can be written in different ways by choosing a different start number. Each prisoner now follows a cycle when opening the drawer, which ends with his own number. With eight prisoners, this cycle sequence strategy is successful for any permutation if and only if the length of the longest cycle of the permutation is at most four. If the permutation has a cycle of length five or more, then all prisoners whose numbers are in this cycle will not have reached their own number after four steps. ${\ displaystyle l}$ ${\ displaystyle l}$

Probability of success

Probability distribution of the length of the longest cycle of a random permutation of the numbers from 1 to 100. The green area corresponds to the survival probability of the prisoners.

Applied to the original problem of 100 prisoners, their strategy will be successful if and only if the longest cycle of the permutation has a length of 50 or less. The probability that the prisoners will survive is thus equal to the probability that a random permutation of the numbers from 1 to 100 does not contain a cycle with a length greater than 50. This probability is determined below.

First, a permutation of the numbers from 1 to 100 can have a maximum of one cycle with one length . There are exactly possibilities to select the numbers of such a cycle (see combination without repetition ). These numbers can be arranged in ways within the cycle (see permutation without repetition ), because there are options to select the starting number of the cycle. Finally, the remaining numbers can be arranged in ways. So the number of permutations of the numbers from 1 to 100 with one cycle of length is the same ${\ displaystyle l> 50}$ ${\ displaystyle {\ tbinom {100} {l}}}$ ${\ displaystyle (l-1)!}$ ${\ displaystyle l}$ ${\ displaystyle (100-l)!}$ ${\ displaystyle l> 50}$

{\ displaystyle {\ binom {100} {l}} \ cdot (l-1)! \ cdot (100-l)! = {\ frac {100!} {l}}}

.

The harmonic numbers result approximately as the area under the hyperbola and can thus be approximated using the logarithm function.

The probability that a ( uniformly distributed ) random permutation does not have a cycle with a length greater than 50 is accordingly with the formula for the opposite probability and the Laplace formula

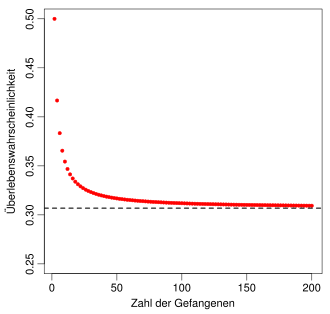
{\ displaystyle 1 - {\ frac {1} {100!}} \ left ({\ frac {100!} {51}} + \ ldots + {\ frac {100!} {100}} \ right) = 1 - \ left ({\ frac {1} {51}} + \ ldots + {\ frac {1} {100}} \ right) = 1- (H_ {100} -H_ {50}) \ approx 0 {, } 31183}

,

where is the -th harmonic number . The probability that the prisoners survive is an astonishing 31% with the cycle-following strategy. ${\ displaystyle H_ {n}}$ ${\ displaystyle n}$

Consideration of limit values

Probability of survival as a function of the number of prisoners

If prisoners are generally considered instead of 100 prisoners , where any natural number is, then the probability of survival with the cycle-following strategy is ${\ displaystyle 2n}$ ${\ displaystyle n}$

{\ displaystyle 1- (H_ {2n} -H_ {n}) = 1- (H_ {2n} - \ ln 2n) + (H_ {n} - \ ln n) - \ ln 2}

.

With the Euler-Mascheroni constant we now have for ${\ displaystyle \ gamma}$ ${\ displaystyle n \ to \ infty}$

{\ displaystyle \ lim _ {n \ to \ infty} (H_ {n} - \ ln n) = \ gamma}

,

which results in an asymptotic survival probability of

{\ displaystyle \ lim _ {n \ to \ infty} (1-H_ {2n} + H_ {n}) = 1- \ gamma + \ gamma - \ ln 2 = 1- \ ln 2 \ approx 0 {,} 30685}

results. Since the sequence of the probabilities is monotonically falling , the prisoners with the cycle-following strategy survive with any number of prisoners in more than 30% of the cases.

Optimality

In 2006, Eugene Curtin and Max Warshauer gave proof of the optimality of the cycle following strategy. The evidence is based on making an equivalence to a related problem where all prisoners are allowed to be in the room and watch the selection of drawers. This equivalence is based on a correspondence between the (normalized) cycle notation and the tuple representation of permutations. In the second problem, the probability of success is independent of the strategy chosen and is the same as the probability of success in the initial problem with the cycle sequence strategy. Since any strategy for the initial problem can also be used in the second problem, but has no higher probability of success there, the cycle sequence strategy must be optimal.

history

The problem of 100 prisoners was first considered in 2003 by the Danish computer scientist Peter Bro Miltersen and published with Anna Gál in a conference contribution to the 30th International Colloquium on Automata, Languages and Programming (ICALP). In their version, player A (the prison chief) colors notes with the names of the players from team B (the prisoners) red or blue and puts them in a box. For the team to win, each player on team B must correctly guess the color of their slip of paper after opening half of the boxes. Initially, Miltersen assumed that the probability of winning tends to zero very quickly with the number of players. However, Sven Skyum, a colleague of Miltersen at Aarhus University , drew his attention to the cycle-following strategy. Finding this strategy was left open as an exercise in the conference contribution. The contribution was awarded the Best Paper Award .

The problem appeared in the spring 2004 puzzle column by Joe Buhler and Elwyn Berlekamp in The Emissary of the Mathematical Sciences Research Institute , replacing boxes with permanent memories and colored pieces of paper with signed numbers. The authors found that the probability of winning can also be increased in the event that the team members cannot find their own number during the cycle sequence. In this case, if the answer is the product of all signs found and the length of the longest cycle is one greater than half the (even) number of players, then the team members who find themselves in this cycle guess either all correctly or all not correct. While this expansion of strategy gives a visible improvement in a small number of players, it becomes negligible as the number of players increases.

In the following years the problem found its way into the mathematical literature, where it was lined up in different ways, for example with cards hidden on a table or wallets in lockers (loose puzzle) . In the form of a prisoner problem, it was then posed in 2006 by Christoph Pöppe in the journal Spektrum der Wissenschaft and by Peter Winkler in the College Mathematics Journal . With slight modifications it was adopted in this form by, among others, Philippe Flajolet, Robert Sedgewick and Richard P. Stanley in their textbooks on combinatorics.

variants

Empty boxes

In their conference contribution, Gál and Miltersen first considered the case that the number of boxes is twice as large as the number of team members, with half of the boxes being empty. This is a more difficult problem because empty boxes don't go anywhere and the cycle following strategy cannot be used here. It is an open question whether in this case the probability of winning tends to zero for a growing number of team members.

In 2005, Navin Goyal and Michael Saks developed a strategy for team B based on the cycle sequence strategy for a more general problem in which both the proportion of empty boxes and the proportion of boxes that each team member is allowed to open vary. In this case, the probability of winning still tends to zero as the number of players increases, but less quickly than assumed by Gál and Miltersen. If the number of players and the proportion of boxes to be opened are fixed, the probability of winning really remains greater than zero if more empty boxes are added.

In 2009, David Avis and Anne Broadbent looked at a quantum IT variant in which Team B will definitely win.

The malicious head of the prison

In the event that the prison chief does not have to put the prisoners 'numbers in the drawers in a random order, he can override the prisoners' strategy with knowledge of the numbering of the drawers. To do this, he only has to ensure that his assignment of the numbers to the drawers represents a permutation with a cycle of length greater than 50. However, the prisoners can restore their original probability of winning by randomly numbering the drawers.

Goat problem

Adam S. Landsberg suggested the following simplified variant of the problem in 2009, which is based on the well-known goat problem (Monty Hall problem):

“Behind three locked doors there is a randomly distributed car, the car keys and a goat. There are two players: the first player has to find the car, the second player the car keys. Only if both players are successful are they allowed to drive home. First the first player enters the room and is allowed to open two of the three doors one after the other. If he is successful, the doors are closed again and the second player enters the room. The second player may also open two of the three doors, but cannot communicate in any way with the first player. What is the probability of winning if both players act optimally? "

If the two players choose the doors at random, the probability of winning is only 4/9 (around 44%). However, the optimal strategy is as follows:

Player 1 first opens door 1. If the car is in it, he is successful. If the keys are in it, he opens door 2 next, otherwise door 3.
Player 2 first opens door 2. If the keys are in it, he is successful. If the goat is inside, he opens door 3 next, otherwise door 1.

With the six possible distributions of car, key and goat to the three doors, the players then open the following doors (if a field has a green background, the respective player was successful):

	Car - Key - Goat	Car - goat - key	Key - car - goat	Key - goat - car	Goat - car - key	Goat - key - car
Player 1	Door 1: car	Door 1: car	Door 1: Key Door 2: Car	Door 1: Key Door 2: Goat	Door 1: goat Door 3: key	Door 1: goat Door 3: car
Player 2	Door 2: key	Door 2: goat Door 3: key	Door 2: Car Door 1: Key	(Door 2: goat) (door 3: car)	(Door 2: car) (door 1: goat)	Door 2: key

The success of the strategy apparently consists in establishing a correlation between the successes and failures of the two players. The probability of winning in this case is 2/3 and is optimal, since the first player does not have a higher probability of success. Another variant is to hide three prizes behind the three doors and let three players independently find a different, predetermined price with two attempts. Here, too, the probability of winning is 2/3 with an optimal strategy.

literature

Philippe Flajolet , Robert Sedgewick : Analytic Combinatorics . Cambridge University Press, 2009, ISBN 978-1-139-47716-1 .
Richard P. Stanley : Algebraic Combinatorics: Walks, Trees, Tableaux, and More (= Undergraduate Texts in Mathematics ). Springer, 2013, ISBN 978-1-4614-6998-8 .
Peter Winkler: Mathematical Mind-Benders . Taylor and Francis, 2007, ISBN 978-1-56881-336-3 .

Web links

100 prisoners - a stochastic problem . ( Memento of March 16, 2016 in the Internet Archive ) April 18, 2009.
Rob Heaton: Mathematicians hate civil liberties - 100 prisoners and 100 boxes . January 13, 2014 (English).
Oliver Nash: Pity the prisoners . December 12, 2009 (English).
Jamie Mulholland: Prisoners Names in Boxes . ( Memento of March 4, 2016 in the Internet Archive ) 2011 (PDF; 204 kB; English).
MinutePhysics: An Impossible Bet on YouTube and Solution to The Impossible Bet on YouTube , December 8, 2014 (English).
Edmund Weitz ( HAW Hamburg ): The problem of 100 prisoners on YouTube , April 21, 2018.
Matt Parker (standupmaths) and Alex Bellos : The unbelievable solution to the 100 prisoner puzzle on YouTube , November 4, 2019 (English).

Individual evidence

^ ^A ^b Philippe Flajolet, Robert Sedgewick: Analytic Combinatorics . Cambridge University Press, 2009, pp. 124 .
↑ ^a ^b ^c ^d Eugene Curtin, Max Warshauer: The locker puzzle . In: Mathematical Intelligencer . No. 28 , 2006, pp. 28-31 , doi : 10.1007 / BF02986999 .
↑ ^a ^b ^c ^d Richard P. Stanley: Algebraic Combinatorics: Walks, Trees, Tableaux, and More . Springer, 2013, p. 187-189 .
↑ ^a ^b Anna Gál, Peter Bro Miltersen: The cell probe complexity of succinct data structures . In: Proceedings 30th International Colloquium on Automata, Languages and Programming (ICALP) . 2003, p. 332-344 .
^ Joe Buhler, Elwyn Berlekamp: Puzzles Column . In: The Emissary . Jump. Mathematical Sciences Research Institute, 2004, pp. 3 ( msri.org ).
↑ Richard E. Blahut: Cryptography and Secure Communication . Cambridge University Press, 2014, pp. 29-30 .
↑ Christoph Pöppe: freedom for the Combinatorial Riker. Math conversations . In: Spectrum of Science . tape 6 , 2006, p. 106-108 ( Spektrum.de ).
↑ Peter Winkler: Names in Boxes Puzzle . In: College Mathematics Journal . tape 37 , no. 4 , 2006, p. 260, 285, 289 .
↑ Navin Goyal, Michael Saks: A parallel search game . In: Random Structures & Algorithms . tape 27 , no. 2 , 2005, p. 227-234 .
↑ David Avis, Anne Broadbent: The quantum locker puzzle . In: Third International Conference on Quantum, Nano and Micro Technologies ICQNM '09 . 2009, p. 63-66 .
^ Philippe Flajolet, Robert Sedgewick: Analytic Combinatorics . Cambridge University Press, 2009, pp. 177 .
^ ^A ^b Adam S. Landsberg: The Return of Monty Hall . In: Mathematical Intelligencer . tape 31 , no. 2 , 2009, doi : 10.1007 / s00283-008-9016-8 .
↑ Eric Grundwald: Re: The Locker Puzzle . In: Mathematical Intelligencer . tape 32 , no. 2 , 2010, doi : 10.1007 / s00283-009-9107-1 .

[flajolet-1] A ^b Philippe Flajolet, Robert Sedgewick: Analytic Combinatorics . Cambridge University Press, 2009, pp. 124 .

[curtin-2] Eugene Curtin, Max Warshauer: The locker puzzle . In: Mathematical Intelligencer . No. 28 , 2006, pp. 28-31 , doi : 10.1007 / BF02986999 .

[stanley-3] Richard P. Stanley: Algebraic Combinatorics: Walks, Trees, Tableaux, and More . Springer, 2013, p. 187-189 .

[miltersen-4] Anna Gál, Peter Bro Miltersen: The cell probe complexity of succinct data structures . In: Proceedings 30th International Colloquium on Automata, Languages and Programming (ICALP) . 2003, p. 332-344 .

[buhler-5] Joe Buhler, Elwyn Berlekamp: Puzzles Column . In: The Emissary . Jump. Mathematical Sciences Research Institute, 2004, pp. 3 ( msri.org ).

[6] Richard E. Blahut: Cryptography and Secure Communication . Cambridge University Press, 2014, pp. 29-30 .

[pöppe-7] Christoph Pöppe: freedom for the Combinatorial Riker. Math conversations . In: Spectrum of Science . tape 6 , 2006, p. 106-108 ( Spektrum.de ).

[winkler-8] Peter Winkler: Names in Boxes Puzzle . In: College Mathematics Journal . tape 37 , no. 4 , 2006, p. 260, 285, 289 .

[9] Navin Goyal, Michael Saks: A parallel search game . In: Random Structures & Algorithms . tape 27 , no. 2 , 2005, p. 227-234 .

[10] David Avis, Anne Broadbent: The quantum locker puzzle . In: Third International Conference on Quantum, Nano and Micro Technologies ICQNM '09 . 2009, p. 63-66 .

[11] Philippe Flajolet, Robert Sedgewick: Analytic Combinatorics . Cambridge University Press, 2009, pp. 177 .

[landsberg-12] A ^b Adam S. Landsberg: The Return of Monty Hall . In: Mathematical Intelligencer . tape 31 , no. 2 , 2009, doi : 10.1007 / s00283-008-9016-8 .

[13] Eric Grundwald: Re: The Locker Puzzle . In: Mathematical Intelligencer . tape 32 , no. 2 , 2010, doi : 10.1007 / s00283-009-9107-1 .