Predicate logic
The predicate logics (also quantifier logics ) form a family of logical systems that make it possible in practice and in the theory of many sciences to formalize important areas by means of arguments and to check their validity. Because of this property, predicate logic plays a major role in logic as well as in mathematics , computer science , linguistics and philosophy .
Gottlob Frege and Charles Sanders Peirce independently developed predicate logic. Frege developed and formalized his system in the term writing published in 1879 . Older logical systems, for example traditional conceptual logic , are real subsets of predicate logic in terms of their expressiveness. They can be fully translated into this.
Central terms
Predicate logic is an extension of propositional logic . In propositional logic, compound statements are examined to determine which simpler statements are made up of them. For example, the statement “It's raining or the earth is flat” consists of the two statements “It's raining” and “The earth is flat”. These two statements themselves cannot be broken down into further sub-statements - they are therefore called atomic or elementary. In predicate logic, atomic statements are examined with regard to their internal structure.
A central concept of predicate logic is the predicate . A predicate is a series of words with spaces that become true or false if a proper name is inserted into each space. For example, the word sequence "... is a person" is a predicate because inserting a proper name - such as "Socrates" - creates a statement such as "Socrates is a person". The statement “The earth is a disk” can be broken down into the proper name “the earth” and the predicate “... is a disk”. On the basis of the definition and the examples it becomes clear that the term “predicate” in logic, especially in predicate logic, does not have the same meaning as in grammar , even if there is a historical and philosophical connection. Instead of a proper name, a variable can be inserted into the predicate, whereby the predicate becomes a sentence function: φ ( x ) = " x is a person" is a function that is used in classical predicate logic for the proper names of those individuals who are people , outputs the truth value true and for all others the truth value false .
The second characteristic concept of predicate logic is the quantifier . Quantifiers indicate by how many individuals in the discourse universe a sentence function is fulfilled. A quantifier binds the variable of a sentence function so that another sentence is created. The universal quantifier states that a predicate should apply to all individuals. The existential quantifier says that a predicate applies to at least one individual. The quantifiers enable statements such as “All people are mortal” or “There is at least one pink elephant”.
Occasionally, numerical quantifiers are also used, with which it can be stated that a predicate applies to a certain number of individuals. However, these are not absolutely necessary because they can be traced back to the universal and existential quantifier as well as to the predicate of identity .
Predicates
The definition of a predicate given above as a sequence of words with clearly defined spaces, which becomes a statement if a proper name is inserted into each space, is a purely formal, meaningless definition. In terms of content, predicates can express very different conditions, for example terms (e.g. "_ is a person"), properties (e.g. "_ is pink") or relations , i. H. Relationships between individuals (e.g. "_ 1 is greater than _ 2 " or "_ 1 is between _ 2 and _ 3 "). Since the exact nature and the ontological status of terms, properties and relations are controversial or are viewed differently from different philosophical directions and since the exact delimitation of terms, properties and relations from one another is viewed differently, this formal definition is the most practical in terms of application. because it allows predicate logic to be used without having to accept certain ontological or metaphysical assumptions.
The number of different spaces in a predicate is called its arity. For example, a predicate with one space has one digit, one with two spaces has two digits, and so on. Occasionally, statements are used as zero-digit predicates, i.e. H. considered as predicates without spaces. When counting the spaces, only different spaces are taken into account.
In formal predicate logic, predicates are expressed using predicate letters, mostly uppercase letters from the beginning of the Latin alphabet, for example F_ 1 _ 2 for a two-digit predicate, G_ 1 for a one-digit predicate or H_ 1 _ 2 _ 3 for a three-digit predicate. The arguments of a predicate are often put in brackets and separated by commas, so that the examples mentioned would be written as F (_ 1 , _ 2 ) or G (_ 1 ) and H (_ 1 , _ 2 , _ 3 ).
Proper names and individual constants
In the philosophy of language and linguistics , the subject of proper names is quite a complex one. For the treatment in the context of an introductory representation of the predicate logic, it should be sufficient to designate such language expressions as proper names that designate exactly one individual; the word "individual" is understood here in a very general sense and means every "thing" (physical object, number, person ...) that can be distinguished from other things in any imaginable way. Proper names in the sense mentioned will usually be actual proper names (e.g. "Gottlob Frege") or markings (e.g. "the current Federal Chancellor of Austria").
The counterpart to the proper names of natural language are the individual constants of predicate logic; usually you choose lower case letters from the beginning of the Latin alphabet, for example a, b, c. In contrast to natural language proper names, each individual constant actually designates exactly one individual. This does not mean any implicit metaphysical prerequisites, but merely stipulates that only natural-language proper names with individual constants are expressed that actually designate exactly one individual.
With the vocabulary of predicate letters and individual constants, propositionally atomic sentences such as "Socrates is a person" or "Gottlob Frege is the author of the conceptual writing" can already be analyzed in their internal structure: If one translates the proper name "Socrates" with the individual constant a, the proper name " Thank God Frege ”with the individual constant b, the proper name or book title“ Concepts script ”with the individual constant c and the predicates“ _ is a person ”and“ _ 1 is the author of _ 2 ”with the predicate letters F_ and G_ 1 _ 2 , then “Socrates is a person” can be expressed as Fa and “Thank God Frege is the author of the 'conceptual writing'” as Gbc.
Quantifiers
With quantifiers, statements can be made about whether a sentence function applies to none, some or all of the individuals in the discourse universe. In the simplest case, the sentence function is a one-digit predicate. If one inserts an individual variable into the predicate and puts the existential quantifier and the same variable in front of it, then it is asserted that there is at least one individual to whom the predicate applies. So there must be at least one sentence of the form that an individual constant is inserted into the predicate, which is true in the relevant universe of discourse. The universal quantifier states that a predicate applies to all individuals from the discourse universe. In classical predicate logic, therefore, all atomic, all-quantified statements are true when the discourse universe is empty.
The existential quantifier is expressed in semi-formal language as “there is at least one thing so that ...” or “there is at least one (variable name) for which ...” applies. In formal language, the characters or are used. The universal quantifier is expressed in semi-formal language as "For all (variable name): ...", in formal language by one of the characters or .
Immediately apparent is the use of quantifiers for predicates, such as "_ is a human being." The existentially quantified statement loud would "There is at least one thing is true for that: it is a human being," in formal language: . M_ is the translation of the single-digit predicate "_ is a person" and is the existential quantifier. The letter x is not an individual constant, but fulfills the same function that the word “es” fulfills in the semi-formal formulation: Both mark the space to which the quantifier refers. In the example chosen, this appears to be redundant because it contains only one quantifier and only one space and therefore no ambiguity is possible. In the general case in which a predicate can contain more than one space and a sentence can contain more than one quantifier and more than one predicate, no unambiguous reading would be given without the use of suitable “cross-reference characters”.
The most common use of lowercase letters from the end of the Latin alphabet, such as the letters x, y, and z, is used to establish the relationship between a quantifier and the space it refers to; they are called individual variables. The space to which a quantifier refers or the variable that is used to establish this connection is referred to as being bound by the quantifier .
If you bind a space in a multi-digit predicate with a quantifier, then a predicate with one lower arity results. The two-digit predicate L_ 1 _ 2 , "_ 1 loves _ 2 ", which expresses the relation of loving, becomes a one-digit predicate by connecting the first blank with the universal quantifier , so to speak the property of being loved by everyone (the universal quantifier refers on the first blank where the individual stands from whom the love proceeds). By binding the second space, on the other hand, it becomes the one-digit predicate , the quality, so to speak, of loving everything and everyone (the universal quantifier binds the second space, i.e. the one in which the individual who plays the role of the beloved stands).
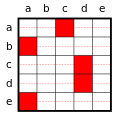
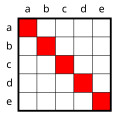
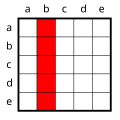
Sentences with predicates in which more than one space is bound by a quantifier are interesting. The possibility of handling such sentences is what makes predicate logic so powerful, but at the same time it is the point at which the system becomes a bit complicated for the newcomer and requires more intensive discussion and practice. As a small insight into the possibilities of predicate logic , all possibilities for binding the blanks with quantifiers should be listed for the simple two-digit predicate L_ 1 _ 2 , which can be read as "_ 1 loves _ 2 ", for example :
|
|
|
|||||||||||||
|
|||||||||||||||
The matrices illustrate the formulas for the case that five individuals come into question as lovers and lovers. Apart from sentences 6 and 9/10, these are examples. The matrix for sentence 5 is e.g. B. for "b loves himself"; the one for sentence 7/8 for “c loves b”.
It is important and instructive to distinguish between sentences 1,, and 3 ,,: In both cases everyone is loved; in the first case, however, everyone is loved by someone, in the second, everyone is loved by the same individual.
There are inferential connections between some of these sentences - for example, sentence 1 follows from sentence 3, but not the other way around (see Hasse diagram).
With three-digit predicates, formulas such as can be formed. With the predicate "x wants yz to love", this formula means "someone wishes everyone to love someone".
In natural language, quantifiers appear in very different formulations. Often words like “all”, “none”, “some” or “some” are used, sometimes the quantification is only recognizable from the context - for example, the sentence “people are mortal” usually means the universal statement that all people are mortal.
Examples (predicate logic - German)
| Predicate Logic - German | Explanation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
"All cats are mammals" (There can also be mammals that are not cats, |
|
||||||||||||
|
"Everything is a cat and a mammal" |
|
||||||||||||
|
"There is at least one city north of Munich" |
|
||||||||||||
|
"No city is north of itself" |
|
||||||||||||
|
"There is at least one daughter of Tom and Jenny" |
|
||||||||||||
|
"Every cat is a cat" |
|
||||||||||||
|
"Not all cars are green" (Either there are non-green cars or no cars at all in the discourse universe ) |
|
Some predicate logic equivalences
The logical equivalence between two predicate logical statements results from the schematic exchange of universal quantifier and existential quantifier. Some of the more frequently used predicate logic equivalences are exemplified below.
| The negation of the statement “Everything is green” can be formulated either as “Not everything is green” or as “There is something that is not green”. | |
| If the statement “There is something that is green” is denied, then “There is not one thing in the discourse universe that is green” or “Everything in the discourse universe is not green” is true and vice versa. | |
| Distributivity of the existential quantifier over OR. | |
| Distributivity of the universal quantifier over AND. | |
| If there is an example that implies a sentence, every example would imply that sentence. | |
| If a sentence implies a general statement, then the implication applies to every single example. |
If it is excluded that the discourse universe is empty, the following also apply:
Types of predicate logic
If - as outlined so far - quantifiers bind the blanks of predicates, then one speaks of predicate logic of the first order or order, English: first order logic , abbreviated FOL ; it is, so to speak, the standard system of predicate logic.
An obvious variation of the predicate logic consists in not only binding the blanks of predicates, i.e. not only quantifying them about individuals, but also making existence and universal statements about predicates . In this way one can formalize statements like “There is a predicate for which applies: it applies to Socrates” and “For every predicate: it applies to Socrates or it does not apply to Socrates”. In addition to the individual blanks of the first-level predicates, one would have introduced predicate blanks that lead to second-level predicates , for example “_ applies to Socrates”. From here it is only a small step to third-level predicates, in whose spaces second-level predicates can be inserted, and generally to higher-level predicates. One speaks in this case, therefore, of Logic higher level , English higher order logic , abbreviated HOL .
The formally simplest extension of the first-order predicate logic, however, consists in the addition of means for the treatment of identity . The resulting system is called first level predicate logic with identity . Identity can be defined in the predicate logic of a higher level, i. H. treat without language expansion, but one strives to work as long as possible and as much as possible on the first level, because there are simpler and, above all, complete calculations for this , i.e. H. Calculi in which all formulas and arguments valid in this system can be derived. This no longer applies to the higher-level predicate logic; H. it is not possible for the higher level to derive all valid arguments with a single calculus.
Conversely, one can restrict predicate logic of the first level, for example by restricting oneself to single-digit predicates. The logical system resulting from this restriction, the monadic predicate logic , has the advantage of being decidable ; This means that there are mechanical methods (algorithms) that can determine for every formula or for every argument of the monadic predicate logic in a finite time whether it or whether it is valid or not. For some purposes, monadic predicate logic is sufficient; In addition, the entire traditional conceptual logic , namely the syllogistics , can be expressed in monadic predicate logic.
Parallel to the already thematized differentiation of predicate logic systems according to their level or order, there are classic and non- classic forms. From classical predicate logic or generally of classical logic is called if and only if the following two conditions are met:
- the treated system is bivalent, i.e. H. each statement assumes exactly one of exactly two truth values, mostly true and false ( principle of two- valued ); and
- the truth value of statements that are composed by propositional logic joiners is uniquely determined by the truth values of the composed statements ( extensionality principle ).
If one deviates from at least one of these principles, then non-classical predicate logic results . Of course, it is also possible within the non-classical predicate logic to limit oneself to single-digit predicates (non-classical monadic predicate logic), to quantify via individuals (non-classical predicate logic of the first level), to expand the system with identity (non-classical predicate logic of the first level with identity) or to extend the quantification to predicates (non-classical predicate logic of a higher level). A frequently used non-classical predicate logic system is the modal predicate logic (see modal logic ).
Semantics of predicate logic
Formal semantics can be established for each predicate logic system . For this purpose, an interpretation function is defined, a function in the mathematical sense that assigns a scope to the predicates of the formal predicate logic language and a truth value to the atomic sentences. First of all, a universe of discourse is established, that is, the totality of the distinguishable objects ("individuals") to which the predicate logic statements to be interpreted should relate. For the classic predicate logic, the individual language elements are then interpreted as follows:
- Individual constants
- Each individual constant is assigned exactly one element from the discourse universe, that is, each individual constant names exactly one individual.
- Single-digit predicates
- A set of individuals from the discourse universe is assigned to each single-digit predicate. In this way it is determined which individuals the predicate concerned applies to. For example, if the set is assigned to the single-digit predicate , then it is determined that to , to and to apply.
- Multi-digit predicates
- A set of - tuples from individuals from the discourse universe is assigned to each -digit predicate .
- statement
- In order to be able to determine the truth value of statements, the evaluation function must map the set of all well-formed statements into the set of truth values, i.e. for each statement in the language of predicate logic it must determine whether it is true or false. This is usually done recursively according to the following pattern (the evaluation function is denoted here with B ):
- B ( ) = true ( is a predicate logic statement here), if B ( ) = false; otherwise B ( ) = false. In other words, the negative of a false statement is true, the negative of a true statement is false.
- B ( ) = true ( are predicate logic statements here), if B ( ) = B ( ) = true; otherwise B ( ) = false. In other words: A conjunction is true if and only if both conjuncts are true; otherwise it is wrong.
- Analogous definitions are for all other logical operators prepared.
- B ( ), where is a one-digit predicate letter and is an individual constant, returns the truth value “true” if the interpretation of is an element of the interpretation of , in other words: if the individual named by falls under the predicate . Otherwise, B ( ) returns the truth value “false”.
- B ( ), where is a -digit predicate letter and up to are individual constants, returns the truth value "true" if the -tuple is an element of the interpretation of the predicate letter . Otherwise, B ( ) returns the truth value “false”.
- B ( ), where is an individual variable and is a one-digit predicate, in whose (one or more occurring) space is entered, delivers the truth value "true" if B ( ) delivers the truth value "true" - regardless of the individual for which stands. There is an individual constant that does not appear in and is the expression that arises if the individual variable is replaced by the individual constant in every occurrence . Otherwise, B ( ) = false. In other words: B ( ) is true if and only applies to all individuals of the discourse universe.
- B ( ), where is an individual variable and is a one-digit predicate, in whose (one or more occurring) space is entered, delivers the truth value “true” if, if at least one individual from the discourse universe applies, i.e. if it it is possible to assign an individual from the discourse universe to an individual constant that does not occur in such that B ( ) delivers the truth value “true”.
Alternatives
Before propositional logic and predicate logic flourished, conceptual logic dominated in the form of the syllogistics developed by Aristotle and relatively moderate extensions based on it. Two systems developed in the 1960s in the tradition of conceptual logic are described by their representatives as being equal to predicate logic (Freytag) or even superior (Sommers), but have found little response from experts.
The laws of predicate logic only apply if the domain of the examined individuals is not empty, i.e. H. if there is at least one individual (of whatever kind) at all. A modification of predicate logic that is not subject to this condition of existence is free logic .
application
Predicate logics are central to various foundations of mathematics .
There are also some specific applications in computer science : It plays a role in the design and programming of expert systems and in artificial intelligence . Logical programming languages are based in part on - often restricted - forms of predicate logic. One form of knowledge representation can be done with a collection of expressions in predicate logic.
The relational calculus , one of the theoretical foundations of database query languages such as SQL , also of predicate logic uses as a means of expression.
In linguistics , especially in formal semantics , forms of predicate logic are used to represent meaning .
Special types, extensions and systems
Types and extensions
Types and extensions of the predicate logic are described in the following detailed individual articles:
- Classical predicate logic and its extensions
- Nonclassical extensions of predicate logic
- Modal logic (modal predicate logic)
- Temporal logic
- Action logic
- Fixed point logic
Calculi for systems of predicate logic
Calculi for predicate logic systems are given in the following individual articles:
- Hilbert calculus (axiomatic calculus)
- Systems of natural reasoning , for example the Fitch calculus , sequential calculus
- Tree calculi
- Resolution (logic)
- Existential graphs
- Dialogic logic
literature
Introductions
- Jon Barwise, John Etchemendy: Language, Proof, and Logic. Volume 1: Propositional and Predicate Logic. Mentis, Paderborn 2005, ISBN 3-89785-440-6 .
- Jon Barwise, John Etchemendy: Language, Proof, and Logic. Volume 2: Applications and Metatheory. Mentis, Paderborn 2006, ISBN 3-89785-441-4 .
- Benson Mates : Elementary Logic - First Level Predicate Logic. Vandenhoeck & Ruprecht, Göttingen 1997, ISBN 3-525-40541-3 .
- Wesley C. Salmon: Logic. Reclam (= Universal Library), Stuttgart 1983, ISBN 3-15-007996-9 .
About history
- Karel Berka , Lothar Kreiser: Logic texts. Annotated selection on the history of modern logic. 4th edition. Akademie-Verlag, Berlin 1986.
- William Kneale , Martha Kneale : The Development of Logic. Clarendon Press, 1962, ISBN 0-19-824773-7 . Standard work on the history of logic (English)
Web links
- Uschi Robers: Formal representation of predicate logic . Technical university Dortmund.
- Klaus Dethloff, Christian Gottschall: Introduction to predicate logic . University of Vienna.
- Video: Predicate Logic . Pedagogical University Heidelberg (PHHD) 2012, made available by the Technical Information Library (TIB), doi : 10.5446 / 19823 .
Individual evidence
- ↑ Eric M. Hammer: Semantics for Existential Graphs . In: Journal of Philosophical Logic , Volume 27, Issue 5 (October 1998), p. 489: "Development of first-order logic independently of Frege, anticipating prenex and Skolem normal forms"
- ↑ There are extensions of the classical predicate logic that provide definition gaps for sentence functions, or additional truth values, for example to do justice to vague terms of natural language
- ↑ List of all formulas with three-digit predicates on Wikiversity .
- ↑ p. 4 in http://www2.informatik.uni-hamburg.de/wsv/teaching/vorlesungen/FGI1SoSe14/PL-Syntax-Semantik.pdf
- ↑ p. 4 in http://www2.informatik.uni-hamburg.de/wsv/teaching/vorlesungen/FGI1SoSe14/PL-Syntax-Semantik.pdf
- ↑ free logic in the English language Wikipedia