Existential graphs

Existential Graphs (the German translations "existential graphs" and "existence graphs" are not very common) are a logical system of the American logician and philosopher Charles Sanders Peirce . They include both their own graphic notation for logical statements and a logical calculus , i.e. H. (essentially) a formal system of inference rules with which existing statements can be transformed in such a way that new statements arise from the former.

introduction

Peirce found the algebraic notation (i.e. formula notation) of logic, especially that of the predicate logic, which was very new in his lifetime and which he himself helped to develop, as philosophically unsatisfactory, because the symbolic symbols were given their meaning through mere convention. In contrast, he aspired to a notation in which the characters take their meaning literally in itself - in the terminology of his theory of signs : a system of iconic characters that are similar to the objects and relations referred to or the same.

The development of an iconic, graphic and - as he intended - thus intuitive and easily learnable logical system was a project that kept Peirce busy all his life. After at least one discontinued approach - the "Entitative Graphs" - the closed system of Existential Graphs was finally created from 1896 on. Though considered by their creator to be a clearly superior and more intuitive system, they were, as a notation and as a calculus, of little influence on the history of logic; This is attributed, on the one hand, to the fact that Peirce published only little on this topic and the published texts were not written very clearly; and on the other hand on the fact that the linear formula notation in the hands of experts is the less laboriously manageable tool. The existential graphs received little attention or were seen as unwieldy notation.

From 1963, the work of Don D. Roberts and J. Jay Zeman, in which Peirce's graphic systems were systematically examined and represented, led to a better understanding. Today, however, only a modern application plays a practical role, the concept graphs introduced by John F. Sowa in 1976 , which are used in computer science to represent knowledge . As a research topic, the existential graphs are increasingly appearing again in connection with a growing interest in graphic logic, which is also expressed in attempts to replace the inference rules given by Peirce with more intuitive ones.

The overall system of existential graphs is made up of three subsystems that build on one another, the alphagraphs, the betagraphs and the gammagraphs. The alphagraphs are a purely propositional system . Building on them, the paragraphs emerge as a real extension, a first-level predicate logic system. The gammagraphs, which have not been fully researched to date and not completed by Peirce, are understood as a further development of the alpha and beta paragraphs. If interpreted appropriately, the gammagraphs cover higher-level predicate logic and modal logic . In 1903 Peirce began with a new approach, the "Tinctured Existential Graphs," with which he wanted to replace the previous systems of alpha, beta and gammagraphs and combine their expressiveness and performance in a single new system. Like the gammagraphs, the tinctured existential graphs remained unfinished.

As calculi, the alpha and beta paragraphs are both correct (i.e. all expressions that can be derived as alpha or beta paragraphs are semantically valid in terms of propositional or predicate logic ) and complete (i.e. all expressions that are semantically valid in propositional or predicate logic are alpha- or paragraphs can be derived).

Peirce justified the choice of the term "Existential Graphs" with the fact that the simplest meaningful and well-formed paragraph makes an existence statement. Peirce first used this term in late 1897; beforehand he speaks of “positive logical graphs” or simply of his system of logical diagrams.

This article treats the alpha and beta paragraphs as the most accomplished and best-researched part of Peirce's system. Additional information is provided by the works named in the literature list.

Alphagraphs

Notation of alphagraphs

Alphagraphs

Atomic statements , i.e. H. Statements that are not composed of other statements are - as usual in propositional logic - expressed by letters; for example, the atomic statement “It's raining” can be expressed by the letter “P”. The conjunction of several statements - atomic or non-atomic - is expressed by writing them next to one another. Therefore, to say that two statements P and Q are true, one writes “PQ”.

In addition to the conjunction, the system includes the negation . It is expressed in that the expression to be negated - regardless of whether it is simple or compound - is surrounded by a closed line, so to speak "ringed". There are no special requirements for the shape of the line, but it is common to use a circle or an oval. Peirce calls the closed line that denies a statement the cut (literally: cut). The pictorial background of the cut is that the statements assumed to be true are written down on the sheet of paper that is written on - the sheet of assertion . False statements have to be excluded, delimited, “cut off” from the area of true statements, and this is exactly the function of the cut.

To express a conditional , i. That is, to say that a statement P is a sufficient condition for a statement Q, a notation is chosen that is called “P scrolls Q”, “P curls Q”: The statement Q, that is the conditional sentence, stands within its own cut together with its condition, the statement P, in a second, outer cut (see figure, points c1 and c2). This notation is introduced atomically in the logical system of existential graphs, but in the knowledge that the cut is the negation and the juxtaposition is the conjunction, it can easily be brought into congruence with the truth conditions of these two connections: The conditional, P → Q, is equivalent to the negation ¬ (P ∧ ¬Q), and that is exactly the statement of the “P scrolls Q”, which precisely separates the case of the true P and false Q from the sheet of assertion , “cuts out”.

The disjunction is expressed by writing the two disjuncts - each placed separately in individual cuts - next to each other and adding an additional outer cut. One can easily see that this notation represents the statement ¬ (¬P∧¬Q) in modern notation, a statement that is equivalent to P∨Q. The pictorial background is again that the disjunction excludes the case from the sheet of assertion that both P and Q are false.

With the two links of the alphabets, the negation (the cut) and the AND link (writing down several statements on the acceptance sheet) - as was shown by way of example for the conditional and the disjunction - all other links of the two-valued propositional logic can be represented (see functional Completeness of joiners ). Alphagraphs are thus a fully-fledged notation for propositional logic.

If statements in the spelling of alphagraphs are to be processed by electronic computers or simply reproduced with word processing systems or earlier typewriters, one often makes do with expressing the cuts using brackets. Instead of drawing a closed line around the sentence P, write (P) in this case. The conditional, “P scrolls Q”, becomes (P (Q)) in this notation. This article is used for typographical reasons.

Final rules of the alphagraphs

In order to be able to formulate the rules, it is first necessary to define the concept of the level of a statement (in literature: “proposition level”). The level of a - elementary or compound - statement is defined as the number of cuts that directly or indirectly surround this statement. For example, in the expression (P (Q)), the plane of P and that of (Q) are 1 because both P and (Q) are only part of the outer cut. The level of Q, on the other hand, is 2, because Q is not only immediately surrounded by a cut, but this in turn is part of the outer cut.

After this preliminary remark, the final rules can be stated as follows:

adoption: The rule of assumption makes it possible to write down any statement as a premise and to draw conclusions from it. If you want to derive an argument that includes more than one premise, then you write the premises next to each other - writing next to each other means nothing other than accepting each of the combined sentences.
R1 - Rule of Erasure: Any statement that occurs on an even-numbered level may be deleted without replacement. With this rule one can, for example, infer from (P (Q)) by deleting Q to (P ()), because Q is on level 2 and 2 is an even number. In this example, P should not be deleted because P is on level 1 and 1 is an odd number.
R2 - Rule of Insertion: Any statement may be inserted at the odd-numbered level. For example, it is permissible to infer (PR (Q)) from (P (Q)) with this rule: The inserted statement, R, comes on level 1 and 1 is an odd number.
R3 - Rule of Iteration: Any statement that is part of a compound statement may be repeated on the same level or on a lower level, but not within itself. According to R3, for example, from (P (Q)) by repeating P on the same level on (P ( Q) P) or by repeating P at a lower level to (P (QP)). Likewise, the same statement can be used to infer (P (Q) (Q)) by repeating (Q). It would not be permissible to repeat (Q) within oneself and thus to infer (P (Q (Q))) - this theoretical possibility is excluded by the additional condition that the repetition of a statement must not be made within itself.
R4 - Cancellation of repetition ("Rule of Deiteration"): If a statement X is formally of a form that it could have arisen from a statement Y by applying R3, the repetition rule, then R4 can be used to infer from X to Y; it is not necessary that X actually came about through an application of R3. For example, R4 can be used to infer from (P (Q) (Q)) to (P (Q)), because R3 can be used to infer from (P (Q)) to (P (Q) (Q)).
R5 - Rule of the Double Cut: Double cuts can be inserted and deleted as desired, both around existing statements and on their own. For example, according to R5, one may infer from PQ to P ((Q)), to ((P)) Q and also to ((PQ)). However, it is also possible to infer from PQ to PQ (()) or to P (()) Q.

example

It should be derived from and the statement ( chain link ). To do this, one begins with the assumptions (P (Q)) and (Q (R)) and gradually derives the statement (P (R)): ${\ displaystyle P \ rightarrow Q}$ ${\ displaystyle Q \ rightarrow R}$ ${\ displaystyle P \ rightarrow R}$

(P (Q)) (Q (R))	${\ displaystyle \ longrightarrow}$	(P (Q (Q (R)) )) (Q (R))	(R3)
(P (Q (Q (R)))) (Q (R))	${\ displaystyle \ longrightarrow}$	(P (Q (Q (R))))	(R1)
(P ( Q ( Q (R))))	${\ displaystyle \ longrightarrow}$	(P (Q ((R))))	(R4)
(P (Q (( R )) ))	${\ displaystyle \ longrightarrow}$	(P (QR))	(R5)
(P ( Q R))	${\ displaystyle \ longrightarrow}$	(P (R))	(R1)

Paragraphs

The paragraphs are the predicate logic system of the existential graphs. They expand the system of alphagraphs by the linguistic element of the line of identity and generalize the already existing rules of closure.

The atomic expressions in the paragraphs are no longer statement letters (P, Q, R, ...) or statements ("It's raining," "Peirce died in poverty"), but predicates in the sense of predicate logic (see there for details), possibly abbreviated to predicate letters (F, G, H, ...). A predicate in the sense of predicate logic is a sequence of words with clearly defined spaces that becomes a statement if a proper name is inserted into each space. For example, the sequence of words “_ died in poverty” is a predicate because the sentence “Peirce died in poverty” arises from it if the proper name “Peirce” is entered in the space. Likewise, the word sequence "_ ₁ is richer than _ ₂ " is a predicate, because the statement "Socrates is richer than Plato" arises from it if the proper names "Socrates" or "Plato" are used in the spaces.

Notation of the paragraphs

The basic linguistic element is the “line of identity”, a thick line of any shape. The identity line docks onto the blank space of a predicate to show that the predicate applies to at least one individual. In order to express that the predicate "_ is a person" applies to at least one individual - to say that there is (at least) one person - one writes an identity line in the space of the predicate "_ is a person:"

There is at least one person.
Predicate logic: ∃xMensch (x)

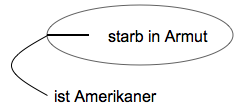
If an identity line connects two or more blanks - regardless of whether they are different predicates or the same predicate - then it expresses that there is at least one individual who - written in the respective space - makes each of these predicates true at the same time. A simple example is the following paragraph. In this graph, the identity line expresses that there is at least one object that fulfills both the predicate “_ is American” and the predicate “_ died in poverty” - in other words, that there is at least one American who lives in Poverty died.

At least one American died in poverty.
Predicate logic: ∃x (Americans (x) ∧Dying in poverty (x))

The following must be clearly distinguished from this paragraph, which is composed according to the rules of the alphagraphs:

There is at least one American. At least one individual died in poverty.
Predicate logic: ∃xAmericans (x) ∧ ∃yDying-in-Poverty (y)

In this case there are two separate paragraphs written one below the other. The upper subgraph indicates that at least one individual fulfills the predicate "_ is American", i. that is, there are Americans. The lower subgraph states in an analogous way that at least one individual fulfills the predicate “_ died in poverty”, i. that is, at least one individual died in poverty. To write two paragraphs side by side or one below the other means, according to the rules of the alphabets, to state the truth of both. The combined graph says that there is at least one American and that at least one individual died in poverty - but it does not claim that individuals who have one predicate also have the other.

Through a suitable combination of the identity line with the known propositional means of the alphagraphs, almost all predicate logic statements can be formulated.

A simple case is the negation of an existence statement. In the following example the statement of the first example, i. That is, the statement that there are people is negated by being written within a cut. So it is stated that it is not the case that there are people - in more beautiful German: that there are no people.

There are no human
predicate logic: ¬∃xHuman (x)

The following one differs from this graph, in which the identity line appears to protrude from the cut:

There is at least one individual who is not human.
Predicate logic: ∃x¬Human (x)

According to the reading of the paragraphs, there is a connection between two graphs: an outer, empty identity line that simply says: “Something exists;” and an identity line within the cut that says for itself: It is not the case that there is at least one An individual who fulfills the predicate "_ is a person". The connection of the two lines at the point where they cut the cut expresses the identity of the representational individuals: “There is something, and this something is not human.” The above paragraph expresses nothing other than the statement that there are things are not human.

An identity line located within a cut can just as easily be connected to an outer identity line, which in turn docks to a predicate. The graph below is an example of this constellation. Taken by itself, the cut says: It is not the case that there is an individual who died in poverty; and taken on its own, the outward expression states that there is at least one individual who is American. Since both expressions of identity lines touch each other in the cut, the overall expression expresses the identity of both individuals, so it says: There is at least one American who did not die in poverty.

There is at least one American who did not die in poverty
Predicate logic: ∃x (Americans (x) ∧¬Dying in poverty (x))

A general statement of the type “All pigs are pink” would be represented by a paragraph of the following type. Literally this is the negation of a sentence of the type in the previous example, specifically the negation of "There is at least one pig that is not pink." To deny that there are non-pink pigs, however, now means to say that all pigs are actually pink.

All pigs are pink.
Predicate logic: ∀x (Pig (x) → Pink (x)) or literally ¬∃x (Pig (x) ∧¬Rosa (x))

If an identity line is marked with an empty cut, as in the following example, this expresses the non-identity of the individuals who fill the spaces at which the identity line docks. In this sense, the example opposite says that there is at least one pig and that there is at least one pink individual, but both of them are not identical.

There is at least one pig and there is at least one pink thing that is not the same.
Predicate logic: ∃x∃y (Pig (x) ∧Pink (y) ∧¬x = y)

Analogous to the preceding paragraph, the following paragraph expresses that there are at least two pigs: "There is a pig, and there is (another) pig that is not identical to the former."

There are at least two pigs.
Predicate logic: ∃x∃y (Pig (x) ∧Pig (y) ∧¬x = y)

Final rules of the paragraphs

In the system of paragraphs, no genuine predicate logic inference rules are added, but the existing rules are modified. In detail, the familiar final rules are given the following new wording:

R1 - Rule of Erasure: Any statement that is on an even-numbered level and any part of an identity line that occurs on an even-numbered level may be deleted without replacement.

An application of the deletion rule (R1)

R2 - Rule of Insertion: Any statement may be inserted on the odd-numbered level and two or more unconnected ends of identity lines may be connected with one another as desired.

An application of the insertion rule (R2)

R3 - Rule of Iteration

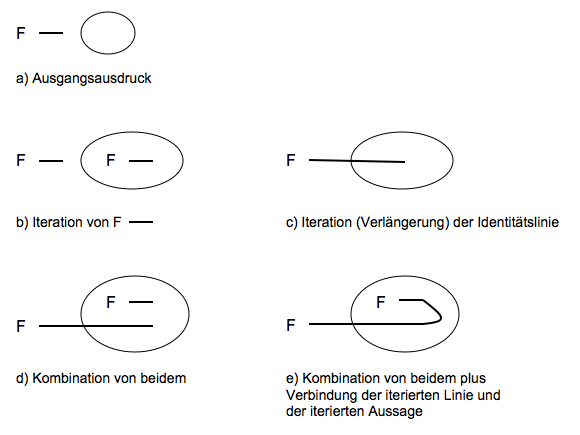
Any statement that is part of a compound statement may be repeated on the same level or below, but not within itself. The following iterations are permitted for identity lines:

An additional identity line with a loose end can be added to an existing identity line at any time, i. H. an identity line that does not dock on any space in a predicate or on any other identity line. The identity line attached in this way must not touch or cross a cut.
Each identity line with a loose end may be extended so that its new end comes to lie on the same or a lower level.
The iteration of a statement and the iteration of an identity line may be combined with one another in such a way that the loose end of the iterated identity line is connected to the iterated statement.

Applications of the repetition rule (R3)

R4 - Cancellation of repetition ("Rule of Deiteration"): If a statement X is formally of a form that it could have arisen from a statement Y by applying R3, the repetition rule, then R4 can be used to infer from X to Y; it is not necessary that X actually came about through an application of R3.

R5 - Rule of the Double Cut: Double cuts can be inserted and deleted as desired, both around existing statements and on their own. Duplicate cuts can also be inserted in such a way that they intersect identity lines, but both inserted cuts must always intersect all cut lines.

Further examples

swell

^ "Development of first-order logic independently of Frege, anticipating prenex and Skolem normal forms" (Hammer 1998, page 489)
↑ "Peirce wants a sign which will not merely be conventionally understood [...], but which will ″ wear its meaning on its sleeve, ″ so to speak" (Zeman 1964, page 21, quoted from the online edition)
↑ "[algebraic formulas] are not 'iconic' - that is, they do not resemble the objects or relationships they represent. Peirce took this to be a defect. "(Roberts 1973, p. 17)
↑ "[Peirce's] graphical publications were few and not easy to understand, as he admitted himself." (Roberts 1973, page 12)
^ "[T] the syntax of Peirce's graphs lacks, at least in general, the combinatorial elegance and simplicity of linear notations" (Hammer 1998, page 502)
↑ Roberts points out that even the standard work on the history of logic, Kneale / Kneale : The Development of Logic. Clarendon Press. Oxford 1962, ISBN 0-19-824773-7 , not mentioning Peirce's logical diagrams.
↑ “One questions the efficacy of Peirce's diagrams […]. Their basic machinery is too complex […]. "(Quine: Review of Collected Papers by Charles Sanders Peirce, Volume 4: The Simplest Mathematics, Isis 22, page 552, quoted from Roberts 1973, page 13)
^ "Aside from their historic interest, Peirce's graphical formalisms are of current interest. Sowa's system of conceptual graphs […] is based on Peirce's work. [Other work] also indicates increasing interest in the logic of graphical reasoning. "(Hammer 1998, page 489)
↑ see e.g. B. Sun-Joo Shin: "Reconstituting Beta Graphs into an Efficacious System", Journal of Logic, Language and Information archive, Volume 8, Issue 3, July 1999, pages 273-295
↑ The evidence for this was provided by J. Jay Zeman in his dissertation in 1964 (see list of references); for the alphagraphs see also the work by White, 1984
↑ More precisely, but not quite as understandable: with the fact that the "fundamental symbol" of the paragraphs expresses a "relation of existence" (quoted from Roberts, page 30)
^ Letter to William James, December 18, 1897, quoted from Roberts, p. 30
↑ The presentation of the rules of inference and their numbering follows the presentation in Don D. Roberts book The Existential Graphs of Charles S. Peirce , pp. 40-45.
↑ The presentation follows particularly closely Roberts, pp. 56–60

literature

Primary literature

Charles Hartshorne , Paul Weiss (eds.): The Collected Papers of CS Peirce , Cambridge: Harvard 1931-35 (reprint of Volume 3 and Volume 4: Harvard University Press 1987, ISBN 0-674-13801-5 ) - in particular pages 320 -470 and 530-572 of Volume IV. Available online:

Secondary literature

Monographs

Don D. Roberts: The Existential Graphs of Charles S. Peirce , The Hague: Mouton 1973 (= Approaches to Semiotics 27) - the standard introductory work to the Existential Graphs, in English
Sun-Joo Shin: The Iconic Logic of Peirce's Graphs, Cambridge, Massachusetts: MIT Press, Bradford 2002, ISBN 0-262-19470-8 - most recent monograph on the subject
J. Jay Zeman: The Graphical Logic of CS Peirce , Chicago: 1964 (dissertation), available online at [1] - groundbreaking, highly formal presentation in which, among other things, the completeness and correctness of alpha and beta paragraphs is shown

items

Eric M. Hammer: Semantics for Existential Graphs, Journal of Philosophical Logic , Volume 27, Issue 5 (October 1998), pages 489-503
Dennis Higgins, Bram Van Heuveln, Elizabeth Hatfield, Deborah Kilpatrick, Lut Wong: "A Java implementation for Peirce's existential graphs," Journal of Computing Sciences in Colleges , Volume 16 Issue 3, March 2001, online for a fee under [2] - dealt with a Java implementation, but introduces a compact introduction to alphagraphs
Richard B. White, "Peirce's Alpha Graphs: The Completeness of Propositional Logic and the Fast Simplification of Truth Functions," Transactions of the Charles S. Peirce Society , Volume 20, Number 4, 1984, pp. 351-361

Web links

Commons : Existential graphs - collection of images, videos and audio files

Eric Hammer: Peirce's Deductive Logic. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
Mary Keeler: The Philosophical Context of Peirce's Existential Graphs
Existential Graphs MS 514 by Charles Sanders Peirce with commentary by John F. Sowa (English)
Peirce Edition Project (English)
Peirce Proof Builder - a Java applet for interactive proofing in Peirce's system of alphagraphs
Existential Graphs - another Java applet for interactive proof in the system of alphagraphs
Homepage of Dr. Frithjof Dau with extensive material on the topic of Existential Graphs (including scans of Peirce's original notes on the Existential Graphs MS 145)

This article was added to the list of excellent articles on December 1, 2006 in this version .

[1] "Development of first-order logic independently of Frege, anticipating prenex and Skolem normal forms" (Hammer 1998, page 489)

[2] "Peirce wants a sign which will not merely be conventionally understood [...], but which will ″ wear its meaning on its sleeve, ″ so to speak" (Zeman 1964, page 21, quoted from the online edition)

[3] "[algebraic formulas] are not 'iconic' - that is, they do not resemble the objects or relationships they represent. Peirce took this to be a defect. "(Roberts 1973, p. 17)

[4] "[Peirce's] graphical publications were few and not easy to understand, as he admitted himself." (Roberts 1973, page 12)

[5] "[T] the syntax of Peirce's graphs lacks, at least in general, the combinatorial elegance and simplicity of linear notations" (Hammer 1998, page 502)

[6] Roberts points out that even the standard work on the history of logic, Kneale / Kneale : The Development of Logic. Clarendon Press. Oxford 1962, ISBN 0-19-824773-7 , not mentioning Peirce's logical diagrams.

[7] “One questions the efficacy of Peirce's diagrams […]. Their basic machinery is too complex […]. "(Quine: Review of Collected Papers by Charles Sanders Peirce, Volume 4: The Simplest Mathematics, Isis 22, page 552, quoted from Roberts 1973, page 13)

[8] "Aside from their historic interest, Peirce's graphical formalisms are of current interest. Sowa's system of conceptual graphs […] is based on Peirce's work. [Other work] also indicates increasing interest in the logic of graphical reasoning. "(Hammer 1998, page 489)

[9] see e.g. B. Sun-Joo Shin: "Reconstituting Beta Graphs into an Efficacious System", Journal of Logic, Language and Information archive, Volume 8, Issue 3, July 1999, pages 273-295

[10] The evidence for this was provided by J. Jay Zeman in his dissertation in 1964 (see list of references); for the alphagraphs see also the work by White, 1984

[11] More precisely, but not quite as understandable: with the fact that the "fundamental symbol" of the paragraphs expresses a "relation of existence" (quoted from Roberts, page 30)

[12] Letter to William James, December 18, 1897, quoted from Roberts, p. 30

[13] The presentation of the rules of inference and their numbering follows the presentation in Don D. Roberts book The Existential Graphs of Charles S. Peirce , pp. 40-45.

[14] The presentation follows particularly closely Roberts, pp. 56–60