Conceptual writing

The title page of the conceptual writing

The term writing is a narrow, only about eighty page comprehensive book by the Jena mathematician and philosopher Gottlob Frege on logic . It was published in 1879 with the subtitle "One of the arithmetic simulated formula language of pure thought" and is generally considered to be the most important publication in the field of logic since Aristotle 's Organon .

In this book, Frege succeeded for the first time in formalizing classical predicate logic and thus the first formalization of a logic in which a sufficiently large part of mathematics, but also of natural language, could be expressed. Together with George Boole's Mathematical Analysis of Logic from 1847, the conceptual writing therefore marks the beginning of modern formal logic. The term conceptual writing is also used for the logical calculus defined by Frege and for Frege's logical notation . Frege designed the term script to support his research on the fundamentals of mathematics.

Frege's calculus introduced the universal quantifier and multi-digit predicates (relations) for the first time . It is a classic second-level predicate logic calculus with identity , but in a two-dimensional notation that is idiosyncratic compared to today's spellings.

Position of the conceptual writing in the complete works of Freges

Despite its epoch-making importance, the term is not Frege's main work. It was followed in 1884 by The Fundamentals of Arithmetic and in 1893 and 1903 by the two volumes of the Basic Laws of Arithmetic , which, due to their size, can also be considered Frege's main work.

Frege around 1880, around the time the term writing was published

Frege's primary goal was to identify mathematics as part of logic, i.e. to show that all mathematical propositions can be derived from a few purely logical axioms (cf. logicism ). This company was only promising if a means was available by which the integrity of a key chain could be verified beyond doubt. Since the traditional Aristotelian logic ( syllogistics ) turned out to be useless for this purpose, Frege first took on the task of creating a new, more suitable logic. This was done in the form of conceptual writing . For Frege, the conceptual writing was therefore only the first stage on the way to a complete formalization of mathematics as a whole, which he carried out in part in the basic laws of arithmetic for number theory . Frege's logistic program initially failed (before the publication of the second volume of the Basic Laws ) because of Russell's antinomy , but it was continued by Bertrand Russell , Rudolf Carnap, and others.

However, the term was by no means intended exclusively for use in mathematics. On the contrary, Frege placed his writing in the foreword expressly in the context of Leibniz's idea of a lingua characterica universalis , a universal language that was supposed to represent an ordered system of all concepts based on a mathematical model. Frege's font, presented in 1879, was intended to form the logical heart of such a universal language. It can be assumed that the term conceptual writing is borrowed from a treatise by Friedrich Adolf Trendelenburg on Leibniz's draft of this universal language, which Frege quotes in the foreword. Incidentally, the word “concept writing ” was in common use around the turn of the 20th century as a Germanization of “ ideography ”.

notation

The introduction of logical symbols in conceptual writing .
Please click on the preview to open it.

Frege used in the Begriffsschrift a specially created by him notation (Notation) for expressions of the propositional and predicate logic . The notation of the conceptual writing is a graphic, two-dimensional representation in which formulas are connected with one another by horizontal and vertical lines. It uses signs for the negation and the conditional as the propositional logic element and the universal quantifier as the predicate logic element. Just like the Polish notation - albeit linear, one-dimensional and therefore much more space-saving - much later , the conceptual notation gets by without brackets.

syntax

The Begriffsschrift knows only two syntactic basic elements: functional expressions and proper names, both by variables can be represented. All syntactic operations follow the scheme function - argument - value: By applying a function with n free positions to n arguments, a certain value of the function is obtained.

More on the concept of a function: If, for example, in the complex expression '1 × 1', you replace both occurrences of the number sign '1' by the variables 'n' or 'm', you get the function expression 'n × m'. The variables make it clear that the term “unsaturated” is, as Frege says: in this form it does not designate an object, but needs to be completed by two arguments. Renewed substitution of numerals for the variables results in a series of arithmetic terms , e.g. B. '1 × 1', '1 × 2', '2 × 1' etc. The various possible substitutions for the variables are argument expressions. What is denoted by the complex expression is the value of the function. For example, the value of the function n × m for arguments 2 and 3 is the number 6.

This basic scheme is by no means limited in its applicability to the field of mathematics: If, for example, in 'The Conqueror of x' the variable 'x' is replaced by 'Gaul', the function takes on the value Julius Caesar. According to Frege, predicates are also functions: The function expressed by 'x conquered Gaul' takes the value true for the argument Julius Caesar and the value false for the argument Hannibal. The replacement of the subject-predicate-form by the function-argument-form of the judgment was already a considerable advance compared to traditional logic, because it made it possible to formulate a logic of relations: modern logic (unlike syllogistics) also knows it Two- and multi-digit predicates (relational expressions), such as 'x loves y', 'x stands between y and z' etc. (see also Logic - Classical Logic .)

Truth functionality

Frege now took all compound expressions as the results of applying a function to arguments; in particular, he also treated those expressions as functional expressions that are now commonly known as joiners . Their arguments are statements, the truth values true and false, which Frege calls "the true" and "the false". In order to indicate the meaning of a connective, it is sufficient to define the conditions under which a statement with this connective becomes true or false. Today this connection is called truth functionality, and the truth conditions are usually given in the form of so-called truth tables . The truth functionality is an essential prerequisite for the establishment of an extensional semantics as developed by Alfred Tarski in the 1930s.

Content line and judgment line

The horizontal "content line" states in the Begriffsschrift , that what follows it, a (to truth or falsity back) "beurtheilbarer content" is one in modern terminology statement that can be true or false. The content line does not determine whether a statement is true; it is not asserted, but only "put in the room" as potentially true or false:

Mind you would be an absurd connection appears as "- 2" in the Begriffsschrift non-syntax unconstitutional; their worth would be wrong. This has to do with the fact that Frege's conceptual writing is pure term logic; Statements are also singular terms, to a certain extent different names for the two truth values.

The vertical "judgment line" in front of the content line indicates that the content is true:

Frege said the content was expressed with "assertive force".

Junctures

Conceptual writing notation: propositional logic

Of the five common today, Frege used 'not', 'and', 'or', 'if - then', 'exactly if' only two: 'not' ( negation ) and 'if - then' ( implication or Conditional). The negation is shown by adding a small vertical line to the content line. The negation "not A" ( ) is expressed as follows: ${\ displaystyle \ lnot A}$

The value of this function is true if and only if the truth value of '- A' is not true, otherwise it is false.

The implication (read: 'if B, then A') is carried through in the conceptual writing ${\ displaystyle B \ rightarrow A}$

expressed. Frege wrote about the meaning of this combination of signs:

"If A and B mean evaluable contents, then there are the following four possibilities:

A is affirmed and B is affirmed;

A is affirmed and B is denied;

A is denied and B is affirmed;

A is denied and B is denied.

now means the judgment that the third of these possibilities does not take place, but one of the other three . "

In a formulation that seems unusual today, these are the truth conditions of the material implication : The implication is only false if the antecedent is true and the consequent is false.

Disjunction ('or') and conjunction ('and') can be expressed by combining these two joiners: the disjunction becomes through

- - Expressed the conjunction by ${\ displaystyle \ neg B \ rightarrow A}$

- . Since Frege's logic is a term logic in which statements are also singular terms, the “sign of content equality” (identity sign ) also serves as an expression of material equivalence . ${\ displaystyle \ neg (B \ rightarrow \ neg A)}$ ${\ displaystyle \ equiv}$

Quantifiers

Conceptual notation: predicate logic

As a universal quantifier, Frege uses an indentation (“cavity”) in the content line, into which the variable to be bound is written (see adjacent graphic). Due to the equivalence that applies in classical predicate logic

{\ displaystyle \ exists xF (x) \ leftrightarrow \ lnot \ forall x \ lnot F (x)}

a separate existential quantifier is not required; its content can be expressed by the universal quantifier and negator.

The following example shows the statement “for every x with the property F there is a y to which x is related to R” (e.g. “every person has a mother”). It illustrates the two main achievements of conceptual writing, which differentiate it from traditional syllogistics as well as from contemporary logical algebra : nested quantifiers ("for all x there is a y") and multi-digit predicates ("R (x, y)" ).

From this statement it follows with axiom 9 ( see below ):

From this, in connection with the statement "F (c)" with the help of the rule modus ponens ( see below ), the statement "there is a y to which c is in R" can be derived:

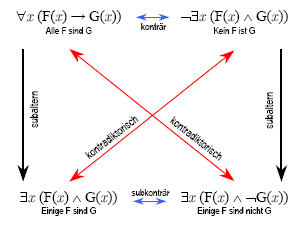
The quantifier logic allows (provided that the subject term is not empty) all the inferences of traditional logic. The figure below shows the " logical square " on the left from the original edition of the term script , on the right one in modern notation for comparison:

The logical square from the original edition of the conceptual writing

The fact that Frege says “contrary” instead of “subcontra” in the bottom line is obviously an oversight.

See also the tabular overview of the notation at the end of the article.

The axiom system of conceptual writing

After the explanations of the notation in the first chapter, Frege goes on in the second chapter with the heading “Presentation and deduction of some judgments of pure thought” to prove some logically true propositions on the basis of a few axioms.

Frege non-formally justified his nine axioms by explaining why they are true in their intended interpretation. Translated into modern notation, the axioms are:

${\ displaystyle \ vdash \ \ A \ to \ left (B \ to A \ right)}$
${\ displaystyle \ vdash \ \ (A \ to (B \ to C)) \ \ to \ \ left (\ left (A \ to B \ right) \ to \ left (A \ to C \ right) \ right) }$
${\ displaystyle \ vdash \ \ \ left (D \ to \ left (B \ to A \ right) \ right) \ \ to \ \ left (B \ to \ left (D \ to A \ right) \ right)}$
${\ displaystyle \ vdash \ \ \ left (B \ to A \ right) \ \ to \ \ left (\ lnot A \ to \ lnot B \ right)}$
${\ displaystyle \ vdash \ \ \ lnot \ lnot A \ to A}$
${\ displaystyle \ vdash \ \ A \ to \ lnot \ lnot A}$
${\ displaystyle \ vdash \ \ \ left (c \ equiv d \ right) \ to \ left (F (c) \ equiv F (d) \ right)}$
${\ displaystyle \ vdash \ \ c \ equiv c}$
${\ displaystyle \ vdash \ \ \ left (\ forall xF (x) \ right) \ \ to \ F (c)}$

In Frege's own numbering, these are sentences 1, 2, 8, 28, 31, 41, 52, 54 and 58. (1) - (3) relate to the material implication, (4) - (6) the negation. (7) and (8) concern identity: (7) is Leibniz's identity principle . (8) calls for the reflexivity of identity. (9) allows the transition from an all-quantified statement to any instance. All other propositions are derived from these axioms.

The conceptual writing has three rules of inference . Two of them, the modus ponens and the generalization rule, are mentioned explicitly. The ponens mode allows the transition from and to . The generalization rule allows the transition from to if the variable 'x' does not appear in P. The third rule, not explicitly mentioned, is a principle of substitution . ${\ displaystyle \ vdash A \ to B}$ ${\ displaystyle \ vdash A}$ ${\ displaystyle \ vdash B}$ ${\ displaystyle \ vdash P \ to A (x)}$ ${\ displaystyle \ vdash P \ to \ forall xA (x)}$

The fragment of the calculus given in the notation corresponding to a predicate logic of the first level is complete and free of contradictions . It was not until the system was expanded to include a theory of the scope of terms, which Frege later introduced in the fundamental laws of arithmetic , that led to inconsistency .

The third chapter is entitled “Some from a general series teaching”. The most important results concern the inheritance of a trait in a row and the succession in a row. If a relation R is given, then a property F according to Frege is hereditary in the R series if and only if:

{\ displaystyle \ forall x \ forall y \ (F (x) \ land xRy \ to F (y))}

Then Frege defines: b follows a in the R-series if and only if b has every hereditary property in the R-series that all x have with aRx. If you write R * for this relation of following in the R series, Frege's definition can be reproduced as follows:

{\ displaystyle aR ^ {\ ast} b \ equiv \ forall F [\ forall x (aRx \ to F (x)) \ wedge \ forall x \ forall y (F (x) \ wedge xRy \ to F (y) ) \ to F (b)]}

Shorter, where "Erbl (F, R)" should mean "F is hereditary in the R-series":

{\ displaystyle aR ^ {\ ast} b \ equiv \ forall F [\ forall x (aRx \ to F (x)) \ wedge Erbl (F, R) \ to F (b)]}

About this R * -relation, Frege proves a few theorems that show that it is an order relation . These considerations are obviously intended as preliminary work for the two subsequent works on the fundamentals of number theory. If one considers the relation y = x + 1 as xRy, then 0R * y (or 1R * y) is the property of y to be a natural number .

Reception and effect

The term writing found a remarkably cool reception at first. Not least because of its unusual and difficult-to-read symbolism, the general public initially seems to have taken little notice of it. The tenor of the contemporary reviews was mostly subdued to critical. Concerns about the extensive, difficult-to-use spelling were unanimously expressed. Above all, however, the critics accused Frege of ignoring the algebraic approach in symbolic logic ( Ernst Schröder , Giuseppe Peano , George Boole , Augustus De Morgan , Charles Sanders Peirce ). The criticism is justified: it is noticeable that Frege completely ignores the dominant stream of formal logic and does not relate his own work to that of other contemporary researchers. He made up for this omission in a few essays immediately following the term writing .

Among the few who recognized the meaning of the conceptual writing early on were the British philosopher and mathematician Bertrand Russell , the phenomenologist Edmund Husserl , Frege's student Rudolf Carnap and the Austro-British philosopher Ludwig Wittgenstein , who wrote in the foreword to his famous Tractatus logico-philosophicus (1921) wrote: "All I want to say is that I owe much of the stimulation to my thoughts to the great works of Frege and the works of my friend Mr. Bertrand Russell."

The logistic program, to which the conceptual writing was only the prelude, was continued in particular by Russell and Alfred North Whitehead in their monumental Principia Mathematica (1910ff.), Which for some time was considered the standard canonical work on logic. Russell and Whitehead already essentially used one of the logical notations commonly used today, the so-called Peano-Russell notation, which is based on the spelling of algebra .

From Frege's symbolism, the sign , the combination of its judgment and content line, survived (probably through the mediation of the Principia Mathematica ) , but mostly in a generalized meaning as a derivation relation . Furthermore, the negation sign that Arend Heyting introduced in 1930 (originally to distinguish the intuitionistic negator from the classic) can be viewed as a content line with a negative line added. ${\ displaystyle \ vdash}$ ${\ displaystyle \ neg}$

Even if Frege's idiosyncratic spelling was not a great success, almost every work in modern logic is at least indirectly based on the basic idea of the conceptual writing . Since the logic also auxiliary and basic discipline u. a. mathematics, linguistics and computer science, the indirect effects of Frege's work can hardly be overlooked. In philosophy, until the very recent past, recognized personalities repeatedly refer to ideas from the term script , including Michael Dummett and Robert Brandom .

Tabular overview of the notation

Modern notation	Colloquial rendering	designation
no direct equivalent; a similarity in: ${\ displaystyle \ emptyset \ vdash A}$ ${\ displaystyle \ vdash A}$	in Frege and Russell: A is a fact modern: A is provable	Similarity in modern notation: derivation
${\ displaystyle \ lnot A}$	A is not the case for non-A	negation
${\ displaystyle B \ to A}$	If B, then A	Implication, conditional, subjunction
${\ displaystyle A \ land B}$ ${\ displaystyle \ neg (B \ to \ neg A)}$	A and B	conjunction
${\ displaystyle A \ lor B}$ ${\ displaystyle \ neg B \ to A}$	a or B	Disjunction, adjunction
${\ displaystyle A \ leftrightarrow B}$ ${\ displaystyle A \, = \, B}$	A if and only if B A equals B.	Equivalence, bisubjunction; identity
${\ displaystyle \ forall xF (x)}$	Everything is F	Universal quantification, universal quantification
${\ displaystyle \ lnot \ exists xF (x)}$ ${\ displaystyle \ forall x \ lnot F (x)}$	Nothing is F There is no F
${\ displaystyle \ exists xF (x)}$ ${\ displaystyle \ lnot \ forall x \ lnot F (x)}$	There is an F At least one x is F	Existential quantification, particular quantification
${\ displaystyle \ forall x (G (x) \ to F (x))}$	All G are F
${\ displaystyle \ exists x (G (x) \ land F (x))}$ ${\ displaystyle \ lnot \ forall x (G (x) \ to \ lnot F (x))}$	Some G are F At least one G is F
${\ displaystyle \ lnot \ exists x (G (x) \ land F (x))}$ ${\ displaystyle \ forall x (G (x) \ to \ lnot F (x))}$	No G is F. All G are not F.
${\ displaystyle \ exists x (G (x) \ land \ lnot F (x))}$ ${\ displaystyle \ lnot \ forall x (G (x) \ to F (x))}$	Some G are not F Not all G are F

expenditure

Conceptual writing. One of the arithmetic simulated formula language of pure thinking. Halle 1879. [Original edition]
Conceptual writing and other articles, edited by Ignacio Angelelli, Hildesheim 1964 u.ö. ISBN 978-3-487-00623-9
[This reprint edition has some small, but sometimes disruptive printing errors; in particular, the judgment line is missing on p. 1. See the note by Angelelli / Bynum in the literature list.]

literature

Ignacio Angelelli, Terrell Ward Bynum: Note on Frege's conceptual writing . In: Notre Dame Journal of Formal Logic . 7, No. 4, 1966, pp. 369-370. ISSN 0029-4527 . doi : 10.1305 / ndjfl / 1093958759 . (Essentially a list of corrections to the reprint edition of Angelelli's conceptual writing.)
Franz Bolck (Ed.): Conceptual writing. Jena Frege Conference: 7. – 11. May 1979. Jena 1979.
George Boolos: Reading the Conceptual Writing . In: Min . XCIV, No. 375, 1985, pp. 331-344. ISSN 0026-4423 . doi : 10.1093 / mind / XCIV.375.331 . Reprinted in: ders .: Logic, Logic, and Logic , Cambridge (Mass.) 1998, 202-219. ISBN 978-0-674-53767-5 .
John P. Burgess: On a Consistent Subsystem of Frege's Basic Laws . In: Notre Dame Journal of Formal Logic . 39, No. 2, 1998, pp. 274-278. doi : 10.1305 / ndjfl / 1039293068 .
Gottlob Frege: Applications of the conceptual writing. Lecture given at the meeting of January 24, 1879 of the Jena Society for Medicine and Science. In: Jenaische Zeitschrift für Naturwissenschaft 13 / Supplement II (1879) (meeting reports of the Jenaische Gesellschaft für Medizin und Naturwissenschaft for the year 1879), 29–33. (Included in the reprint edition by I. Angelelli.)
––– About the scientific justification of a conceptual writing. In: Journal for Philosophy and Philosophical Criticism 81 (1882), 48–56. (Included in the reprint edition by I. Angelelli.)
––– About the purpose of the conceptual writing. In: Jenaische Zeitschrift für Naturwissenschaft 16 (1883) Supplement, 1–10. (Included in the reprint edition by I. Angelelli.)
––– Boolean logical formula language and my terminology. In: ders .: Nachgelassene Schriften , 53–59.
––– Boolean computational logic and conceptual writing. In: ders .: Nachgelassene Schriften , 9–52.
––– Function and concept. (Lecture given at the meeting on January 9, 1891 of the Jena Society for Medicine and Science. Tangible in this: Function, concept, meaning .)
––– Legacy writings , edited by Hans Hermes, Friedrich Kambartel and Friedrich Kaulbach, Hamburg 1969; expanded second edition 1983. ISBN 978-3-7873-0490-5 .
––– Function, term, meaning. Five logical studies , edited by G. Patzig, Göttingen 1994 u.ö. ISBN 978-3-525-33377-8 .
JJ Green, Marcus Rossberg, Philip A. Ebert: The Convenience of the Typesetter. Notation and Typography in Frege's "Fundamental Laws of Arithmetic" . In: The Bulletin of Symbolic Logic . 21, No. 1, May 2015, pp. 15-30. (Describes the conceptual notation of the basic laws .)
Otfried Höffe: Small history of philosophy , Munich 2008. ISBN 978-3-406-57385-9 .
Tapio Korte: Frege's conceptual writing as a lingua characteristica . In: Synthesis . 174, No. 2, 2010, pp. 283-294. doi : 10.1007 / s11229-008-9422-7 .
Franz von Kutschera : Thank God Frege. An introduction to his work , Berlin / New York 1989. ISBN 978-3-11-012129-2 .
Danielle Macbeth: Frege's Logic , Cambridge (Mass.) 2005. ISBN 978-0-674-01707-8 .
Richard L. Mendelsohn: The Philosophy of Gottlob Frege , Cambridge 2005. ISBN 978-0-521-83669-2 .
Terence Parsons: On the consistency of the first-order portion of Frege's logical system . In: Notre Dame Journal of Formal Logic . 28, No. 1, 1987, pp. 161-168. doi : 10.1305 / ndjfl / 1093636853 .
Ernst Schröder: Advertisement from Frege's term writing. In: Journal for Mathematics and Physics 25 (1881), 81–94.
Hans Sluga: Frege against the Booleans . In: Notre Dame Journal of Formal Logic . 28, No. 1, 1987, pp. 80-98. doi : 10.1305 / ndjfl / 1093636848 .
John Venn: A Review of Frege's Conceptual Writing . In: Mind 5 (1880), 297.
Risto Vilkko: The Reception of Frege's conceptual writing . In: Historia Mathematica . 25, No. 4, November 1998, pp. 412-422. ISSN 0315-0860 . doi : 10.1006 / hmat.1998.2213 . (Contains an overview of contemporary reception.)
Matthias Wille: Gottlob Frege: Conceptual writing, one of the arithmetic simulated formula language of pure thinking. Berlin, Springer Spectrum, 2018 (Classical Science Texts), ISBN 978-3-662-45011-6 .
Michael Wolff : Frege's criticism of the Kantian judgment table in his 'concept writing' from 1879. In: Michael Wolff: The completeness of the Kantian judgment table. With an essay on Frege's 'conceptual writing'. Klostermann, Frankfurt 1995. ISBN 3-465-02811-2 , pp. 243-312.
Michael Wolff : Frege and the traditional image of syllogistics. In: Rüdiger Bubner and Gunnar Hindrichs (eds.): From logic to language. Klett-Cotta, Stuttgart 2007, ISBN 978-3-608-94448-8 . Pp. 272-285.

Web links

Wiktionary: Conceptual writing - explanations of meanings, word origins, synonyms, translations

Edward N. Zalta: Frege's Theorem and Foundations for Arithmetic. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
The term script in digital form for download
An illustration of the logical system of conceptual writing by Stanley N. Burris (in English)
A short introduction to Gottlob Frege's conceptual writing by Sven-Ake Wegner (Bergische Universität Wuppertal)
An interactive program for converting propositional expressions into conceptual notation (and other notations) by Christian Gottschall

Individual evidence

↑ Höffe: Brief history of philosophy. P. 318.
^ Cf. Sluga: "Frege against the Booleans"
↑ See Volker Peckhaus: Logic, Mathesis universalis and general science , Berlin 1997. ISBN 978-3-05-003111-8
↑ Cf. Tapio Korte: "Frege's concept writing as a lingua characteristica".
↑ An extremely critical sketch of the considerations on such a universal language can be found in the article "Universal Language" in: Fritz Mauthner: Dictionary of Philosophy , second, increased edition, Leipzig 1923. (online)
↑ See the article “Characteristica universalis” in: Friedrich Kirchner / Carl Michaëlis: Dictionary of Basic Philosophical Concepts, 5th edition. Leipzig 1907, 116–117. (on-line)
^ Adolf Trendelenburg: "About Leibniz's draft of a general characteristic," in: Philosophical treatises of the Royal Academy of Sciences in Berlin from the year 1856, Berlin 1857, 36–69; Reprinted in: ders .: Historical Contributions to Philosophy, Vol. 3: Vermischte Abhandlungen , Berlin 1867, 48–62.
↑ ^a ^b Vilkko: "The reception of Frege's logical symbolism ".
↑ See e.g. B. the keyword "ideography" in Brockhaus' Kleinem Konversations-Lexikon , 5th edition 1911. (online)
↑ See also Frege: Function and Concept .
↑ ^a ^b Frege: Wortsschrift , p. 5.
↑ Frege: Terminalsschrift , p. 24.
↑ See the editor's footnote in the reprint edition, p. 24.
↑ A transcription of the other sentences in modern notation can be found in the appendix by Richard L. Mendelsohn: The Philosophy of Gottlob Frege .
↑ Frege: Terminalsschrift , p. 26.
↑ Frege knew this principle from the Leibniz paper Non inelegans specimen demonstrandi in abstractis published in 1840 and later quoted it in his Fundamentals of Arithmetic (1884) in §65: "Eadem sunt, quorum unam potest substiti alteri salva veritate."
↑ Frege: Wortsschrift , p. 21. Cf. Kutschera: Gottlob Frege , p. 33f.
↑ Kutschera: Gottlob Frege , p. 34.
^ Parsons: On the consistency of the first-order portion of Frege's logical system .
^ Burgess: On a Consistent Subsystem of Frege's Basic Laws .
↑ Cf. Kutschera: Gottlob Frege , chap. 6-8.
↑ A detailed discussion can be found in Richard G. Heck: "A Note on the Major Results of Conceptual Writing"
↑ Frege: Wortsschrift , pp. 61f., Sentence 76.
↑ Sluga: "Frege against the Booleans", p. 80.
↑ These essays are only published in the Nachlassen Schriften .
↑ Ludwig Wittgenstein: Tractatus logico-philosophicus , foreword. Quoted from the critical edition by Brian McGuinness and Joachim Schulte, Frankfurt am Main 1989. ISBN 978-3-518-28959-4 .
^ Stephen C. Kleene: Introduction to Metamathematics , Amsterdam a. a. 1952 and ö. ISBN 978-0-7204-2103-3
↑ Arend Heyting: "The formal rules of intuitionist logic," in: session reports of the Prussian Academy of Sciences, phys.-math. Class , 1930, pp. 42-65.

This version was added to the list of articles worth reading on September 9, 2007 .

[1] Höffe: Brief history of philosophy. P. 318.

[2] Cf. Sluga: "Frege against the Booleans"

[3] See Volker Peckhaus: Logic, Mathesis universalis and general science , Berlin 1997. ISBN 978-3-05-003111-8

[4] Cf. Tapio Korte: "Frege's concept writing as a lingua characteristica".

[5] An extremely critical sketch of the considerations on such a universal language can be found in the article "Universal Language" in: Fritz Mauthner: Dictionary of Philosophy , second, increased edition, Leipzig 1923. (online)

[6] See the article “Characteristica universalis” in: Friedrich Kirchner / Carl Michaëlis: Dictionary of Basic Philosophical Concepts, 5th edition. Leipzig 1907, 116–117. (on-line)

[7] Adolf Trendelenburg: "About Leibniz's draft of a general characteristic," in: Philosophical treatises of the Royal Academy of Sciences in Berlin from the year 1856, Berlin 1857, 36–69; Reprinted in: ders .: Historical Contributions to Philosophy, Vol. 3: Vermischte Abhandlungen , Berlin 1867, 48–62.

[Vilkko-8] Vilkko: "The reception of Frege's logical symbolism ".

[9] See e.g. B. the keyword "ideography" in Brockhaus' Kleinem Konversations-Lexikon , 5th edition 1911. (online)

[10] See also Frege: Function and Concept .

[beurtheilbar-11] Frege: Wortsschrift , p. 5.

[12] Frege: Terminalsschrift , p. 24.

[13] See the editor's footnote in the reprint edition, p. 24.

[14] A transcription of the other sentences in modern notation can be found in the appendix by Richard L. Mendelsohn: The Philosophy of Gottlob Frege .

[15] Frege: Terminalsschrift , p. 26.

[16] Frege knew this principle from the Leibniz paper Non inelegans specimen demonstrandi in abstractis published in 1840 and later quoted it in his Fundamentals of Arithmetic (1884) in §65: "Eadem sunt, quorum unam potest substiti alteri salva veritate."

[17] Frege: Wortsschrift , p. 21. Cf. Kutschera: Gottlob Frege , p. 33f.

[18] Kutschera: Gottlob Frege , p. 34.

[19] Parsons: On the consistency of the first-order portion of Frege's logical system .

[20] Burgess: On a Consistent Subsystem of Frege's Basic Laws .

[21] Cf. Kutschera: Gottlob Frege , chap. 6-8.

[22] A detailed discussion can be found in Richard G. Heck: "A Note on the Major Results of Conceptual Writing"

[23] Frege: Wortsschrift , pp. 61f., Sentence 76.

[24] Sluga: "Frege against the Booleans", p. 80.

[25] These essays are only published in the Nachlassen Schriften .

[26] Ludwig Wittgenstein: Tractatus logico-philosophicus , foreword. Quoted from the critical edition by Brian McGuinness and Joachim Schulte, Frankfurt am Main 1989. ISBN 978-3-518-28959-4 .

[27] Stephen C. Kleene: Introduction to Metamathematics , Amsterdam a. a. 1952 and ö. ISBN 978-0-7204-2103-3

[28] Arend Heyting: "The formal rules of intuitionist logic," in: session reports of the Prussian Academy of Sciences, phys.-math. Class , 1930, pp. 42-65.

	This article is available as an audio file:
	Save \| Information \| 14:39 min (8.44 MB) Text of the spoken version
	More information on spoken Wikipedia