decagon

In the geometry of which is decagon or decagon any polygon having ten sides and ten corners .

The regular decagon is also dealt with. It has sides of equal length and its corners lie on a common perimeter.

The only possible star (green) with the Schläfli symbol {10/3, 10/7} inscribed on this decagon is called a decagram .

Formulas

Mathematical formulas for the regular decagon
Area	${\ displaystyle A = {\ frac {5} {2}} \ cdot {\ sqrt {5 + 2 {\ sqrt {5}}}} \ cdot a ^ {2} \ approx 7 {,} 694 \ cdot a ^ {2}}$
Length of the diagonal	${\ displaystyle d_ {2} = {\ frac {1} {2}} \ cdot {\ sqrt {10 + 2 {\ sqrt {5}}}} \ cdot a \ approx 1 {,} 902 \ cdot a}$
	${\ displaystyle d_ {3} = {\ frac {1} {2}} \ cdot {\ sqrt {14 + 6 {\ sqrt {5}}}} \ cdot a \ approx 2 {,} 618 \ cdot a}$
	${\ displaystyle d_ {4} = 2 \ cdot r_ {i} = {\ sqrt {5 + 2 {\ sqrt {5}}}} \ cdot a \ approx 3 {,} 078 \ cdot a}$
	${\ displaystyle d = 2 \ cdot r_ {u} = (1 + {\ sqrt {5}}) \ cdot a \ approx 3 {,} 236 \ cdot a}$
Inscribed radius	${\ displaystyle r_ {i} = {\ frac {1} {2}} \ cdot {\ sqrt {5 + 2 {\ sqrt {5}}}} \ cdot a \ approx 1 {,} 539 \ cdot a}$
Perimeter radius	${\ displaystyle r_ {u} = {\ frac {1 + {\ sqrt {5}}} {2}} \ cdot a \ approx 1 {,} 618 \ cdot a}$
Central angle	${\ displaystyle \ alpha = {\ frac {360 ^ {\ circ}} {10}} = 36 ^ {\ circ}}$
Interior angle	${\ displaystyle \ delta = 180 ^ {\ circ} - \ alpha = 144 ^ {\ circ}}$

Calculation of the area

The area of a regular decagon with the side length is calculated as follows: ${\ displaystyle A}$ ${\ displaystyle a}$

{\ displaystyle A = {\ frac {10 \ cdot a ^ {2}} {4}} \ cdot \ cot \ left ({\ frac {\ pi} {10}} \ right) = {\ frac {5} {2}} \ cdot {\ sqrt {5 + 2 {\ sqrt {5}}}} \ cdot a ^ {2} \ approx 7 {,} 694 \ cdot a ^ {2}}

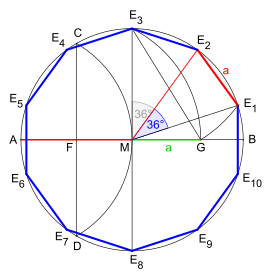
Construction of a decagon

Regular decagon,
alternative construction according to Euclid

A regular decagon can be constructed with a compass and ruler .

Construction for a given perimeter

Construct a regular pentagon (central angle = 72 °), according to the construction with compass and ruler with a given circumference . ${\ textstyle {\ frac {360 ^ {\ circ}} {5}}}$

Draw a line from each corner of the pentagon through the center point of the circle made in step 1 to the other side of the same circle.

The five corners of the pentagon define every other corner of the decagon. The remaining five corners are the points that were constructed by step 2 on the other side of the circle .

A possible alternative to the procedure described above is the following:

Make the construction steps to a pentagon only so far, until the side length of the route E ₃ G is determined. The vertices E ₃ and E ₈ result in the vertical axis of the axis cross .
Transfer the pentagon side E ₃ G determined in this way to the circumference , the first corner point E _{1 of} the decagon being created results.
Halve the angle E ₁ ME ₃ (central angle of a pentagon), the result is the second corner point E ₂ and thus the first side E ₁ E _{2 of} the decagon.
Determine the remaining corner points by subtracting the distance E ₁ E ₂ on the circumference in an anti-clockwise direction.
Connect the neighboring corner points to each other, so the decagon is completed.

Construction for a given side length

Regular decagon with a given side length, see animation

Denote the endpoints of side length a with E ₁ and E ₁₀
Draw an arc around E ₁ with radius E ₁ E ₁₀ through E ₁₀ .
Construct a perpendicular to side length a from E ₁ until it intersects the circular arc around E ₁ in A.
Draw an arc around E ₁₀ with the radius E ₁ E ₁₀ through E ₁ , the points of intersection B and C.
Draw a straight line from C through B ( center perpendicular ), it cuts the side length a in D.
Extend the side length a from E ₁ .
Draw an arc around D with the radius AD until it intersects the extension of the side length a in F.
Draw an arc around E ₁₀ with the radius E ₁₀ F , it intersects the center perpendicular of E ₁ E ₁₀ in the center M of the circumference of the decagon you are looking for.
Draw the circumference of the resulting decagon around M with the radius R = ME ₁₀ .
Determine the remaining corner points by subtracting the side length a on the circumference in an anti-clockwise direction.
Connect the neighboring corner points to each other, so the decagon is completed.

The central angle with the angular width results from the interior angles of the right triangle with the sides and (see next section The golden ratio in the decagon ) according to the Pythagorean theorem : ${\ displaystyle \ mu}$ ${\ displaystyle {\ tfrac {360 ^ {\ circ}} {10}} = 36 ^ {\ circ}}$ ${\ displaystyle {E_ {10} DM}}$ ${\ displaystyle {\ tfrac {a} {2}} = {\ tfrac {1} {2}}}$ ${\ displaystyle R = {\ overline {E_ {10} F}} = {\ tfrac {1 + {\ sqrt {5}}} {2}}}$

{\ displaystyle \ arcsin \ left ({\ frac {\ mu} {2}} \ right) = {\ frac {\ frac {a} {2}} {R}} = {\ frac {\ frac {1} {2}} {\ frac {1 + {\ sqrt {5}}} {2}}} = {\ frac {1} {1 + {\ sqrt {5}}}} = 18 ^ {\ circ}, }

it follows

{\ displaystyle \ mu = 36 ^ {\ circ}.}

The golden ratio in the decagon

Both in the construction with a given circumference as well as in the given side length, the golden ratio is the decisive component by means of external division .

In the construction, given a given circumference, the arc extends with the radius | FE ₃ | around the point F the radius AM around the distance MG . The segment AG thus generated divides the center point M in the golden section .

{\ displaystyle {\ frac {\ overline {AM}} {\ overline {MG}}} = {\ frac {\ overline {AG}} {\ overline {AM}}} = {\ frac {1 + {\ sqrt {5}}} {2}} = \ Phi \ approx 1 {,} 618 {\ text {.}}}

In the construction with a given side length, the circular arc around point D with radius | DA | an extension of the given side length E ₁ E ₁₀ by the distance E ₁ F , so that the distance E ₁₀ F is the longer distance of the ratio (see also derivation of the numerical value ).