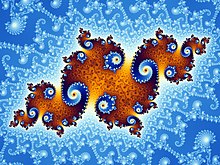
Self-likeness
Self-similarity in the narrower sense is the property of objects, bodies, quantities or geometric objects to have the same or similar structures on a larger scale (i.e. when enlarged) as in the initial state. This property is examined, among other things, by fractal geometry , since fractal objects have a high or perfect self-similarity. The Mandelbrot set is strictly and unlike often not even like to read opinions: Generally, one each cutout of the frame in any magnification view with sufficient resolution, from which point he comes.
In a broader sense, the term is also used in philosophy as well as the social and natural sciences to denote fundamentally recurring structures that are nested in themselves.
Fractal geometry

Of exact (or strict ) self-similarity is the speech, when repeatedly receive the original structure at infinite magnification of the examined object without ever obtaining an elementary fine structure. Exact self-similarity can practically only be found in objects generated mathematically (e.g. by an iterated function system ). Examples are the Sierpinski triangle , the Koch curve , the Cantor set or, trivially, a point and a straight line .
The Mandelbrot set and the Julia set are self-similar, but not strictly self-similar. Strict self-similarity implies scale invariance and can be quantified with the help of the characteristic exponents of the underlying power law ( scale law ).
nature
Real existing examples would be e.g. B. the ramifications of blood vessels , fern leaves or parts of a cauliflower (this is very clear in the Romanesco variety), which are very similar to the cauliflower head in a simple enlargement. In real examples, of course, the enlargement cannot be continued to infinity , as is the case with ideal objects.
Any images of the real world also have self-similarities, which z. B. be used in the fractal image compression or the fractal sound compression .
The recurrences denote the call or the definition of a function by themselves, which are consequently self-similar.
Self-similarity is a phenomenon that often occurs in nature. A characteristic number for the recurring self-similarity is the golden ratio .
The trajectories of a Wiener process and the broken Brownian movement are also self-similar.
literature
- Henning Fernau: Iterated functions, languages and fractals . BI Wissenschaftsverlag, Mannheim - Vienna - Zurich 1994, ISBN 3411170115 .
Web links
- Landscape photos on the scale problem ( memento from January 20, 2014 in the Internet Archive )