Koch curve
The Koch curve or Koch curve is an example presented by the Swedish mathematician Helge von Koch in 1904 for a curve that is constant everywhere but nowhere differentiable . It is also one of the first formally described fractal objects. The Koch Curve is one of the most cited examples of a fractal and was called the Monster Curve when it was discovered . The Koch curve is also known in the form of the Koch snowflake, which is created by a suitable combination of three Koch curves.
construction
The curve can be clearly constructed using an iterative process (see Lindenmayer system ). At the beginning the curve consists of a single stretch. The iteration now consists in replacing this route section with another route section consisting of four equally long routes, which is structured as follows: route - 60 ° angle - route - 120 ° angle (in the opposite direction) - route - 60 ° angle distance. Each of the four new sections is 1/3 the length of the original section. In the next step, each of the four route sections is replaced by a route section of the type above.
This iteration can now be repeated as often as required, with the triangles always being built on the same side of the curve. In this way there is a series of routes that tends towards the Koch curve.
Graphic representation of the construction
The first three iterations of construction
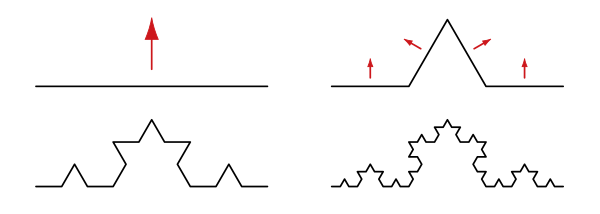
After five iterations:
This construction principle, in which each section is iteratively replaced by a section, can also be used to generate other fractal curves. For example, it is used on the kite curve .
The construction principle is closely related to that of generating the Cantor set , which is obtained if the middle third of the line is not replaced but removed.
Lindenmayer system
The Koch curve can be described by a Lindenmayer system with the following properties:
- Angle: 60 °
- Start string:
- Derivation rules:
If you choose the starting string (an equilateral triangle), you get the Koch snowflake.
Definition of the limit value
The limit value of this iteration (e.g. as an IFS fractal ), the actual Koch curve, is infinitely finely structured in a certain sense and can therefore only be represented graphically as an approximation. In this case, the limit can be easily defined as follows:
- The limit value of the iteration includes those points which are contained in all subsequent iterations from any iteration step on, as well as all accumulation points of the point set thus formed.
For example, the left end point of the initial section is included in every iteration and thus belongs to the cooking curve. The midpoint of the initial section, however, is no longer included from the first iteration. Another (equivalent) limit value definition is given below by the parameter representation .
properties
Properties from fractal geometry
The Koch curve is strictly self-similar according to its construction specification , that is, the same structures appear again and again with any enlargement. It has a Hausdorff dimension of
Length and area
The length of the curve is unlimited, as the route becomes longer by a factor of 4/3 with each iteration step. After the -th iteration step, the curve length has increased by a factor of.
The area “below” the curve (colored green above), however, is limited. If the triangle below the first iteration has the area 1, in the second iteration a triangle with an area of 1/9 is added to each of the 4 lines, and in the -th iteration an area of is added. The entire surface area is accordingly calculated as a geometric series to
- .
Continuity and differentiability
The curve is constant everywhere , but nowhere differentiable .
To investigate these properties, one considers the parametric representation of the -th iteration and its limit function . If you take it as a point in time, the point on the route after the -th iteration is that you reach at the point in time when you run through the route at constant speed (but with abrupt changes in direction) from the left to the right end point. The functions are all continuous and converge pointwise to the limit function .
If you represent the point in time in a development to base 4, i. H. with the digits 0, 1, 2, 3, then the first decimal place indicates the section of the first construction step on which is located, the second the sub-section on this in the second construction step, etc. This allows you to use the first decimal places an area of the order of magnitude construct in which all of the following points must be located. It follows from this property that the functions even evenly to converge. According to one theorem of analysis, the "uniform limit of continuous functions" is then also continuous.
In every section of the curve, no matter how small, there are sections that have a direction for each . Therefore you cannot construct a tangent to any point on the curve, i.e. H. the curve is nowhere differentiable.
Koch's snowflake
If you start the process of replacing the Koch curve not with a segment, but with an equilateral triangle, you get Koch's snowflake . It consists of three Koch curves and, despite its infinite length, only includes an area with a finite area. In contrast to the Koch curve, the Koch snowflake is not self-similar .
application
- One example is the fractal antenna
First publications
- Helge von Koch: Une courbe continue sans tangente, obtenue par une construction géometrique élémentaire . In: Arkiv för Matematik . tape 1 , 1904, p. 681-704 .
- Helge von Koch: Une méthode géométrique élémentaire pour l'étude de certaines questions de la théorie des courbes planes . In: Acta Mathematica . tape 30 , 1906, pp. 145-174 .
Web links
- Further representations
- John J. O'Connor, Edmund F. Robertson : Niels Fabian Helge von Koch. In: MacTutor History of Mathematics archive .
- Eric W. Weisstein : Chef Snowflake . In: MathWorld (English).












![f_ {n} \ colon [0,1] \ to {{\ mathbb R}} ^ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e140c9bb26a5999a48febfbe79bdd7002f41baec)

![t \ in [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)










