interest rate
The interest rate (including interest rate ) is in the economy in percent expressed Price for money or capital (with interest-linked financial products such as loans or investments ) expressed as a percentage of the interest rate .
General
The words “interest” or “interest rate” appear frequently in laws , but there is no legal definition because they are generally assumed to be known. The BGB, for example, speaks in Section 247 (1) BGB that the reference value for the base rate is “the interest rate for the most recent main refinancing operation of the European Central Bank before the first calendar day of the relevant half-year”. In § 188 BewG it is mentioned that the property interest rate is the interest rate "at which the market value of real estate is on average subject to market interest". For example, the everyday term “rent” for rent , which the BGB itself does not use, is factually incorrect ; it simply speaks of “rent” (for example in Section 535 (2) BGB).
Size symbols
In the specialist literature on interest and interest rates, common symbolic terms are p , i (from English interest ) and r (from English rate ).
Interest rate and rate of interest
In financial mathematics , a precise distinction is made between interest rate i and interest rate p . While the interest rate directly measures the ratio of “interest through capital” - usually as a percentage - the rate of interest is the corresponding indication in hundred parts - this corresponds to the number in front of the percentage sign in the indication of the interest rate. So it applies
- .
Example: With an interest rate of i = 5%, the interest rate is p = 5. The conversion in both directions is as follows in this example:
- .
Calculation methods
General interest formula
With
- Z : interest income
- K : capital in monetary units
- i : interest rate
- p : rate of interest
- t : compounding period in days
- T : Daily divider (annual assessment basis).
Assessment base of the interest rate i
The interest rate is usually based on a year (p. A., Per anno / per annum ). In addition, there are also monthly interest rates p. M. per mese and those by quarter ( p. Qu ) before.
Bank year: Usages of the time units t / T
For the correct use of the interest formula with regard to days t and day divider T, it is always important to specify the interest calculation method . These usages are commonly called the banking year . This means the convention of how many days a year is to be calculated.
The interest calculation method indicates how to proceed with terms of less than one year. There are the following methods:
- 30/360 (German method)
- The year is calculated with 360 days, each month with 30 days.
- act / 360 ( Euro method or French usage )
- The year is calculated with 360 days, with the month the actual days count ( actual , German klm , calendar-wise).
- act / 365 (English method)
- The year is considered excessive calendar common year expected 365 days, the monthly count the actual days (actual) .
- act / act (exact day method)
- Both the year and the month are calculated with the actual days (actual) . The interest period is split up if leap years are included, and the associated divisors are used for each part. (Example: December 20, 2007 to January 20, 2008: 31 days, divided into 11 days / 365 and 20 days / 366).
The act / 360 method is now common on the money markets in the Eurozone .
Normally, the first day (the day on which interest business is started) is not included.
An example is an interest rate of i = 5% = 0.05 and a capital amount of k = 100,000.00 euros. The money is invested from February 15, 2008 to March 15, 2008 (a leap year ) (investment entry on February 14, 2008). This results in the following interest payments for the interest calculation methods:
- 30/360 :
- act / 360 :
- act / 365 :
- act / act :
Compound interest effect: Annual and continuous interest rate
A simple calculation example shows the influence of the compound interest effect on the result:
- If you invest one euro for one year at an interest rate of 100 percent and the interest is credited annually, you would receive € 1 credit + € 1 interest = € 2 at the end of this one year. With an interest credit every 6 months, on the other hand, 0.5 € interest is credited after half a year for the first euro and after a further six months a further 0.75 € for the total of interest from 1.5 €. In the end you have a total of 1 € credit + 1.25 € total interest = 2.25 €. With a monthly distribution you will receive 2.61 € after one year. If the interest is credited and compounded at ever shorter intervals, the payout amount in this example tends towards the limit of e €, i.e. approximately 2.718282 €. Refers here to e the Euler's number .
Each interest rate from continuous interest corresponds to an interest rate with annual interest (per annum, abbreviated p. A.) According to the following formula:
For example, an annual interest rate of 20% corresponds to a continuous interest rate of around 18.23%.
For periods that deviate from one year, it is often cheaper to calculate with interest rates in continuous compounding. Hourly billing is not common in banking.
Types of Interest Rates
In particular, there are different types of interest rates:
- Nominal interest rate : Pure interest rate with which the interest amount is calculated
- Real interest rate : A nominal interest rate adjusted for the effects of inflation
- Effective interest rate : an interest rate calculated after taking into account the disbursement rate , additional costs and inter-period interest payments
- Reference interest rate : An interest rate determined daily by a neutral body across all institutions for a certain currency and term .
Basic interest rates for the economy as a whole are:
- Base rate for interbank loans
- Base interest rate for savings deposits .
The following term only refers to the amount of the interest rate and can be applied to any type of interest rate:
- Negative interest : Any interest rate that is less than zero (example: −0.88%).
Fixed rate and variable rate
Under fixed-rate refers to an interest rate that remains unchanged constant for a certain period of time, regardless of the current market trend of market interest rates . A legal definition is provided by Section 489 (5) BGB , according to which a “tied” interest rate is agreed as a fixed percentage for the entire term of the contract. A fixed interest rate can either be agreed for the entire term of a loan or an investment or only for part of the term (see fixed interest period ). A variable interest rate is an interest rate that adapts to the current market situation. Arbitrary interest rate structures are not permitted for contracts with variable interest rates. Rather, a reference interest rate is to be contractually determined, which takes into account the individual contract structure and is accessible in public media . The time series database of the Deutsche Bundesbank is ideal for this.
Internal rate of return
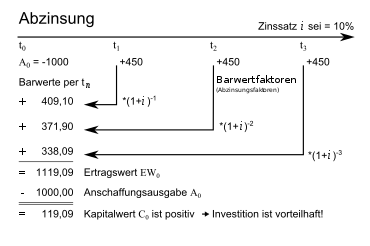
The internal rate of return is the rate at which the net present value of a series of payments or a project is by definition exactly zero. With the help of the internal rate of return method, it can be concluded from this whether the implementation of this project is advantageous or not. The project is always advantageous - and therefore delivering a positive net present value - when the discount rate is lower than the internal rate, and disadvantageous when the discount rate is higher. Also known as the effective interest rate (for financing) or the internal rate of return (IRR) .
Discount rate
The discount rate or discount rate (Engl. Hurdle rate or required rate of return ) is in the capital budgeting at discounted cash flow used analyzes. It describes the subjective minimum rate of interest an investor demands on his investment and determines how much further future payments are devalued to their present value . The discount rate is determined by increasing (investment) or decreasing (lending) the cost of capital or weighted capital costs by a risk premium .
Taking the time value of money into account , it becomes clear that the demand for a high return is synonymous with the demand for riskier and shorter-term investments, since payments that are close to the present are valued more strongly than later payments.
See also
Web links
Individual evidence
- ^ Wolfgang Breuer, Claudia Breuer, Jürgen Weber, Ulrich Pape: Zinsfuß. In: Gabler Wirtschaftslexikon. Springer Gabler Verlag, accessed February 25, 2017 .
- ^ BGH, judgment of February 17, 2002, Az .: XI ZR 140/03 = BGHZ 158, 149
- ^ BGH, judgment of April 13, 2010, Az .: XI ZR 197/09 = BGHZ 185, 166
- ↑ Deutsche Bundesbank , Deposit and Lending Rates , 2019