Interest bill
The interest calculation describes a mathematical procedure for calculating interest that is charged as consideration on borrowed amounts of money .
Basically, the interest calculation is divided into the "simple interest calculation", in which the accruing and unpaid interest and the amount of money to be interest-bearing, e.g. B. credit , loan or savings, are not added, and the compound interest calculation , in which unpaid interest is added to the basic amount and taken into account in the further interest.
Furthermore, according to the number of interest periods (interest payments) in the year, a distinction can be made between annual (one-time interest) and inter-annual interest (multiple interest), as well as the special case of continuous interest. The standard case is the annual interest rate: The capital is paid once a year, usually at the end of the year. The interest rate following the interest period is referred to as decursive , the advance rate as anticipatory .
If a deposit is paid into or withdrawn from a savings account within the interest period, the mixed interest rate is generally used by financial companies. This type of interest is therefore also used for all investments with a term that is not a multiple of the interest period (for example 3.5 years with annual interest). This is referred to as a broken term.
While the interest calculation is generally based on a one-off paid in or borrowed amount or initial capital, the sub-area of the pension calculation is conversely primarily concerned with regularly recurring payments in and out, with both aspects ultimately merging in the form of the amortization calculation , for example if on a one-off basis The disbursement of a loan is then followed by a series of more or less regular payments, with which this loan is "paid off" again, ie is repaid.
Preliminary remarks
The interest calculation formulas in this article use the following symbols:
- Initial capital: (capital after 0 years)
- Final capital: (capital after years)
- Duration (whole years): Entry in years
- Duration (days): Entry in days
- Interest rate in percent: (per interest period)
- Interest rate as a decimal: (per interest period)
- Interest rate as interest factor: (per interest period)
Depending on the calculation method , the year fluctuates between 360 and 366 days, the month between 28 and 30 to 31 days. E.g. 7% interest rate for the term of 360 days.
Annual interest
Simple interest without compound interest (linear interest)
In the case of annual interest, this applies to the final capital
Through transformation, formulas are obtained for calculating the starting capital, interest rate or the term required for a specific final capital:
example
A start-up capital of € 1,000 is invested at an interest rate of 5 percent over 2 years. With simple interest, the final capital would be
Compound interest calculation (exponential interest rate)
The formula for the capital after years with annual interest and compound interest is:
The formula can be changed to determine the starting capital, the interest rate or the term given the final capital:
Examples
A start-up capital of € 1,000 is invested at an interest rate of 5 percent over 2 years. With annual interest the final capital would be
Final value / final capital / present value
A start-up capital of € 1,000 is paid at an interest rate of 5% p. a. laid out over 2 years. With compound interest there is a final capital of
- .
If you are looking for the term after which the start-up capital has doubled , the following generally applies:
This value can also be estimated using the rule of 72 .
If, conversely, a given final value is calculated back to the starting capital that would be necessary to achieve the final value for a given term and a given interest rate, this value is called the present value of the final value or capital:
In words: To get 1,100 € in 2 years from a 5% p. a. To be able to withdraw interest-bearing account, you would have to pay 997.73 € to this account at the present time, in other words, 1.100 € in 2 years will be worth practically as much as this amount in cash today.
Interest within the year
Interest is credited several times a year for investments that bear interest during the year. The period of interest is therefore less than a year. For example, periods of:
- half a year,
- a quarter or
- a month or
- on a daily basis with remaining months.
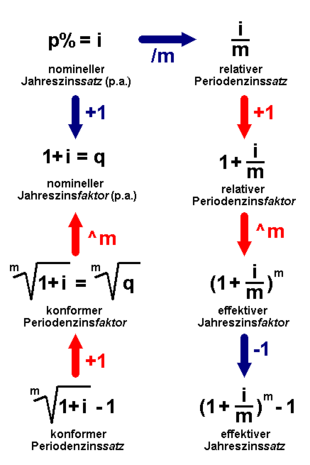
The number of interest periods in the year is expressed in formulas by the symbol . For example, quarterly interest would be 4 (4 quarters per year). A so-called nominal annual interest rate ( ) is often given.
The relative period interest rate is then:
- .
The formulas for the interim interest rate are then to be used as described above; the interest rate is no longer valid per year, but per interest period. The term is also not specified in years, but in interest periods.
Simple interest (linear)
The following applies to the final capital after years with each interest period and further interest periods during the year:
- .
It represents the total number of interest periods according to years and periods (term in interest periods).
example
A capital of € 1,000 is invested with monthly interest ( ) at a nominal annual interest rate of 6 percent.
The relative period interest rate is 0.5%. After 2 years and 4 months with simple interest a final capital of
Compound interest (exponential)
The following applies to the final capital after years with each interest period as well as further interest periods during the year
- .
The term in interest periods is calculated again in the same way as the simple interest calculation .
In addition to the relative and nominal interest rate can be at compound interest case, the effective year interest rate determine in which a one-time annual interest rate on this very same result as a repeated intra-year interest rate on the relative interest rate. With as the nominal annual interest rate p. a., as the number of interest periods per year and the quotient of both variables as the relative period interest rate then applies:
- .
If you multiply the brackets and leave out the higher powers of (which contribute almost nothing to the sum for small ones), you can estimate the effective interest well:
- .
The additional interest gain with multiple interest payments during the year compared to the one-off annual interest can thus be estimated as follows:
- .
If only the effective interest rate is given, then the relative period interest rate, in this case also referred to by some authors as the "conforming" interest rate , results from the following formula:
- .
Regarding the term “conforming” interest rate or rate of interest just mentioned, this is unfortunately used in the literature, like that of the “effective” interest rate, in several ways that are not always easily distinguishable from one another, which easily leads to confusion and misunderstandings. The decisive factor in all cases is what is chosen as the reference point for the "conforming" interest rate, i. H. with which this interest rate should be “conform” or what it should be “equivalent” or “equal in value”.
So he is from individual authors, but z. For example, SAP in their banking software is equated with the effective annual interest rate as a compliant annual interest rate, but in most cases only defined on the basis of this or the nominal annual interest rate.
If the "conforming" interest rate or rate is defined according to the following formula only on the basis of the effective annual interest rate, without equating it with it, it ultimately turns out to be nothing other than the already mentioned relative periodic interest rate:
- .
This "conforming" interest rate is therefore the interest rate that, with m-fold geometric or exponential interest rates at the end of the year, delivers the same result as the simple application of the effective annual interest rate :
- .
In order to avoid misunderstandings, the “conforming” interest rate defined in this way should therefore be described more precisely as the (equivalent) intra-year interest rate that conforms to the effective annual interest rate - or, instead, preference should be given from the outset to the concept of the relative periodic interest rate with the same meaning .
The other part of the vast number of authors, however selected as reference point for the definition of "compliant" interest rate instead of the effective the nominal year interest rate
- .
The “conforming” interest rate is now - unlike before - the interest rate which, with m-fold geometric or exponential interest rates at the end of the year, delivers the same result as the simple application of the nominal annual interest rate
- ,
which is why it is also referred to by some authors as - one should add “at the nominal annual interest rate” - conforming (equivalent) intra- year or periodic interest rate.
example 1
A capital of € 1,000 is invested as above ; , .
After 2 years and 4 months and thus 28 times geometric or exponential interest with the relative period interest rate, the capital including compound interest is then
- .
The same result would also be obtained if one used the effective annual interest rate from the start , in this case
- ,
would calculate:
- .
However, would in the same way, only this time with the (for nominal year interest rate) compliant periods interest rate interest that 28 months would result after only a capital incl. Compound interest of
- .
Example 2
A capital of € 10,000 is invested annually.
With an annual interest rate ( ), the capital with interest after one year is:
is the effective interest rate .
With a quarterly interest rate ( ) during the year , the capital with interest after one year is:
The additional interest gain with quarterly interest compared to the annual interest is
- .
and can be estimated with:
- .
With monthly interest payments ( ) during the year , the capital with interest after one year is:
The additional interest gain with a monthly interest compared to the annual interest is
- .
and can be estimated with:
- .
With a steady interest rate during the year ( see below), the capital with interest after one year is:
The additional interest gain with constant interest compared to the annual interest is
- .
and can be estimated with:
- .
An investment with an annual one-off interest rate of z. B. 3.05% would therefore always result in a higher interest income than a financial investment with a nominal interest rate of only 3.00% and any more frequent interest payments during the year. Many financial institutions, on the other hand, advertise the higher interest income with a year-on-year, e.g. B. Quarterly interest without precisely quantifying the higher interest income. In the example above, it is easy to see that the quarterly interest paid during the year for an investment of € 10,000 only provides a minimal additional interest income of € 3.39, and even in the ideal case of constant interest it would not be more than € 4.55.
Mixed interest
Banks and other financial companies usually credit current accounts and savings books with the interest at the end of the interest period. In the case of savings books and other current accounts, this is usually the end of the year, in the case of contractually agreed investments it is often a different time.
Although compound interest calculation is actually used, capital that was not invested at the last interest clearing time and therefore not for the entire interest period bears interest with simple interest, just like on a payment date within the interest period that accrued in the year up to that point.
The following diagram shows a typical investment: the investment falls on any day of the year, the capital earns interest for a few years and is finally paid out on any day within the year.
The entire investment period is made up as follows:
- .
First, interest is paid on the capital over the remaining period of 1 ( days) with simple interest. The capital obtained in this way pays interest over the years according to the compound interest formula. The remaining period 2 ( days) is then simply paid interest again from the capital at the end of the nth year. In summary, the following formula results for the capital on the payment date:
- According to the German interest calculation method, 360 days are set for the year (see the corresponding section in the interest rate article ).
In the case of broken investment periods, the value date practice of the banks must be observed: In Germany, the investment day is usually included in the case of savings balances, but interest is no longer paid on the day of payment. Otherwise - z. B. for sight and time deposits - conversely, interest is paid on the payment date, but not on the payment date.
In the case of interest payments during the year, you proceed in the same way and change the reference period accordingly (e.g. in quarters, 90 instead of 360 in the denominator).
example
On June 25, 2008, € 1,000 will be invested in a savings account at an interest rate of 2.5%. What is the payout amount if the savings book is closed on April 12, 2013?
According to the German interest calculation method, days will pass until the end of 2008 . The capital is fixed for the entire years 2009–2012 ( ). In 2013, interest is still paid for days.
The capital on the payment date is therefore
The calculation of simple interest benefits the investor: if compound interest were calculated over the entire term, one would get in the present case
- .
Continuous interest
The constant interest rate is a special case of the exponential interest rate during the year (with compound interest), in which the number of interest periods tends towards infinity (also instantaneous interest or continuous interest ). The period of the individual interest period therefore approaches 0.
The following applies to the final capital after years with an interest rate :
A start-up capital of € 1,000 is invested at an interest rate of 5 percent over 2 years. With constant interest, the final capital would be
One of the advantages of steady interest is that you don't have to worry about the interest capitalization, since capitalization takes place almost at any time. This means that constant interest is often the basis of financial mathematical models, as this type of interest is particularly easy to use. A well-known example of this is the Black-Scholes model .
See also
- Annuity
- Annuity loan
- Josephspfennig
- Installment loan
- Pension bill
- Savings bank formula
- Hardy rate formula
- Interest numbers
Web links
- Derivation of the formula for the continuous interest rate
- Overview of different interest methods, i.e. interest days per month or year as well as the start and end of interest
Individual evidence
- ↑ Effective interest calculation - effective interest rate , last accessed August 17, 2016.
- ↑ Joseph Leydold: Mathematical Methods in Economics. Basic course. Chapter 1: Returns ; WU Vienna, SS 2006 , last accessed August 18, 2016.
- ↑ SAP: Compound interest calculation during the year , last accessed August 17, 2016.
- ^ Alfred Brink: Finanzmathematik. Chapter C. Interest Statements ; University of Münster, p. 31 ( Memento of the original dated December 11, 2015 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. , last accessed August 17, 2016.
- ↑ Jürgen Tietze: Exercise book for financial mathematics, formula appendix 1 (to the basics of classical financial mathematics) ; Wiesbaden 2011, pp. 422–423 [available as PDF, but without a fixed link ].
- ^ Wolfgang Blaas: Finanzmathematik - slides for the lecture ; TU Wien, page 12 , last accessed August 17, 2016.
- ^ Collection of formulas for financial mathematics ; FH Düsseldorf , last accessed August 18, 2016.
- ^ Jutta Gerhard: Interest, compound interest and pension calculation ; VHS Floridsdorf , last accessed August 18, 2016.
- ↑ Effective interest calculation - Relative and conforming periodic interest rate , last accessed August 17, 2016.
- ↑ Conforming period interest , last accessed August 17, 2016.
- ↑ Interest methods and interest law , last accessed on August 18, 2016.













![i = {\ sqrt [{n}] {{\ frac {K_ {n}} {K_ {0}}}}} - 1 \ qquad {\ text {or}} \ qquad q = {\ sqrt [{n }] {{\ frac {K_ {n}} {K_ {0}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b2430671de87addd63d3e4d5b1b06bca4668a07)
![p = \ left ({\ sqrt [{n}] {{\ frac {K_ {n}} {K_ {0}}}}} - 1 \ right) \ cdot 100](https://wikimedia.org/api/rest_v1/media/math/render/svg/36f118c876027b69520c9ae7bbd9220db31b5da6)











![K _ {{{\ mathrm {n, k}}}} = K_ {0} \ cdot (1+ [n \ cdot m + k] \ cdot i _ {{{\ mathrm {rel}}}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/32ff9fc9518d064d30b4a7bf3da94343ecbececb)


![K _ {{{\ mathrm {2,4}}}} = 1000 \; \ mbox {\ euro} \ cdot (1+ [2 \ cdot 12 + 4] \ cdot 0 {,} 005) = 1000 \; \ mbox {\ euro} \ cdot 1 {,} 140 = 1140 \; \ mbox {\ euro}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c891f261f0eb7412c30585738411ec3fe52cf41)







![{\ displaystyle i _ {\ mathrm {rel}} = {\ sqrt [{m}] {1 + i _ {\ mathrm {eff}}}} - 1 = i _ {\ mathrm {kon}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50b3bd724318bd46025344f8917f78e934b887c4)
![{\ displaystyle i _ {\ mathrm {kon}} = {\ sqrt [{m}] {1 + i _ {\ mathrm {eff}}}} - 1 = {\ sqrt [{m}] {1+ (1+ {\ frac {i _ {\ mathrm {nom}}} {m}}) ^ {m} -1}} - 1 = {\ frac {i _ {\ mathrm {nom}}} {m}} = i _ {\ mathrm {rel}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5115699fb3abb62905d6e559ffda8f73b3af6e53)

![{\ displaystyle i _ {\ mathrm {kon}} = {\ sqrt [{m}] {1 + i _ {\ mathrm {nom}}}} - 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4b2a0aa0cf092d4a17153be1039f7e45a8dae7d)



![{\ displaystyle i _ {\ mathrm {rel}} = {\ tfrac {0 {,} 06} {12}} = 0 {,} 005, i _ {\ mathrm {kon}} = {\ sqrt [{12}] {1 {,} 06}} - 1 \ approx 0 {,} 004868)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/807488afc362bdb4482604e3a104a240428698c2)






























![{\ begin {matrix} K & = & \ lim _ {{m \ to \ infty}} \ left [K_ {0} \ cdot \ left (1 + {\ frac {i} {m}} \ right) ^ { {mn}} \ right] \\\\ & = & K_ {0} \ cdot e ^ {{n \ cdot i}} \ end {matrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bf64913b6a4f032b50e8f1c22fef7433f92d38e)
