Fifteenth

Regular fifteen-sided

The pentadecagon or Pentadekagon is a geometric figure , and a polygon ( polygon ). It is determined by fifteen corner points and their fifteen connections called lines , sides or edges.

Variations

The fifteenth corner can be represented as:

• concave fifteen- sided in which at least one interior angle is greater than 180 °. A fifteen corner can have at most seven such angles.
• convex fifteen-sided, in which all interior angles are smaller than 180 °. A convex fifteenth corner can be regular or irregular.
• Chordal pentagon, in which all corners lie on a common perimeter , but the side lengths may be unequal.
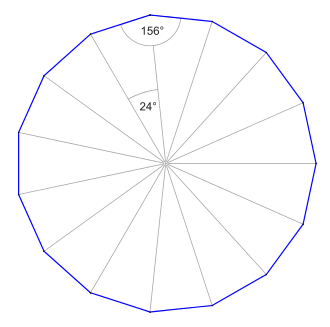
• Regular fifteen-sided: It is determined by fifteen points on a virtual or real circle. The neighboring points are always at the same distance from each other and are connected by strings that are lined up, also called sides or edges .
• Regularly crossed fifteen-corner: This results when at least one is skipped over each time when connecting the fifteen corner points and the chords thus created are of the same length. Such regular stars are noted with Schläfli symbols , indicating the number of corner points and connecting every -th point. ${\displaystyle \left\{n/k\right\}}$ ${\displaystyle n}$ ${\displaystyle k}$

There are only three regular fifteen-ray stars.

The "stars" with the symbols {15/3} and {15/12} are regular pentagons, {15/5} and {15/10} equilateral triangles and {15/6} and {15/9} regular pentagrams .

• Regular fifteen-ray stars
• 

  ${\displaystyle \left\{15/2\right\}{,}\ \left\{15/13\right\}}$

• 

  ${\displaystyle \left\{15/4\right\}{,}\ \left\{15/11\right\}}$

• 

  ${\displaystyle \left\{15/7\right\}{,}\ \left\{15/8\right\}}$

Regular fifteen-sided

According to Carl Friedrich Gauß and Pierre-Laurent Wantzel, the regular fifteen - sided is a constructible polygon , since the number of its sides can be represented as the product of a power of two with pairwise different Fermat's prime numbers ( ). As with the regular pentagon , the golden ratio is the decisive component for a construction with compass and ruler . ${\displaystyle 15=2^{0}\cdot 3\cdot 5}$

Sizes

Sizes of a regular fifteen-sided
Interior angle	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {13}{15}}\cdot 180^{\circ }\\&=156^{\circ }\end{aligned}}}$
Central angle (Center angle)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{15}}\\\mu &=24^{\circ }\end{aligned}}}$
Side length	${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{15}}\right)=2\cdot R\cdot \sin(12^{\circ })\\&={\frac {1}{4}}\cdot R\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\approx 0{,}416\cdot R\end{aligned}}}$
Perimeter radius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{15}}\right)}}={\frac {a}{2\cdot \sin(12^{\circ })}}\\&={\frac {1}{2}}\cdot a\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)\approx 2{,}405\cdot a\end{aligned}}}$
Inscribed radius	${\displaystyle {\begin{aligned}r&=a\cdot {\frac {1}{2}}\cdot \cot \left({\frac {180^{\circ }}{15}}\right)=a\cdot {\frac {1}{2}}\cdot \cot(12^{\circ })\\&={\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\approx 2{,}352\cdot a\end{aligned}}}$
height	${\displaystyle {\begin{aligned}h&=r+R\approx 4{,}757\cdot a\end{aligned}}}$
Area	${\displaystyle {\begin{aligned}A&={\frac {15}{4}}\cdot a^{2}\cdot \cot \left({\frac {180^{\circ }}{15}}\right)={\frac {15}{4}}\cdot a^{2}\cdot \cot(12^{\circ })\\&={\frac {15}{8}}\cdot a^{2}\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\approx 17{,}642\cdot a^{2}\end{aligned}}}$

Mathematical relationships

Interior angle

The general formula for polygons gives:

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {15-2}{15}}\cdot 180^{\circ }={\frac {13}{15}}\cdot 180^{\circ }=156^{\circ }}$

This value can also be derived from the following considerations:

The fifteen corner can be divided into fifteen triangles, the sides of which are each one side of the fifteen corner and the connecting lines of its center point with the two end points of the side. The angles at the midpoint of the fifteenth add up to its central angle . Since the sum of the angles in a triangle is always and the triangle is isosceles and therefore symmetrical to the bisector of the central angle, the two unknown angles each include . Since this applies to all fifteen triangles, the two angles add up at a corner point . ${\displaystyle a}$ ${\displaystyle 360^{\circ }{\text{,}}}$ ${\displaystyle 24^{\circ }{\text{.}}}$ ${\displaystyle 180^{\circ }}$ ${\displaystyle {\frac {180^{\circ }-24^{\circ }}{2}}=78^{\circ }}$ ${\displaystyle 156^{\circ }}$

Central angle

The central angle or center angle is enclosed by two adjacent circumferential radii . Enter the number for the variable in the general formula . ${\displaystyle \mu }$ ${\displaystyle R}$ ${\displaystyle n}$ ${\displaystyle 15}$

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{15}}=24^{\circ }}$

Side length and perimeter radius

Again the fifteen-corner is broken down into 15 congruent triangles. If one half of such a triangle, that is a right triangle with sides , and as well with half the central angle so true ${\displaystyle {\frac {a}{2}}}$ ${\displaystyle R}$ ${\displaystyle r}$ ${\displaystyle {\frac {24^{\circ }}{2}}=12^{\circ },}$

${\displaystyle \sin(12^{\circ })={\frac {\frac {a}{2}}{R}}={\frac {a}{2\cdot R}}.}$

It follows from this relationship

${\displaystyle a=2\cdot R\cdot \sin(12^{\circ })\approx 0{,}416\cdot R.}$

If one dissolves, one obtains ${\displaystyle R}$

${\displaystyle R={\frac {a}{2\cdot \sin(12^{\circ })}}\approx 2{,}405\cdot a.}$

Algebraic expressions for or can be found in the sections Calculating the Side Length and Calculating the Radius . ${\displaystyle a}$ ${\displaystyle R}$

Inscribed radius

The incircle radius can also be determined using a halved determination triangle. It turns out ${\displaystyle r}$

${\displaystyle \tan \left(12^{\circ }\right)={\frac {\frac {a}{2}}{r}}={\frac {a}{2\cdot r}}}$.

Multiplying by gives ${\displaystyle 2\cdot r}$

${\displaystyle 2\cdot r\cdot \tan \left(12^{\circ }\right)=a}$

and further

${\displaystyle r={\frac {a}{2\cdot \tan \left(12^{\circ }\right)}}}$

because of

${\displaystyle {\frac {1}{\tan \left(12^{\circ }\right)}}=\cot \left(12^{\circ }\right)}$

also applies

${\displaystyle r=a\cdot {\frac {1}{2}}\cdot \cot \left(12^{\circ }\right).}$

Algebraic expressions for or can be found in the section Calculating the inscribed radius . ${\displaystyle \cot \left(12^{\circ }\right)}$ ${\displaystyle r}$

height

The height h of a regular fifteen-corner is the sum of the inner and circumferential radius, since the extension of the height of a section beyond the center of the fifteen-corner meets a corner point.

${\displaystyle h=R+r={\frac {a}{2\cdot \sin(12^{\circ })}}+{\frac {a}{2\cdot \tan(12^{\circ })}}\approx 4{,}757\cdot a}$

Area

The area of ​​a triangle is calculated as . For one of the 15 determination triangles, the height is equal to the inscribed radius . The area of ​​the entire fifteen-sided is therefore ${\displaystyle A_{\Delta }={\frac {1}{2}}\cdot a\cdot h_{a}}$ ${\displaystyle h_{a}}$ ${\displaystyle r}$

${\displaystyle A={\frac {15}{2}}\cdot a\cdot r.}$

Together with the expression for derived in the calculation of the inscribed radius , it follows from this ${\displaystyle r}$

${\displaystyle A={\frac {15}{2}}\cdot a\cdot {\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)={\frac {15}{8}}\cdot a^{2}\cdot \left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\approx 17{,}642\cdot a^{2}}$

Construction with compass and ruler for a given circumference

In the construction shown here, an equilateral triangle (steps 1–3) and the first four points of a regular pentagon (steps 4–6) are fitted into the given circumference. is then the side of a regular fifteen-corner in the given circumference. This type of construction was already described by Euclid in his work Elements (The Stoicheia) in Book IV; however, the construction details of the triangle and pentagon differ from its construction. The determination of the first side of the fifteen-sided corresponds to the representation of Johannes Kepler . ${\displaystyle BE_{1}E_{6}}$ ${\displaystyle BE_{14}E_{2}E_{5}E_{8}}$ ${\displaystyle {\overline {E_{1}E_{2}}}}$

${\displaystyle {\overline {AB}}}$denotes the distance between points and ${\displaystyle A}$ ${\displaystyle B{\text{.}}}$

Construction sketch		Animation of the sketch

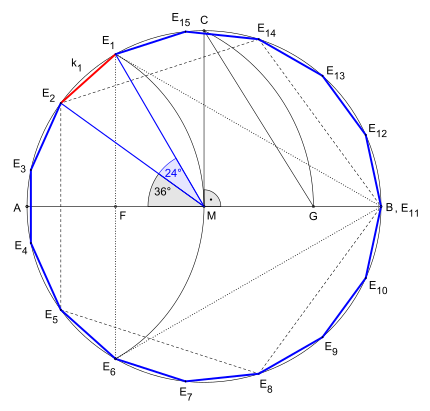
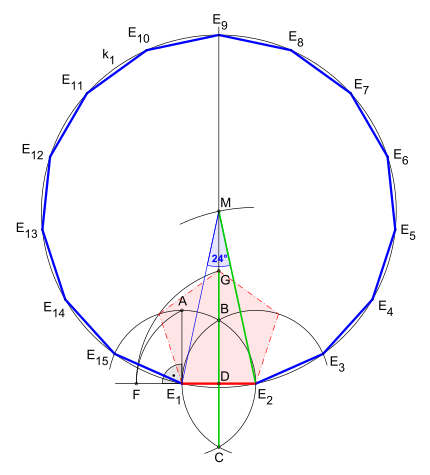
If there is a circle k ₁ (the circumference around the resulting fifteen corner) around the center point M, a regular fifteen corner can be constructed by:

1. Drawing a diameter; A and B are intersections with k ₁
2. Construction of a radius orthogonal to AB ; The point of intersection with k ₁ is C
3. Construction of an arc around A with radius AM ; Points of intersection with k ₁ are E ₁ and E ₆
4. Drawing E ₁ E ₆ ; The intersection with AB is F
5. Draw an arc around F with radius FC ; The point of intersection with AB is G
6. four times the distance CG is removed on k ₁ from B in a counterclockwise direction; Points of intersection with k ₁ are E ₁₄ , E ₂ , E ₅ , and E ₈ ; the connection of the corner points E ₁ with E ₂ results in the first side of the resulting fifteen- corner
7. eight times removal of the tendon E ₁ E ₂ from k ₁ to k ₁ from E ₂ counterclockwise; the points of intersection with k ₁ are the remaining corner points E ₃ , E ₄ , E ₇ , E ₉ , E ₁₀ , E ₁₂ , E ₁₃ and E _{15 of} the fifteen-triangle
8. Connect the points found in this way.

Calculation of the side length

The formula for the side length given in the table above is derived as follows: ${\displaystyle a={\frac {1}{4}}\cdot R\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)}$

${\displaystyle {\mathsf {(1)}}}$ Equilateral triangle ${\displaystyle AME_{1}}$

${\displaystyle {\mathsf {(1.1)}}\;{\overline {ME_{1}}}=R}$ (Perimeter radius)

${\displaystyle {\mathsf {(1.2)}}\;{\overline {AM}}={\overline {ME_{1}}}={\overline {AE_{1}}}=R}$ after construction, step 3

${\displaystyle {\mathsf {(1.3)}}\;{\overline {FM}}={\frac {1}{2}}\cdot R}$

${\displaystyle {\mathsf {(2)}}}$ Right triangle ${\displaystyle \;FME_{1}}$

According to the Pythagorean theorem : ${\displaystyle {\overline {ME_{1}}}^{2}={\overline {FM}}^{2}+{\overline {FE_{1}}}^{2}}$

${\displaystyle {\begin{aligned}(2.1)\;{\overline {FE_{1}}}&={\sqrt {{\overline {ME_{1}}}^{2}-{\overline {FM}}^{2}}}={\sqrt {R^{2}-\left({\frac {1}{2}}\cdot R\right)^{2}}}={\sqrt {R^{2}-{\frac {1}{4}}\cdot R^{2}}}\\&={\sqrt {{\frac {3}{4}}\cdot R^{2}}}=R\cdot {\sqrt {\frac {3}{4}}}=R\cdot {\frac {\sqrt {3}}{2}}\end{aligned}}}$

${\displaystyle {\mathsf {(3)}}}$ Right triangle ${\displaystyle FMC}$

According to the Pythagorean theorem: ${\displaystyle {\overline {FC}}^{2}={\overline {FM}}^{2}+{\overline {MC}}^{2}}$

${\displaystyle {\mathsf {(3.1)}}\;{\overline {FC}}={\sqrt {{{\overline {FM}}^{2}}+{{\overline {MC}}^{2}}}}={\sqrt {\left({\frac {1}{2}}\cdot R\right)^{2}+R^{2}}}={\sqrt {{\frac {5}{4}}\cdot R^{2}}}=R\cdot {\frac {\sqrt {5}}{2}}}$

${\displaystyle {\mathsf {(3.2)}}\;{\overline {FG}}={\overline {FC}}=R\cdot {\frac {\sqrt {5}}{2}}\;}$ after construction, step 5

${\displaystyle {\mathsf {(4)}}}$ Right triangle ${\displaystyle ABE_{2}}$

${\displaystyle \angle ABE_{2}}$denotes the angle enclosed by and : ${\displaystyle {\overline {AB}}}$ ${\displaystyle {\overline {BE_{2}}}}$ ${\displaystyle \beta }$

${\displaystyle {\mathsf {(4.1)}}\;{\overline {MG}}={\overline {FG}}-{\overline {FM}}=R\cdot {\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\cdot R=R\cdot {\frac {{\sqrt {5}}-1}{2}}}$

${\displaystyle {\mathsf {(4.2)}}\;{\overline {AE_{2}}}={\overline {MG}}=R\cdot {\frac {{\sqrt {5}}-1}{2}}\;}$

According to the Thales theorem , the triangle is right-angled, again according to the Pythagorean theorem: ${\displaystyle ABE_{2}}$ ${\displaystyle {\overline {AB}}^{2}={\overline {AE_{2}}}^{2}+{\overline {BE_{2}}}^{2}}$

${\displaystyle {\begin{aligned}{\mathsf {(4.3)}}\;{\overline {BE_{2}}}&={\sqrt {{\overline {AB}}^{2}-{\overline {AE_{2}}}^{2}}}={\sqrt {{(2\cdot R)}^{2}-\left({R\cdot {\frac {{\sqrt {5}}-1}{2}}}\right)^{2}}}={\sqrt {4\cdot R^{2}-{R^{2}}\cdot {\frac {\left({\sqrt {5}}-1\right)^{2}}{4}}}}\\&=R\cdot {\sqrt {4-{\frac {\left({\sqrt {5}}-1\right)^{2}}{4}}}}=R\cdot {\sqrt {{\frac {16}{4}}-{\frac {\left(5-2\cdot {\sqrt {5}}+1\right)}{4}}}}=R\cdot {\sqrt {\frac {10+2\cdot {\sqrt {5}}}{4}}}\\&=R\cdot {\sqrt {{\frac {1}{4}}\cdot \left(10+2\cdot {\sqrt {5}}\right)}}=R\cdot {\frac {1}{2}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}\end{aligned}}}$

${\displaystyle {\begin{aligned}{\mathsf {(4.4)}}\;\sin \left(\beta \right)&={\frac {\overline {AE_{2}}}{\overline {AB}}}={\frac {R\cdot {\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)}{2\cdot R}}={\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)\;=\sin \left(18^{\circ }\right)\\&\Rightarrow \angle \;ABE_{2}=\beta =18^{\circ }\end{aligned}}}$

${\displaystyle {\begin{aligned}{\mathsf {(4.5)}}\;\cos \left(\beta \right)&={\frac {\overline {BE_{2}}}{\overline {AB}}}={\frac {R\cdot {\frac {1}{2}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}}{2\cdot R}}={\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}\;=\cos \left(18^{\circ }\right)\end{aligned}}}$

${\displaystyle {\mathsf {(5)}}}$ Isosceles triangle ${\displaystyle E_{1}E_{2}M}$

${\displaystyle {\mathsf {(5.1)}}\;{\overline {E_{1}E_{2}}}=a}$ (Side length)

${\displaystyle {\mathsf {(5.2)}}\;\angle {HME_{2}}={\frac {1}{2}}\cdot \mu =12^{\circ }}$

${\displaystyle {\mathsf {(5.3)}}\sin \left(18^{\circ }\right)={\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)}$ from (4.4)

${\displaystyle {\mathsf {(5.4)}}\cos \left(18^{\circ }\right)={\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}}$ from (4.5)

To calculate the side length, you need the value of , which can be calculated using the addition theorems : ${\displaystyle \sin(12^{\circ })}$

${\displaystyle {\begin{aligned}{\mathsf {(6)}}\;\sin(12^{\circ })&=\sin(30^{\circ }-18^{\circ })\\&=\sin(30^{\circ })\cdot \cos \left(18^{\circ }\right)-\cos \left(30^{\circ }\right)\cdot \sin \left(18^{\circ }\right)\\&={\frac {1}{2}}\cdot {\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}-{\frac {1}{2}}\cdot {\sqrt {3}}\cdot {\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)\\&={\frac {1}{8}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\end{aligned}}}$

This results in the side length:

${\displaystyle {\begin{aligned}{\mathsf {(7)}}\;a&=2\cdot R\cdot \sin \left(12^{\circ }\right)\\&=2\cdot R\cdot {\frac {1}{8}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\\&={\frac {1}{4}}\cdot R\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\end{aligned}}}$

Calculation of the inscribed radius

The formula for the incircle radius given in the table above is derived as follows: ${\displaystyle r={\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)}$

${\displaystyle {\mathsf {(1)}}}$ Right triangle ${\displaystyle MHE_{2}}$

${\displaystyle {\mathsf {(1.1)}}\;{\overline {MH}}=r=a\cdot {\frac {1}{2}}\cdot \cot \left(12^{\circ }\right)}$from mathematical relationships, incircle radius

${\displaystyle {\mathsf {(1.2)}}\;\angle {HME_{2}}={\frac {1}{2}}\cdot \mu =12^{\circ }}$

${\displaystyle {\mathsf {(1.3)}}\sin \left(12^{\circ }\right)={\frac {1}{8}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)}$from calculation of the side length (6.1)

To calculate the incircle radius you first need the value for the term, which can be calculated using the addition theorems: ${\displaystyle \cot(12^{\circ })={\frac {\cos(12^{\circ })}{\sin(12^{\circ })}}}$ ${\displaystyle \cos(12^{\circ }),}$

${\displaystyle {\begin{aligned}{\mathsf {(2)}}\;\cos(12^{\circ })&=\cos(30^{\circ }-18^{\circ })\\&=\cos(30^{\circ })\cdot \cos \left(18^{\circ }\right)+\sin \left(30^{\circ }\right)\cdot \sin \left(18^{\circ }\right)\\&={\frac {1}{2}}\cdot {\sqrt {3}}\cdot {\frac {1}{4}}\cdot {\sqrt {2\cdot \left(5+{\sqrt {5}}\right)}}+{\frac {1}{2}}\cdot {\frac {1}{4}}\cdot \left({\sqrt {5}}-1\right)\\&={\frac {1}{8}}\cdot \left({\sqrt {3}}\left({\sqrt {10+2\cdot {\sqrt {5}}}}\right)\right)+{\frac {1}{8}}\cdot \left({\sqrt {5}}-1\right)\\&={\frac {1}{8}}\cdot \left({\sqrt {30+6{\sqrt {5}}}}+{\sqrt {5}}-1\right)\end{aligned}}}$

The following derived relationship can be used to transform arithmetic expressions.

${\displaystyle {\begin{aligned}{\mathsf {(3)}}\;{\sqrt {10+2{\sqrt {5}}}}&=({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}\end{aligned}}}$   because it applies

${\displaystyle {\begin{aligned}{\mathsf {(3.1)}}\;({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}&={\sqrt {({\sqrt {5}}-1)^{2}\,(5+2{\sqrt {5}})}}\\&={\sqrt {(5-2{\sqrt {5}}+1)\,(5+2{\sqrt {5}})}}\\&={\sqrt {(6-2{\sqrt {5}})\,(5+2{\sqrt {5}})}}\\&={\sqrt {30+12{\sqrt {5}}-10{\sqrt {5}}-20}}\\&={\sqrt {10+2{\sqrt {5}}}}\end{aligned}}}$

${\displaystyle {\begin{aligned}{\mathsf {(4)}}\;\sin \left(12^{\circ }\right)&={\frac {1}{8}}\,\left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {3}}-{\sqrt {15}}\right)\qquad {\mbox{(aus (1.3))}}\\&={\frac {1}{8}}\,\left(({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}\,({\sqrt {5}}-1)\right)\qquad {\mbox{(nach (3))}}\\&={\frac {1}{8}}\,({\sqrt {5}}-1)\left({\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}\right)\\\end{aligned}}}$

${\displaystyle {\begin{aligned}{\mathsf {(5)}}\;\cos \left(12^{\circ }\right)&={\frac {1}{8}}\,\left({\sqrt {30+6{\sqrt {5}}}}+{\sqrt {5}}-1\right)\qquad {\mbox{(aus (2))}}\\&={\frac {1}{8}}\,\left({\sqrt {3}}\,{\sqrt {10+2{\sqrt {5}}}}+{\sqrt {5}}-1\right)\\&={\frac {1}{8}}\,\left({\sqrt {3}}\,({\sqrt {5}}-1)\,{\sqrt {5+2{\sqrt {5}}}}+({\sqrt {5}}-1)\right)\qquad {\mbox{(nach (3))}}\\&={\frac {1}{8}}\,({\sqrt {5}}-1)\,\left({\sqrt {3}}\,{\sqrt {5+2{\sqrt {5}}}}+1\right)\\\end{aligned}}}$

For the final calculation of the incircle radius, the value of is now determined. ${\displaystyle \cot \left(12^{\circ }\right)}$

${\displaystyle {\begin{aligned}{\mathsf {(6)}}\;\cot \left(12^{\circ }\right)&={\frac {\cos \left(12^{\circ }\right)}{\sin \left(12^{\circ }\right)}}\\&={\frac {{\frac {1}{8}}\,({\sqrt {5}}-1)\,\left({\sqrt {15+6{\sqrt {5}}}}+1\right)}{{\frac {1}{8}}\,({\sqrt {5}}-1)\,\left({\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}\right)}}\\&={\frac {{\sqrt {15+6{\sqrt {5}}}}+1}{{\sqrt {5+2{\sqrt {5}}}}-{\sqrt {3}}}}\\\end{aligned}}}$

• For reasons of a better overview, eight intermediate calculation steps are only visible in edit mode!

${\displaystyle \;{\begin{aligned}\cot \left(12^{\circ }\right)&={\frac {2{\sqrt {15}}+2{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}\,({\sqrt {5}}-1)}{4}}\\&={\frac {{\sqrt {15}}+{\sqrt {3}}+{\sqrt {10+2{\sqrt {5}}}}}{2}}\qquad {\mbox{(nach (3))}}\\&={\frac {1}{2}}\left({\sqrt {10+2{\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\end{aligned}}}$

This results in the inscribed radius ${\displaystyle r}$

${\displaystyle {\begin{aligned}{\mathsf {(7)}}\;r&=a\cdot {\frac {1}{2}}\cdot \cot \left(12^{\circ }\right)\\&=a\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\\&={\frac {1}{4}}\cdot a\cdot \left({\sqrt {10+2\cdot {\sqrt {5}}}}+{\sqrt {15}}+{\sqrt {3}}\right)\\\end{aligned}}}$

Construction with compass and ruler with a given side length

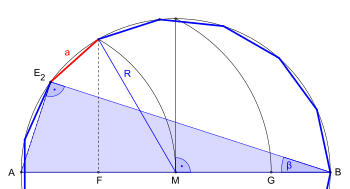
The construction is almost the same as that of the pentagon with a given side length , the representation succeeds by extending the side and a distance generated with it, here the outer division is divided according to the golden ratio . ${\displaystyle {\overline {FE_{2}}}{\text{,}}}$

${\displaystyle {\overline {E_{1}E_{2}}}}$denotes the distance between points and ${\displaystyle E_{1}}$ ${\displaystyle E_{2}{\text{.}}}$

Construction sketch		Animation of the sketch

Given one side of a fifteenagon, a regular fifteenagon can be constructed by:

1. Designate the ends of the route with E ₁ and E ₂ ; both are corner points of the emerging fifteen-square
2. Extend the route E ₁ E ₂ from E ₁ by approximately one length of this route
3. Draw an arc around E ₁ with the radius E ₁ E ₂
4. Construction of a perpendicular to the line E ₁ E ₂ from E ₁ ; The point of intersection with the arc around E ₁ is A.
5. Draw an arc around E ₂ with the radius E ₁ E ₂ ; Points of intersection with arcs around E ₁ are B and C
6. Draw a straight line from C through B (mid-perpendicular of E ₁ E ₂ ) that is a little more than three times as long as BC ; The point of intersection with E ₁ E ₂ is D.
7. Draw an arc around D with radius DA ; The point of intersection with the extension of the line E ₁ E ₂ is F.
8. Draw an arc around E ₂ with a radius E ₂ F ; The point of intersection with the straight line (from C through B) is G
9. Draw a short circular arc around E ₂ with radius CG ; The point of intersection with the extension of the line CB is M, the center point of the circumference of the resulting fifteen-triangle
10. Draw the circle k ₁ around M with the radius ME ₂ ; The point of intersection with the arc around E ₂ is corner point E ₃
11. eleven ablation of the tendon E ₁ E ₂ from k ₁ to k ₁ ; Points of intersection with k ₁ are the corner points E _{3-15 of} the fifteenth corner
12. Connect the corner points found in this way.

Calculation of the perimeter radius

The formula for the circumferential radius given in the table above is derived as follows: ${\displaystyle R=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)}$

${\displaystyle {\mathsf {(1)}}\;{\overline {E_{1}E_{2}}}={\overline {E_{1}A}}={\overline {CE_{2}}}=a}$ (Side length)

${\displaystyle {\mathsf {(2)}}\;{\overline {DE_{1}}}={\overline {DE_{2}}}={\frac {1}{2}}\cdot a}$

${\displaystyle {\mathsf {(3)}}}$ Right triangle ${\displaystyle AE_{1}D}$

According to the Pythagorean theorem: ${\displaystyle {\overline {DA}}^{2}={\overline {E_{1}A}}^{2}+{\overline {DE_{1}}}^{2}}$

${\displaystyle {\mathsf {(3.1)}}\;{\overline {DA}}={\sqrt {{{\overline {E_{1}A}}^{2}}+{{\overline {DE_{1}}}^{2}}}}={\sqrt {a^{2}+\left({\frac {1}{2}}\right)^{2}\cdot a^{2}}}=a\cdot {\sqrt {1+{\frac {1}{4}}}}=a\cdot {\frac {\sqrt {5}}{2}}}$

${\displaystyle {\mathsf {(3.2)}}\;{\overline {DF}}={\overline {DA}}=a\cdot {\frac {\sqrt {5}}{2}}}$ after construction, step 7

${\displaystyle {\mathsf {(4)}}\;{\overline {E_{1}F}}={\overline {DF}}-{\overline {DE_{1}}}=a\cdot {\frac {\sqrt {5}}{2}}-a\cdot {\frac {1}{2}}=a\cdot \left({\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\right)=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)}$

${\displaystyle {\begin{aligned}{\mathsf {(5)}}\;{\overline {E_{2}F}}&=a+{\overline {E_{1}F}}=a+a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)=a\cdot \left(1+{\frac {1}{2}}\cdot \left({\sqrt {5}}-1\right)\right)\\&=a\cdot \left(1+{\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\right)=a\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)\end{aligned}}}$

${\displaystyle {\mathsf {(5.1)}}\;{\overline {E_{2}G}}={\overline {E_{2}F}}=a\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)}$ after construction, step 8

${\displaystyle {\mathsf {(6)}}}$ Right triangle ${\displaystyle DE_{2}G}$

According to the Pythagorean theorem: ${\displaystyle {\overline {E_{2}G}}^{2}={\overline {DE_{2}}}^{2}+{\overline {DG}}^{2}}$

${\displaystyle {\begin{aligned}(6.1)\;{\overline {DG}}\;&={\sqrt {{{\overline {E_{2}G}}^{2}}-{{\overline {DE_{2}}}^{2}}}}={\sqrt {a^{2}\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)^{2}-a^{2}\cdot \left({\frac {1}{2}}\right)^{2}}}=a\cdot {\sqrt {\left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)^{2}-\left({\frac {1}{2}}\right)^{2}}}\\&=a\cdot {\sqrt {{\frac {1}{4}}+{\frac {\sqrt {5}}{2}}+{\frac {5}{4}}-{\frac {1}{4}}}}=a\cdot {\sqrt {{\frac {5}{4}}+{\frac {2\cdot {\sqrt {5}}}{4}}}}=a\cdot {\sqrt {{\frac {1}{4}}\cdot \left(5+2\cdot {\sqrt {5}}\right)}}=a\cdot {\frac {1}{2}}\cdot {\sqrt {5+2\cdot {\sqrt {5}}}}\end{aligned}}}$

${\displaystyle {\mathsf {(7)}}}$ Right triangle ${\displaystyle {DCE_{2}}}$

According to the Pythagorean theorem: ${\displaystyle {\overline {CE_{2}}}^{2}={\overline {DE_{2}}}^{2}+{\overline {DC}}^{2}}$

${\displaystyle (7.1)\;{\overline {DC}}={\sqrt {{\overline {CE_{2}}}^{2}-{\overline {DE_{2}}}^{2}}}={\sqrt {a^{2}-a^{2}\cdot \left({\frac {1}{2}}\right)^{2}}}=a\cdot {\sqrt {\left(1-{\frac {1}{4}}\right)}}=a\cdot {\sqrt {\frac {3}{4}}}=a\cdot {\frac {\sqrt {3}}{2}}}$

After construction, step 9 applies to the perimeter radius ${\displaystyle R:}$

${\displaystyle {\begin{aligned}(8)\;R&={\overline {E_{2}M}}={\overline {CG}}\\&={\overline {DG}}+{\overline {DC}}=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}\right)+a\cdot {\frac {\sqrt {3}}{2}}\\&=a\cdot {\frac {1}{2}}\cdot \left({\sqrt {5+2\cdot {\sqrt {5}}}}+{\sqrt {3}}\right)\approx 2{,}405\cdot a\end{aligned}}}$

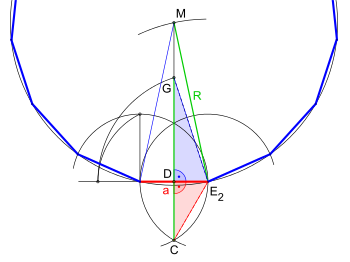
The golden ratio in the fifteenth corner

The golden ratio is used to determine construction elements both in the construction with a given circumference and in the given side length .

Part of the construction sketch for a given perimeter		Part of the construction sketch for a given side length

• In the construction for a given circumference, the point divides the distance in the ratio of the golden section: ${\displaystyle M}$ ${\displaystyle {\overline {AG}}}$

${\displaystyle {\frac {\overline {AM}}{\overline {MG}}}={\frac {\overline {AG}}{\overline {AM}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1{,}618{\text{.}}}$

• In the construction for a given side length, the side is lengthened so that it is the longer distance of the ratio:

${\displaystyle {\frac {\overline {E_{1}E_{2}}}{\overline {E_{1}F}}}={\frac {\overline {E_{2}F}}{\overline {E_{1}E_{2}}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1{,}618{\text{.}}}$

See also

• Tendon polygon
• Regular polygon

literature

• H. Maser: Die Teilung des Kreises ..., Article 365. , in Carl Friedrich Gauss' studies on higher arithmetic , published by Julius Springer, Berlin 1889; Göttingen Digitization Center, University of Göttingen; accessed on March 15, 2018.

Web links

• Eric W. Weisstein : Pentadecagon . In: MathWorld (English). Retrieved October 4, 2015.

Individual evidence

1. ↑ Jürgen Köller: Regular polygon. In: Mathematical handicrafts. 2005, accessed October 4, 2015 . 
2. ^ Johann Karl Friedrich Hauff: EUKLIDS ELEMENTS. THE FIRST TO THE SIXTH, TOGETHER THE EIGHTH AND TWELFTH BEECH . Neue Academische Buchhandlung, Marburg 1807, p. 129 f . ( limited preview in Google Book search).
3. ↑ Johannes Kepler: WORLD HARMONICS. XLIV. Set., Page of the fifteen-sided, page 44, regenerated from the Internet Archive . In: Google Books. R. OLDENBURG VERLAG 2006, translated and introduced by MAX CASPAR 1939, p. 401 , accessed on July 19, 2019 .