VSEPR model
The VSEPR model (abbreviation for English valence shell electron pair repulsion , German valence shell electron pair repulsion ), also EPA model (electron pair repulsion model) or originally VEPR theory (English valence electron pair repulsion theory ), leads the spatial shape of a Molecule back to the repulsive forces between the electron pairs of the valence shell .
The model is also called Gillespie - Nyholm theory after its developers .
The derived rules
The following rules for molecules of the type AX n result from the VSEPR model :
- The electron pairs of the valence shell of the central atom (A), i.e. H. of the atom in the center of the molecule, arrange themselves in such a way that the distance between them is as large as possible.
- The free electron pairs (symbolized here with E) in a molecule of the type AX n E m take up more space than the binding electron pairs and thus lead to an increase in the angle XAE and a decrease in the angle XAX.
- Individual free electrons in radicals take up less space than free electron pairs .
- Larger electronegativity differences between A and X thus reduce the space requirement of the corresponding binding .
- Multiple bonds take up more space than single bonds , with the space required increasing with the order of the bond .
- However, only the sigma bonds are used to determine the coarse molecular structure . H. Multiple bonds are treated like single bonds here.
- Smaller central atoms or larger negatively polarized ligands cause a strong steric and electronic repulsion force that can exceed that of a lone pair of electrons.
Predictions for free electron pairs on the central atom
If there are no lone pairs of electrons on the central atom, molecular structures can be predicted quite simply by counting the “ residues ”.
Nevertheless, the consideration of compounds with one or more stereochemically active, lone pairs of electrons can also be approximated. To do this, they are treated as pseudo-ligands - similar to binding partners - and marked with the Greek letter “ψ”. This is how you get to the pseudo structure of the respective molecule.
Example: the oxygen atom of the water molecule , to which two hydrogen atoms are covalently bound (X = 2), has two free electron pairs (E = 2). This results in a number of # = 2 + 2 = 4 pseudo-ligand, and thus a pseudo-tetrahedral structure (structure type) as ψ 2 - tetrahedron can be described. By “thinking away” the free electron pairs, what remains is the real structure (molecular structure), which is angled in this case and which is only described by the atomic nuclei.
An example of a ψ 1 tetrahedron, i. H. with only one lone pair of electrons, the ammonia molecule is NH 3 .
| # | Molecular types a | example | Ψ - structure / pseudo structure b | Real structure c | Angle d |
|---|---|---|---|---|---|
| 1 |
AX 1 |
H 2 |
linear |
linear |
|
| 2 |
AX 2 |
BeCl 2 CO 2 |
linear |
linear |
180 ° |
|
AX 1 E 1 |
CO |
linear |
linear |
||
| 3 |
AX 3 |
BF 3 NO 3 - CO 3 2− |
trigonal planar |
 trigonal planar |
120 ° |
 AX 2 E |
SO 2 O 3 NO 2 - |
 trigonal planar |
angled |
approx. 115 ° | |
|
AX 1 E 2 |
trigonal planar |
linear |
|||
| 4th |
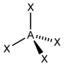 AX 4 |
CH 4 SO 4 2− PO 4 3− ClO 4 - |
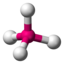 tetrahedral |
 tetrahedral |
109.5 ° |
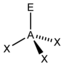 AX 3 E |
NH 3 PCl 3 |
 tetrahedral |
 trigonal - pyramidal |
approx. 107 ° | |
 AX 2 E 2 |
H 2 O |
 tetrahedral |
angled |
approx. 104 ° | |
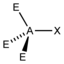 AX 1 E 3 |
HCl |
 tetrahedral |
linear |
||
| 5 |
 AX 5 |
PCl 5 |
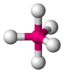 trigonal - bipyramidal |
 trigonal-bipyramidal |
120 ° / 90 ° |
 AX 4 E |
SF 4 , SCl 4 |
 trigonal-bipyramidal |
"Seesaw", bisphenoidal |
approx. 175 ° / 110 ° | |
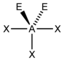 AX 3 E 2 |
ClF 3 |
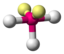 trigonal-bipyramidal |
T-shaped |
approx. 87.5 ° | |
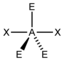 AX 2 E 3 |
XeF 2 |
trigonal-bipyramidal |
linear |
180 ° | |
| 6th |
 AX 6 |
SF 6 |
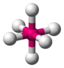 octahedral (= square-bipyramidal, trigonal-antiprismatic) |
 octahedral (= square-bipyramidal, trigonal-antiprismatic) |
90 ° |
 AX 5 E |
ClF 5 |
 octahedral (= square-bipyramidal, trigonal-antiprismatic) |
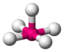 square-pyramidal |
approx. 85 ° | |
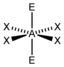 AX 4 E 2 |
XeF 4 |
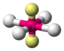 octahedral (= square-bipyramidal, trigonal-antiprismatic) |
square-planar |
90 ° | |
| 7th |
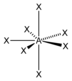 AX 7 |
IF 7 |
 pentagonal - bipyramidal |
 pentagonal-bipyramidal |
90 ° / 72 ° |
 AX 6 E |
[XeOF 5 ] - |
 pentagonal-bipyramidal |
pentagonal-pyramidal |
approx. 90 ° / approx. 72 ° | |
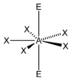 AX 5 E 2 |
XeF 5 - |
pentagonal-bipyramidal |
pentagonal planar |
72 ° | |
| 8th | AX 8 | IF 8 - |

|

tetragonal-antiprismatic |
78 ° / 73 ° |
Remarks:
Limits of applicability
The VSEPR model can be applied to molecules in which the residues bound to the central atom (atoms or groups of atoms) do not become too large and do not have any specific interactions with one another.
It cannot be used or only to a limited extent for transition metal compounds. In many cases, however, the bond angles do not agree with the model even with simple molecules. For compounds with delocalized electrons , the application of the model can also be associated with difficulties; here it is necessary to consult the molecular orbital theory .
literature
- Reinhart Ahlrichs: Gillespie and Pauling models - a comparison . In: Chemistry in Our Time . tape 14 , no. 1 , 1980, p. 18–24 , doi : 10.1002 / ciuz.19800140104 .
- Ronald J. Gillespie, Edward A. Robinson: Models of molecular geometry . In: Chemical Society Reviews . tape 34 , no. 5 , 2005, p. 396-407 , doi : 10.1039 / B405359C .
- RJ Gillespie, I. Hargittai: The VSEPR Model of Molecular Geometry. 8th ed., Allyn & Bacon, Boston 1991, ISBN 978-0-205-12369-8 .
Web links
Individual evidence
- ^ AF Holleman , E. Wiberg , N. Wiberg : Textbook of Inorganic Chemistry . 101st edition. Walter de Gruyter, Berlin 1995, ISBN 3-11-012641-9 , p. 136.

