Triangle

Regular triangle

The Dreizehneck or Tridekagon is a geometric figure , and a polygon ( polygon ). It is determined by thirteen points and their thirteen connections, called lines , sides or edges.

Variations

The triangle can be represented as:

• concave triangle in which at least one interior angle is greater than 180 °. A triangle can have a maximum of six such angles.
• convex triangle in which all interior angles are less than 180 °. A convex triangle can be regular or irregular.
• Tendon triangle in which all corners lie on a common circumference , but the side lengths are unequal.
• regular triangle: it is determined by thirteen points on a virtual circle. The adjacent points to each other have always the same distance and are connected by juxtaposed tracks , even sides or edges , called connected.
• Regular crossed triangle: This results when at least one is skipped over each time when connecting the thirteen corner points and the chords thus created are of the same length. Such regular stars are noted with Schläfli symbols , indicating the number of corner points and connecting every -th point. ${\displaystyle \left\{n/k\right\}}$ ${\displaystyle n}$ ${\displaystyle k}$

The following gallery shows the five possible regular thirteen-ray stars, also known as tridecagrams.

• Regular thirteen-ray stars
• 

  ${\displaystyle \left\{13/2\right\}{,}\ \left\{13/11\right\}}$

• 

  ${\displaystyle \left\{13/3\right\}{,}\ \left\{13/10\right\}}$

• 

  ${\displaystyle \left\{13/4\right\}{,}\ \left\{13/9\right\}}$

• 

  ${\displaystyle \left\{13/5\right\}{,}\ \left\{13/8\right\}}$

• 

  ${\displaystyle \left\{13/6\right\}{,}\ \left\{13/7\right\}}$

Regular triangle

According to Carl Friedrich Gauß and Pierre-Laurent Wantzel, the regular three -octagon is not a constructible polygon , because its number of sides is not a product of a power of two with pairwise different Fermat's prime numbers . ${\displaystyle n=13}$

Sizes

Sizes of a regular triangle
Interior angle	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {11}{13}}\cdot 180^{\circ }\\\alpha &=152{,}{\overline {307692}}^{\circ }\end{aligned}}}$
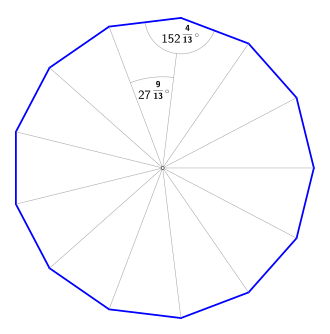
Central angle (Center angle)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{13}}\\\mu &=27{,}{\overline {692307}}^{\circ }\end{aligned}}}$
Side length	${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\\a&\approx 0{,}478631\cdot R\end{aligned}}}$
Perimeter radius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)}}\\R&\approx {\frac {a}{0{,}478631}}\end{aligned}}}$
Inscribed radius	${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\\r&\approx 0{,}970941\cdot R\end{aligned}}}$
height	${\displaystyle {\begin{aligned}h&=R+r=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{13}}\right)\right)\\h&\approx 1{,}9709418\cdot R\end{aligned}}}$
Area	${\displaystyle {\begin{aligned}A&=13\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\\A&\approx 3{,}0207006\cdot R^{2}\end{aligned}}}$

Mathematical relationships

Interior angle

The interior angle is enclosed by two adjacent side edges. In the general formula for regular polygons, the variable stands for the number of corner points of the polygon. In this case, the number should be used for the variable . ${\displaystyle \alpha }$ ${\displaystyle n}$ ${\displaystyle 13}$

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {13-2}{13}}\cdot 180^{\circ }={\frac {11}{13}}\cdot 180^{\circ }=152{,}{\overline {307692}}^{\circ }}$

Central angle

The central angle or center angle is enclosed by two adjacent circumferential radii . Enter the number for the variable in the general formula . ${\displaystyle \mu }$ ${\displaystyle R}$ ${\displaystyle n}$ ${\displaystyle 13}$

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{13}}=27{,}{\overline {692307}}^{\circ }}$

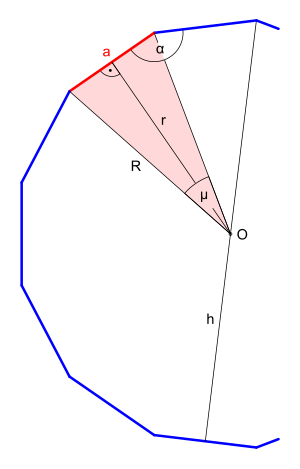
Side length and perimeter radius

The triangle is divisible into thirteen isosceles triangles , so-called partial triangles . From half of such a partial triangle, i.e. from a right-angled triangle with the cathetus (half the side length) , the hypotenuse (circumferential radius) and the half central angle , the side length is obtained with the help of trigonometry in the right triangle as follows ${\displaystyle {\frac {a}{2}}}$ ${\displaystyle R}$ ${\displaystyle {\frac {\mu }{2}}}$ ${\displaystyle a}$

${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {\mu }{2}}\right)=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\\&=R\cdot 2\cdot \sin \left(13{,}{\overline {846153}}^{\circ }\right)\\a&\approx 0{,}478631\cdot R,\end{aligned}}}$

the circumferential radius is obtained by forming ${\displaystyle R}$

${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)}}\\R&\approx {\frac {a}{0{,}478631}}\end{aligned}}}$

Inscribed radius

The incircle radius is the height of a partial triangle, perpendicular to the side of the triangle . If the same right-angled triangle is used again for the calculation as for the side length, the inscribed radius applies ${\displaystyle r}$ ${\displaystyle a}$ ${\displaystyle r}$

${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {\mu }{2}}\right)=R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\\r&\approx 0{,}970941\cdot R\end{aligned}}}$

height

The height of a regular triangle results from the sum of the incircle radius and the circumferential radius. ${\displaystyle h}$

${\displaystyle h=R+r=R+R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{13}}\right)\right)}$

${\displaystyle h\approx 1{,}970941817\cdot R}$

Area

The area of ​​a triangle is generally calculated . For the calculation of the triangle, the results of the side length and the incircle radius are used, which is used for the height . ${\displaystyle A_{\Delta }={\frac {1}{2}}a\cdot h_{a}}$ ${\displaystyle a}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle h_{a}}$

${\displaystyle a=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)}$

${\displaystyle h_{a}=r=R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\;}$ from this follows for the area of ​​a partial triangle

${\displaystyle {\begin{aligned}A_{\Delta }&={\frac {1}{2}}\cdot R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot R\cdot \cos \left({\frac {180^{\circ }}{13}}\right)\end{aligned}}\;}$ summarized it results

${\displaystyle A_{\Delta }=R^{2}\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot \cos \left({\frac {180^{\circ }}{13}}\right)}$

${\displaystyle A_{\Delta }\approx 0{,}232361586\cdot R^{2}}$

and for the area of ​​the entire triangle

${\displaystyle A=13\cdot A_{\Delta }=13\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{13}}\right)\cdot \cos \left({\frac {180^{\circ }}{13}}\right)}$

${\displaystyle A\approx 3{,}020700618\cdot R^{2}}$

Geometric constructions

As explained under the regular triangle , a construction with compass and ruler does not provide a solution. However, if additional aids, such as B. the method of Archimedes , Bieberbach's right-angled hook and the tomahawk for a three-way division of the angle or the curves Quadratrix of Hippias and Archimedes' spiral to divide the 90-degree angle into equal angles, an exact construction is feasible. ${\displaystyle n}$

Tomahawk as an additional tool

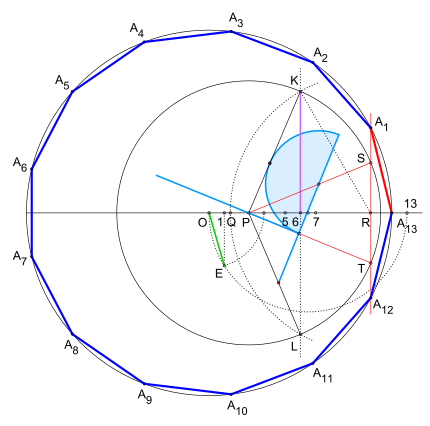
Andrew M. Gleason published two elegant constructions of the regular polygons heptagon and triangle in the mathematical journal The American Mathematical Monthly in 1988 . Both require the angle to be divided into three for an exact solution. Andrew M. Gleason left the method for this open. The following construction sketch (left picture of the double picture) differs from the original in the continuation of the construction up to the finished triangle. The dotted lines are used for clarification, e.g. B. how to create certain function points. More on this in the following description based on the original description.

Trident, construction sketch with tomahawk (light blue)		Animation of the construction sketch

For the triangle one begins in the coordinate origin of a Cartesian coordinate system with a circle around a point with a radius . The point is then determined . To get the point , the numerical values ​​are first determined as the twelfth part of , and the distance is halved and the Thales circle is drawn around its center . The then erected upright on from cuts the Thales circle . The connection of the point with results in the entry of the point . Following the numerical values and to determine as well as the points and draw. ${\displaystyle O(0,0)}$ ${\displaystyle 12}$ ${\displaystyle A_{13}(12,0)}$ ${\displaystyle P\left({\sqrt {13}}-1,0\right)}$ ${\displaystyle 1}$ ${\displaystyle {\overline {O13}}}$ ${\displaystyle 13}$ ${\displaystyle {\overline {O13}}}$ ${\displaystyle {\overline {O13}}}$ ${\displaystyle 1}$ ${\displaystyle E}$ ${\displaystyle O}$ ${\displaystyle E}$ ${\displaystyle {\sqrt {13}}}$ ${\displaystyle P\left({\sqrt {13}}-1,0\right)}$ ${\displaystyle 5}$ ${\displaystyle 7}$ ${\displaystyle {\overline {O13}}}$ ${\displaystyle Q\left(5-{\sqrt {13}},0\right)}$ ${\displaystyle R\left(7+{\sqrt {13}},0\right)}$

To find the points and first the numerical value is set and a vertical line is built through it. If we now draw an arc to by , it intersects the vertical line in and . After connecting the points and with and drawing a circle through , the angle is divided into thirds using a freely selectable method. Here z. B. this is done with the help of a so-called tomahawk , resulting in the points and . A straight line through and results in and , which are the vertices of a regular three-sided triangle . The other corner points can be found one after the other by using the circular arc . ${\displaystyle K}$ ${\displaystyle L}$ ${\displaystyle 6}$ ${\displaystyle {\overline {O13}}}$ ${\displaystyle 6}$ ${\displaystyle R}$ ${\displaystyle Q}$ ${\displaystyle K\left(6,{\sqrt {3}}\cdot \left({\sqrt {13}}+1\right)\right)}$ ${\displaystyle L\left(6,-{\sqrt {3}}\cdot \left({\sqrt {13}}+1\right)\right)}$ ${\displaystyle K}$ ${\displaystyle L}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle K}$ ${\displaystyle LPK}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle A_{1}}$ ${\displaystyle A_{12}}$ ${\displaystyle A_{1},\dots ,A_{13}}$ ${\displaystyle OA_{13}A_{1}}$

Quadratrix des Hippias as an additional aid

Image 1: Regular triangle with a given circumference as an exact construction with the quadrix of Hippias as an additional aid

The construction (Fig. 1) of the triangle with the given circumference is almost identical to that of the elf . For this reason, the description of the elf was adopted with the necessary adjustments.

After the sign of the square , e.g. B. with the side length , and the radius around the point by carried out the construction of the particular curve, the so-called quadratrix of hippias , with the parametric representation : ${\displaystyle 1}$ ${\displaystyle O}$ ${\displaystyle A_{1}}$ ${\displaystyle \gamma \colon (0,{\tfrac {\pi }{2}})\rightarrow \mathbb {R} ^{2}}$

${\displaystyle \gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}}$

With

${\displaystyle {\begin{aligned}x(t)&={\begin{cases}t\cot \left({\frac {\pi t}{2\cdot 1}}\right)\,&,0\leq t\leq 1\end{cases}}\\y(t)&=t\end{aligned}}}$

Then the route is divided into thirteen equally long sections using the route division. For the sake of clarity, only the relevant points are shown in the drawing. ${\displaystyle {\overline {CO}}}$

The central angle of the triangle results from but the quadratrix of Hippias only divides the angles down to the same size. It follows that a thirteenth of the distance can only achieve a thirteenth of the angle . Therefore, because of the calculation of the central angle from the circumference with its four times a thirteenth, i.e. H. the dividing point of the line used to construct the central angle . This arises after the construction of a parallel to from to the curve of the quadratrix, which results in the point . Now you draw a half line from the angle point through to the perimeter. This results in the second corner point on the perimeter . The length of the line is the exact length of the side of the regular triangle. ${\displaystyle \mu ={\frac {360^{\circ }}{13}},}$ ${\displaystyle >0^{\circ }}$ ${\displaystyle \leq 90^{\circ }}$ ${\displaystyle {\overline {CO}}}$ ${\displaystyle 90^{\circ }}$ ${\displaystyle \mu }$ ${\displaystyle 360^{\circ },}$ ${\displaystyle 4'}$ ${\displaystyle {\overline {CO}},}$ ${\displaystyle \mu }$ ${\displaystyle {\overline {A_{1}O}}}$ ${\displaystyle 4'}$ ${\displaystyle D}$ ${\displaystyle O}$ ${\displaystyle D}$ ${\displaystyle A_{2}}$ ${\displaystyle {\overline {A_{1}A_{2}}}}$ ${\displaystyle a}$

After removing the side length eleven times counterclockwise on the circumference and then connecting the neighboring corner points, the triangle is completed. ${\displaystyle a}$ ${\displaystyle A_{1}\ldots A_{13}}$

For a given side length

Image 2: Regular triangle with a given side length (green). Continuation of an exact construction (using the Quadratrix) or an approximate construction. ${\displaystyle a}$

The construction of the triangle with a given side length (see Figure 2) is almost the same as that of the elephant. For this reason, the description of the elf was adopted with the necessary adjustments.

If the side length of a triangle with a given circumference has already been determined - exactly with the help of the quadratrix or approximately -, a triangle with a given side length can be constructed from it using the so-called centric stretching . ${\displaystyle a'}$ ${\displaystyle a}$

Only if the specified side length is longer than , both angle legs of the central angle are first extended. Next, the bisector of the angle is drawn and then the point with any position is determined. There follows a parallel to through . When pulling the semicircle around with radius , the intersection points and result . The two parallels to from and up to the angle legs in question provide the first two corner points and the triangle you are looking for. Finally, the radius found is drawn around with the radius , from the corner point the side length is plotted eleven times counterclockwise on the circumference and the neighboring corner points are connected to one another. ${\displaystyle a}$ ${\displaystyle a'}$ ${\displaystyle \mu }$ ${\displaystyle wh}$ ${\displaystyle \mu }$ ${\displaystyle M}$ ${\displaystyle a'={\overline {A_{1}'A_{2}'}}}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle r={\frac {a}{2}}}$ ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle wh}$ ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle A_{1}}$ ${\displaystyle A_{2}}$ ${\displaystyle r_{u}={\overline {OA_{1}}}}$ ${\displaystyle O}$ ${\displaystyle A_{2}}$ ${\displaystyle a}$

Approximate constructions

There are only a few approximate constructions of the three-octagon described in the relevant literature.

By Albrecht Dürer

Image 3: An elf and on the right the regular triangle according to Dürer (1525) with the empirically determined point near the point ${\displaystyle c}$ ${\displaystyle b}$

In 1525 Albrecht Dürer published in his work Underweysung the measurement, with the Zirckel and Richtscheyt, in lines, planes and wholly in the second book an elagon and a three-octagon (in picture 3 right). The regular triangle inscribed in a circle only needs half the radius and the point near the point to determine the side length . The point , which Dürer did not explain in detail, is determined (empirically) with the help of experiments. ${\displaystyle c}$ ${\displaystyle b}$ ${\displaystyle c}$

“... Weyter was so agile .13. corner should do / so tear jch out of a center .a. a zirckellini After that I tear a half [63] diameter .ab and cut the one with a punched .d. in the with each other and need the leng .cd zue .13. painting around in circles / is also mechanice and nit demonstratiue. "

In his description, Dürer particularly points out that this is an approximate (“mechanical”) and not an exact (“demonstrative”) construction. The absolute error of the first side length constructed in this way depends on the accuracy of the empirically determined point . ${\displaystyle c}$

With a universal method

Fig. 4: Trident, approximation construction with a universal method

Figure 4 shows a triangle in its circumference, created with a universal method.

First, the distance , later the diameter of the triangle you are looking for, is divided into parts of equal length with the aid of the theorem of rays (not shown in the drawing) or determined by stringing together equally long distances. Now either the even or the odd numbers (division points) are marked. In this example the even numbers and are entered. The subsequent halving of is done with the help of the two arcs around or with the radius . The arcs intersect at the points and by connecting them you get the center point and the axis of symmetry. ${\displaystyle {\overline {AB}}}$ ${\displaystyle 13}$ ${\displaystyle 13}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle 2,4,6,8,10}$ ${\displaystyle 12}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle C}$ ${\displaystyle D.}$ ${\displaystyle O}$

After drawing in the radius around by it continues with setting the key points on the perimeter. The ruler is placed on the point and on the even number . Then draw a short line along the ruler through the opposite half of the circumferential line, results in the corner point of the resulting three-sided triangle . This procedure is repeated when determining the corner points. It is continued, starting from the point until the remaining corner points are found. Finally, the neighboring corner points are connected to one another. ${\displaystyle O}$ ${\displaystyle A}$ ${\displaystyle D}$ ${\displaystyle 2}$ ${\displaystyle E_{6}}$ ${\displaystyle E_{5}\ldots E_{1}.}$ ${\displaystyle C,}$ ${\displaystyle E_{8}\ldots E_{13}}$

The special thing about this method is that six sides of the triangle have the same length in pairs, e.g. B. the sides and the side has a different length from the others. ${\displaystyle {\overline {E_{6}E_{7}}}}$ ${\displaystyle {\overline {E_{7}E_{8}}}.}$ ${\displaystyle {\overline {E_{1}E_{13}}}}$

Largest and smallest absolute error of the side lengths for a circumferential radius with : ${\displaystyle R=1\;\mathrm {m} }$

${\displaystyle {\overline {E_{1}E_{13}}}\approx 21{,}26\;\mathrm {mm} }$

${\displaystyle {\overline {E_{4}E_{5}}}}$ and ${\displaystyle {\overline {E_{9}E_{10}}}\approx -1{,}176704\;\mathrm {mm} }$

${\displaystyle {\overline {E_{3}E_{4}}}}$ and ${\displaystyle {\overline {E_{10}E_{11}}}\approx 1{,}193636\;\mathrm {mm} }$

If you look at the two smallest absolute errors of the neighboring sides, it follows that both are almost equally distant from an ideal center . That means, if one would use this approximation construction z. B. only construct the lines and , then constructively determine the arithmetic mean of these lines, this would result in a side length of the triangle with a deviation of ${\displaystyle 0\;mm}$ ${\displaystyle {\overline {E_{9}E_{10}}}}$ ${\displaystyle {\overline {E_{10}E_{11}}}}$

${\displaystyle {\frac {1}{2}}\cdot \left(-1{,}176704\ldots \,\mathrm {mm} +1{,}193636\ldots \,\mathrm {mm} \right)=0{,}008466\ldots \;\mathrm {mm} }$.

Or to put it another way, with a circumcircle radius the deviation would be the constructed first side . ${\displaystyle R=1\;\mathrm {km} }$ ${\displaystyle \approx 8{,}5\;\mathrm {mm} }$

Occurrence

• Examples of coins with the shape or embossed figure of a regular triangle:

• 

  Czech 20-krone coin ,
  with rounded edges (1997)
  on the left front with the Bohemian Lion ,
  on the right back with the Wenceslas statue on Wenceslas Square .

• 

  Tunisian 200 millim coin (2013),
  with rounded edges,
  reverse side on the left, obverse on the right.

• 

  Tunisian 2-dinar coin (2013),
  with rounded edges,
  left reverse with the port of Carthage , right obverse with an olive tree .

literature

• H. Maser: Die Teilung des Kreises ..., Article 365. , in Carl Friedrich Gauss' studies on higher arithmetic , published by Julius Springer, Berlin 1889; Göttingen Digitization Center, University of Göttingen; accessed on March 15, 2018.

Web links

Wiktionary: Dreizehneck  - explanations of meanings, word origins, synonyms, translations

• Trident, variant of the approximate construction with a universal method
• Trident with a given side length , exact construction ${\displaystyle a}$

Individual evidence

1. ↑ Andrew Gleason : Angle Trisection, the Heptagon, and the Triskaidecagon . In: The American Mathematical Monthly . tape 95 , no. 3 , 1988, pp. 185–194 , JSTOR : 2323624 ( math.fau.edu, Fig. 4. Construction of a regular triskaidecagon., Page 193 ff., PDF accessed on May 15, 2019).
2. ↑ Hans-Wolfgang Henn: Elementary Geometry and Algebra . Verlag Vieweg + Teubner 2003, pp. 45–48 Die Quadratur des Kreises ( excerpt (Google) ), accessed on October 29, 2017
3. ↑ Horst Hischer: Mathematik in der Schule 32 (1994) 5, History of Mathematics as a Didactic Aspect (2). Solution of classic problems. (PDF) p. From 279 , accessed on October 29, 2017 . 
4. ↑ Albrecht Dürer: Underweysung the measurement, with the Zirckel and Richtscheyt, in lines, planes and whole corporen . Nuremberg 1525 ( ETH library, construction of a regular eleven and three-sided triangle, p. 63, Fig. 19 [accessed on October 17, 2017]).
5. ^ H. August: Drawing construction of an elf. In: Drawing constructions: polygons. Retrieved October 17, 2017 . 
6. ^ Peter Eckardt: Siebeneck. In: Stars and Polygons. Retrieved October 17, 2017 .