51-corner

Regular 51-sided

The 51-Eck or Pentakontahenagon is a geometric figure , and a polygon ( polygon ). It is determined by fifty-one points and their fifty-one connections called lines , sides or edges.

Regular 51-sided

According to Carl Friedrich Gauß and Pierre-Laurent Wantzel, the regular 51-gon is a constructible polygon , since the number of its sides can be represented as the product of a power of two with pairwise different Fermat's prime numbers ( ). ${\displaystyle 51=2^{0}\cdot 3\cdot 17}$

Sizes

Sizes of a regular 51-sided
Interior angle	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {49}{51}}\cdot 180^{\circ }\\\alpha &\approx 172{,}941176^{\circ }\end{aligned}}}$
Central angle (Center angle)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{51}}\\\mu &\approx 7{,}058823^{\circ }\end{aligned}}}$
Side length	${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{51}}\right)\\a&\approx 0{,}1231218\cdot R\end{aligned}}}$
Perimeter radius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{51}}\right)}}\\R&\approx {\frac {a}{0{,}123121}}\end{aligned}}}$
Inscribed radius	${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {180^{\circ }}{51}}\right)\\r&\approx 0{,}998103\cdot R\end{aligned}}}$
height	${\displaystyle {\begin{aligned}h&=R+r=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{51}}\right)\right)\\h&\approx 1{,}998103\cdot R\end{aligned}}}$
Area	${\displaystyle {\begin{aligned}A&=51\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{51}}\right)\cdot \cos \left({\frac {180^{\circ }}{51}}\right)\\A&\approx 3{,}133651\cdot R^{2}\end{aligned}}}$

Mathematical relationships

Interior angle

The interior angle is enclosed by two adjacent side edges. In the general formula for regular polygons, the variable stands for the number of corner points of the polygon. In this case, the number should be used for the variable . ${\displaystyle \alpha }$ ${\displaystyle n}$ ${\displaystyle 51}$

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {51-2}{51}}\cdot 180^{\circ }={\frac {49}{51}}\cdot 180^{\circ }\approx 172{,}941176^{\circ }}$

Central angle

The central angle or center angle is enclosed by two adjacent circumferential radii . Enter the number for the variable in the general formula . ${\displaystyle \mu }$ ${\displaystyle R}$ ${\displaystyle n}$ ${\displaystyle 51}$

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{51}}\approx 7{,}058823^{\circ }}$

Side length and perimeter radius

The 51-gon can be divided into fifty-one isosceles triangles, so-called sub - triangles . From half of such a partial triangle, i.e. from a right-angled triangle with the cathetus (half the side length) , the hypotenuse (circumferential radius) and the half central angle , the side length is obtained with the help of trigonometry in the right triangle as follows ${\displaystyle {\frac {a}{2}}}$ ${\displaystyle R}$ ${\displaystyle {\frac {\mu }{2}}}$ ${\displaystyle a}$

${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {\mu }{2}}\right)\\&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{51}}\right)\\a&\approx 0{,}1231218\cdot R,\end{aligned}}}$

the circumferential radius is obtained by forming ${\displaystyle R}$

${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{51}}\right)}}\\R&\approx {\frac {a}{0{,}1231218}}\end{aligned}}}$

Inscribed radius

The incircle radius is the height of a partial triangle, perpendicular to the side length of the 51 corner. If the same right-angled triangle is used again for the calculation as for the side length, the inscribed radius applies ${\displaystyle r}$ ${\displaystyle a}$ ${\displaystyle r}$

${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {\mu }{2}}\right)=R\cdot \cos \left({\frac {180^{\circ }}{51}}\right)\\r&\approx 0{,}998103\cdot R\end{aligned}}}$

height

The height of a regular 51-sided results from the sum of the incircle radius and the circumferential radius . ${\displaystyle h}$ ${\displaystyle r}$ ${\displaystyle R}$

${\displaystyle h=R+r=R+R\cdot \cos \left({\frac {180^{\circ }}{51}}\right)=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{51}}\right)\right)}$

${\displaystyle h\approx 1{,}998103\cdot R}$

Area

The area of ​​a triangle is generally calculated . For the calculation of the 51-gon the results of the side length and the incircle radius are used, which is used for the height . ${\displaystyle A_{\Delta }={\frac {1}{2}}a\cdot h_{a}}$ ${\displaystyle a}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle h_{a}}$

${\displaystyle a=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{51}}\right)}$

${\displaystyle h_{a}=r=R\cdot \cos \left({\frac {180^{\circ }}{51}}\right)\;}$ from this follows for the area of ​​a partial triangle

${\displaystyle {\begin{aligned}A_{\Delta }&={\frac {1}{2}}\cdot R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{51}}\right)\cdot R\cdot \cos \left({\frac {180^{\circ }}{51}}\right)\end{aligned}}\;}$ summarized it results

${\displaystyle A_{\Delta }=R^{2}\cdot \sin \left({\frac {180^{\circ }}{51}}\right)\cdot \cos \left({\frac {180^{\circ }}{51}}\right)}$

${\displaystyle A_{\Delta }\approx 0{,}0614441\cdot R^{2}}$

and for the area of ​​the entire 51 gon

${\displaystyle A=51\cdot A_{\Delta }=51\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{51}}\right)\cdot \cos \left({\frac {180^{\circ }}{51}}\right)}$

${\displaystyle A\approx 3{,}133651\cdot R^{2}}$

construction

As described above in the regular 51-square , the 51-square can be displayed as a construction with compass and ruler . Since the number of its vertices results from the multiplication of the two Fermat prime numbers and , the regular 51-vertex can be found by expanding an already known construction of the seventeen- sided. The two polygons triangle and seventeenth-corner (the number of sides corresponds to the Fermat prime numbers or ) are placed on top of each other symmetrically with regard to their central angles in the common circumference, as is shown e.g. B. Johannes Kepler shows in his work WELT-HARMONIK in the construction of the fifteen -sided . ${\displaystyle 3}$ ${\displaystyle 17}$ ${\displaystyle 3}$ ${\displaystyle 17}$

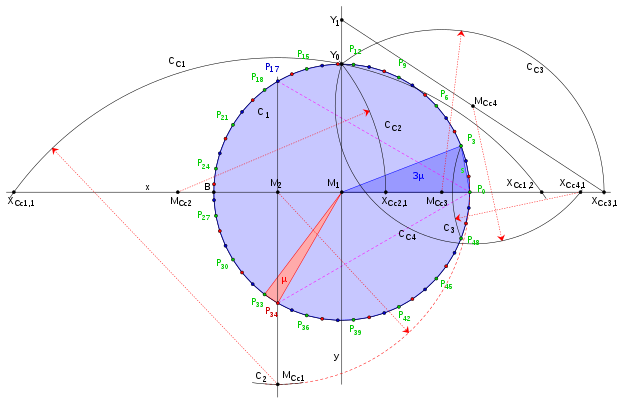
In principle, one of the three methods described in Siebzehneck can be selected as the basis for the construction . For reasons of the very little effort required, the method of Duane W. DeTemple , from 1991, is used.

Preliminary considerations

Fig. 1: Seventeen-corner after Duane W. DeTemple

In the drawing, the Siebzehnecks by Duane W. Detemple (Figure 1) which is well recognizable, Mittelsenkrechte from cuts not only the arc but also the perimeter. If this intersection point is marked as, it lies directly next to the corner point. This results in the central angle with the angular width of an equilateral triangle , which is added geometrically clockwise to the central angle of the seventeenth- corner . ${\displaystyle Q'}$ ${\displaystyle c_{2},}$ ${\displaystyle P_{34}}$ ${\displaystyle P_{11}.}$ ${\displaystyle P_{34}OP_{0}}$ ${\displaystyle 120^{\circ }}$

Hence for

Central angle of the circular sector ${\displaystyle \theta _{1}}$ ${\displaystyle OP_{11}P_{0}}$

${\displaystyle \theta _{1}={\frac {6}{17}}\cdot 360^{\circ }=127{,}0588235294117647\ldots ^{\circ },}$

Central angle of the circular sector ${\displaystyle \theta _{2}}$ ${\displaystyle OP_{11}P_{34}}$

${\displaystyle \theta _{2}={\frac {6}{17}}\cdot 360^{\circ }-120^{\circ }=7{,}0588235294117647\ldots ^{\circ },}$ because of

Central angle of the 51 gon ${\displaystyle \mu }$

${\displaystyle \mu ={\frac {360^{\circ }}{51}}=7{,}0588235294117647\ldots ^{\circ }}$ also applies

${\displaystyle \theta _{2}=\mu .}$

Thus, the line is a side length and a corner point of the 51-gon sought. ${\displaystyle {\overline {P_{11}P_{34}}}}$ ${\displaystyle a}$ ${\displaystyle P_{34}}$

The position of the corner point of the 51-gon also results from the number of side lengths contained in the central angle ${\displaystyle P_{34}}$ ${\displaystyle a_{A}}$ ${\displaystyle 120^{\circ }}$

${\displaystyle a_{A}={\frac {120^{\circ }}{7{,}0588235294117647}}=17,}$ it follows

starting from the corner point not counted , the clockwise 17th corner point corresponds to the corner point that is counted counterclockwise. ${\displaystyle P_{0},}$ ${\displaystyle P_{34}}$

The 17th corner point of the 51 corner is therefore exactly opposite the 34th corner point in relation to the central axis . ${\displaystyle {\overline {QP_{0}}}}$

Construction description

The identifiers in Figure 2 that have been changed compared to the original correspond to those used today.

Image 2: Extension of the construction of the 17-sided according to Duane W. DeTemple to the construction of the 51-sided by adding the corners of the equilateral triangle ( - - ) and removing the missing points ${\displaystyle P_{0}}$ ${\displaystyle P_{17}}$ ${\displaystyle P_{34}}$

• Draw a straight line (analytically an X-axis) and determine a point on it, the later center point of the polygon (analytically a coordinate origin). ${\displaystyle x}$ ${\displaystyle M_{1}}$
• Drawing a circle as a radius (analytically a unit circle) around . There are two intersection points , the corner point of the polygon and the counterpoint . ${\displaystyle C_{1}}$ ${\displaystyle M_{1}}$ ${\displaystyle P_{0}}$ ${\displaystyle B}$
• Establishing the vertical (analytically a Y-axis) on the straight line in . The point of intersection results . ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle M_{1}}$ ${\displaystyle Y_{0}}$
• Halving the distance in . ${\displaystyle {\overline {BM_{1}}}}$ ${\displaystyle M_{2}}$
• Establishing the perpendicular on the straight line in . The two intersections with are the corner points and of the 51 corner. ${\displaystyle M_{2}}$ ${\displaystyle C_{1}}$ ${\displaystyle P_{17}}$ ${\displaystyle P_{34}}$
• Draw the arc around with the radius . The intersection with the vertical is . ${\displaystyle C_{2}}$ ${\displaystyle M_{2}}$ ${\displaystyle {\overline {M_{2}P_{0}}}}$ ${\displaystyle M_{Cc1}}$
• Now the first Carlyle circle is drawn through the point ; the intersections are and . ${\displaystyle M_{Cc1}}$ ${\displaystyle C_{C1}}$ ${\displaystyle Y_{0}}$ ${\displaystyle X_{Cc1,1}}$ ${\displaystyle X_{Cc1,2}}$
• The route is halved. One receives . ${\displaystyle {\overline {M_{1}X_{Cc1,1}}}}$ ${\displaystyle M_{Cc2}}$
• Draw a second Carlyle-circle around through . The points of intersection with x are the points and (the latter is not shown as it is no longer required). ${\displaystyle C_{C2}}$ ${\displaystyle M_{Cc2}}$ ${\displaystyle Y_{0}}$ ${\displaystyle X_{Cc2,1}}$ ${\displaystyle X_{Cc2,2}}$
• The route is halved. One receives . ${\displaystyle {\overline {M_{1}X_{Cc1,2}}}}$ ${\displaystyle M_{Cc3}}$
• Drawing a third Carlyle circle around through . The points of intersection with x are the points and (the latter is also not shown as it is no longer required). ${\displaystyle C_{C3}}$ ${\displaystyle M_{Cc3}}$ ${\displaystyle Y_{0}}$ ${\displaystyle X_{Cc3,1}}$ ${\displaystyle X_{Cc3,2}}$
• Removal of the route on from from from. You get point ${\displaystyle {\overline {M_{1}X_{Cc2,1}}}}$ ${\displaystyle y}$ ${\displaystyle Y_{0}}$ ${\displaystyle Y_{1}}$
• Connect the points and with a segment. ${\displaystyle Y_{1}}$ ${\displaystyle X_{Cc3,1}}$
• Halve the route . You get point . ${\displaystyle {\overline {Y_{1}X_{Cc3,1}}}}$ ${\displaystyle M_{Cc4}}$
• Drawing a fourth Carlyle circle around through . The points of intersection with x are the points and (the latter is not labeled as it is no longer needed). ${\displaystyle C_{C4}}$ ${\displaystyle M_{Cc4}}$ ${\displaystyle Y_{0}}$ ${\displaystyle X_{Cc4,1}}$ ${\displaystyle X_{Cc4,2}}$
• Draw an arc around with the perimeter radius . The intersection points with the circumference are the two adjacent points of the 17-sided and thus the points and the 51-sided. ${\displaystyle X_{Cc4,1}}$ ${\displaystyle {\overline {M_{1}B}}}$ ${\displaystyle C_{1}}$ ${\displaystyle P_{0}}$ ${\displaystyle P_{3}}$ ${\displaystyle P_{48}}$
• By repeating the distance on the perimeter , starting with , you get the missing points of a regular 17-gon. Up to this point the construction corresponds to that of the 17-sided. ${\displaystyle {\overline {P_{0}P_{3}}}}$ ${\displaystyle C_{1}}$ ${\displaystyle P_{0}}$
• By repeatedly subtracting the distance from the perimeter , starting from the points (blue) and (red), you get all the missing corner points of the 51 corner, which can be connected to each other to form the 51 corner. ${\displaystyle {\overline {P_{0}P_{3}}}}$ ${\displaystyle C_{1}}$ ${\displaystyle P_{17}}$ ${\displaystyle P_{34}}$

Occurrence

architecture

RWE tower in Essen

The cross-section of the RWE tower in Essen is a regular 51-corner.

literature

• H. Maser: Die Teilung des Kreises ..., Article 365. , in Carl Friedrich Gauss' studies on higher arithmetic , published by Julius Springer, Berlin 1889; Göttingen Digitization Center, University of Göttingen; accessed on March 15, 2018.

Individual evidence

1. ↑ Johannes Kepler: WORLD HARMONICS. XLIV. Sentence., Page of the Fifteenth, Page 44. In: Google Books. R. OLDENBURG VERLAG 2006, translated and introduced by MAX CASPAR 1939, p. 401 , accessed on February 21, 2018 . 
2. ↑ Duane W. Detemple: Carlyle Circles and the Lemoine Simplicity of Polygon Constructions. ( Memento of August 11, 2011 in the Internet Archive ). The American Mathematical Monthly, Vol. 98, No. 2 (Feb., 1991), pp. 101-104 ( JSTOR 2323939 ) accessed on February 16, 2018.