Nineteenth

Regular nineteenth corner

A nineteenth corner , also known as a Nonadekagon ( English also enneadecagon, enneakaidecagon ), is a polygon with 19 sides and 19 corners. Often a flat, regular nineteenth corner is meant with all sides of the same length and all corner points on a common perimeter .

Regular nineteenth corner

According to Carl Friedrich Gauß and Pierre-Laurent Wantzel, the regular nineteenth corner is not a constructible polygon , because its number of sides is not a product of a power of two with pairwise different Fermat prime numbers . ${\displaystyle n=19}$

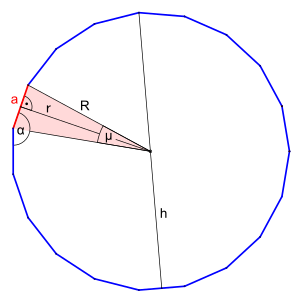
Sizes

Sizes of a regular nineteenth
Interior angle	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {17}{19}}\cdot 180^{\circ }\\\alpha &=161{,}{\overline {052631578947368421}}^{\circ }\end{aligned}}}$
Central angle (Center angle)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{19}}\\\mu &=18{,}{\overline {947368421052631578}}^{\circ }\end{aligned}}}$
Side length	${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{19}}\right)\\a&\approx 0{,}329189\cdot R\end{aligned}}}$
Perimeter radius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{19}}\right)}}\\R&\approx {\frac {a}{0{,}329189}}\end{aligned}}}$
Inscribed radius	${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {180^{\circ }}{19}}\right)\\r&\approx 0{,}986361\cdot R\end{aligned}}}$
height	${\displaystyle {\begin{aligned}h&=R+r=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{19}}\right)\right)\\h&\approx 1{,}986361\cdot R\end{aligned}}}$
Area	${\displaystyle {\begin{aligned}A&=19\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{19}}\right)\cdot \cos \left({\frac {180^{\circ }}{19}}\right)\\A&\approx 3{,}084645\cdot R^{2}\end{aligned}}}$

Mathematical relationships

Interior angle

The interior angle is enclosed by two adjacent sides of the length . ${\displaystyle \alpha }$ ${\displaystyle a}$

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {19-2}{19}}\cdot 180^{\circ }={\frac {17}{19}}\cdot 180^{\circ }=\left(161{\frac {1}{19}}\right)^{\circ }}$

Central angle

The central angle or center angle is enclosed by two adjacent circumferential radii of the length . ${\displaystyle \mu }$ ${\displaystyle R}$

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{19}}=\left(18{\frac {18}{19}}\right)^{\circ }}$

Side length

The side length is calculated as follows ${\displaystyle a}$

${\displaystyle a=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{19}}\right)}$.

Perimeter radius

The radius of the perimeter results from transforming the formula for the side length to ${\displaystyle R}$ ${\displaystyle a}$

${\displaystyle R={\frac {a}{2}}\cdot \csc \left({\frac {180^{\circ }}{19}}\right)}$.

Inscribed radius

The incircle radius is the height of an isosceles partial triangle with the two legs equal to the circumferential radius and the base line equal to the side length : ${\displaystyle r}$ ${\displaystyle R}$ ${\displaystyle a}$

${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {\mu }{2}}\right)=R\cdot \cos \left({\frac {180^{\circ }}{19}}\right)\end{aligned}}}$

height

The height of a regular nineteenth corner results from the sum of the incircle radius and the circumferential radius : ${\displaystyle h}$ ${\displaystyle r}$ ${\displaystyle R}$

${\displaystyle h=R+r=R+R\cdot \cos \left({\frac {180^{\circ }}{19}}\right)=R\cdot \left(1+\cos \left({\frac {180^{\circ }}{19}}\right)\right)}$

Area

The area of ​​a triangle is generally calculated as . The results of the side length and the incircle radius are used to calculate the nineteenth triangle , where the following is used for the height : ${\displaystyle A_{\Delta }={\tfrac {1}{2}}a\cdot h_{a}}$ ${\displaystyle a}$ ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle h_{a}}$

${\displaystyle a=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{19}}\right),}$

${\displaystyle h_{a}=r=R\cdot \cos \left({\frac {180^{\circ }}{19}}\right),}$ from this follows for the area of ​​a partial triangle

${\displaystyle A_{\Delta }={\frac {1}{2}}\cdot R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{19}}\right)\cdot R\cdot \cos \left({\frac {180^{\circ }}{19}}\right),}$ summarized it results

${\displaystyle A_{\Delta }=R^{2}\cdot \sin \left({\frac {180^{\circ }}{19}}\right)\cdot \cos \left({\frac {180^{\circ }}{19}}\right)}$ and for the area of ​​the whole nineteenth

${\displaystyle A=19\cdot A_{\Delta }=19\cdot R^{2}\cdot \sin \left({\frac {180^{\circ }}{19}}\right)\cdot \cos \left({\frac {180^{\circ }}{19}}\right).}$

Geometric constructions

A regular nineteenth corner cannot be constructed with a compass and ruler . However, if you use an additional tool such as B. the tomahawk for the exact trisection of an angle or a special curve ruler with the curve shape of the Archimedean spiral or the quadratrix of Hippias for the division of the 90-degree angle into equal angles , an exact solution is feasible . ${\displaystyle n}$

In order to be able to use the tomahawk to determine the central angle , a possibly complicated construction of at least a suitable angle width is required, as can be seen in the example of the triangle by Andrew M. Gleason .

In contrast, both the Archimedean spiral and the quadratrix of Hippias offer a simple and short path - it leads by dividing a line into parts of equal length and then projecting four of these parts into the selected curve - to find the central angle sought. ${\displaystyle n}$

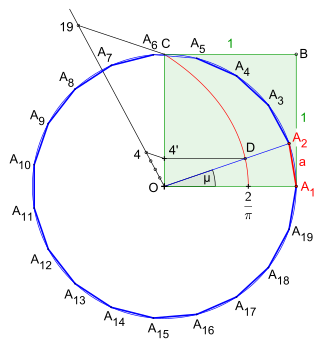
Quadratrix des Hippias as an additional aid

Image 1: Regular nineteenth-corner with a given circumference as an exact construction with the quadratic rix of Hippias as an additional aid

The construction (picture 1) is almost identical to that of the elf .

After drawing the square z. B. with the side length and the construction of the special curve, the so-called quadratic rix of Hippias , with the parametric representation : ${\displaystyle 1}$ ${\displaystyle \gamma \colon (-\pi ,\pi )\to \mathbb {R} ^{2}}$

${\displaystyle \gamma (t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}t\cot \left({\frac {\pi }{2}}t\right)\\t\end{pmatrix}},\quad 0\leq t\leq 1}$

the route is divided into nineteen equally long sections using the route division. For the sake of clarity, only the relevant points are shown in the drawing. ${\displaystyle {\overline {CO}}}$

The central angle of the nineteenth corner results from, however, the quadratrix of Hippias only subdivides the angles down to equal angles. It follows that a nineteenth of the distance can only achieve a nineteenth of the angle . Therefore, because of the calculation of the central angle from the circumference with its four times a nineteenth, i.e. H. the dividing point of the line used to construct the central angle . This arises after the construction of a parallel to from to the curve of the quadratrix, which results in the point . Now you draw a half line from the angle point through to the perimeter. ${\displaystyle \mu ={\tfrac {360^{\circ }}{19}},}$ ${\displaystyle >0^{\circ }}$ ${\displaystyle \leq 90^{\circ }}$ ${\displaystyle {\overline {CO}}}$ ${\displaystyle 90^{\circ }}$ ${\displaystyle \mu }$ ${\displaystyle 360^{\circ }}$ ${\displaystyle 4'}$ ${\displaystyle {\overline {CO}},}$ ${\displaystyle \mu }$ ${\displaystyle {\overline {A_{1}O}}}$ ${\displaystyle 4'}$ ${\displaystyle D}$ ${\displaystyle O}$ ${\displaystyle D}$

This results in the central angle and the second corner point on the circumference . The length of the line is the exact length of the side of the regular nineteenth corner. ${\displaystyle \mu }$ ${\displaystyle A_{2}}$ ${\displaystyle {\overline {A_{1}A_{2}}}}$ ${\displaystyle a}$

Approximation construction

Figure 2: Nineteenth-corner, approximation construction with a universal method

Fig. 2 shows a nineteenth-octagon around it, created with a universal method.

First, the diameter is divided into parts of equal length with the aid of the theorem of rays (not shown in the drawing) or determined by stringing together equally long distances. Now either the even or the odd numbers (division points) are marked on the diameter . In this example the even numbers and are entered. The subsequent halving of is done with the help of the two arcs around or with the radius . The arcs intersect at the points and by connecting them you get the center point and the central axis . ${\displaystyle {\overline {AB}}}$ ${\displaystyle 19}$ ${\displaystyle 19}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle 2,4,6,8,10,12,14,16}$ ${\displaystyle 18}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle C}$ ${\displaystyle D.}$ ${\displaystyle O}$ ${\displaystyle CD}$

After drawing in the radius around by it continues with setting the key points on the perimeter. The ruler is placed on the point and on the even number . Then draw a short line along the ruler through the opposite half of the circumferential line, results in the corner point of the nineteenth- corner . This procedure is repeated when determining the corner points. It is continued, starting from the point until the remaining corner points are found. Finally, the neighboring corner points are connected to one another. ${\displaystyle O}$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle 2}$ ${\displaystyle E_{1}}$ ${\displaystyle E_{2},\dotsc ,E_{9}.}$ ${\displaystyle D,}$ ${\displaystyle E_{10},\dotsc ,E_{18}}$

The special feature of this method is that nine sides of the nineteenth have the same length in pairs, e.g. B. the pages and . The length of the side is different from the others. ${\displaystyle {\overline {E_{1}E_{2}}}}$ ${\displaystyle {\overline {E_{17}E_{18}}}}$ ${\displaystyle {\overline {E_{9}E_{10}}}}$

The amount according to the largest, second smallest and smallest absolute error of the side lengths of the nineteenth corner for a circumferential radius with : ${\displaystyle R=1\;\mathrm {m} }$

${\displaystyle \approx 19{,}2\;\mathrm {mm} }$ at ${\displaystyle {\overline {E_{9}E_{10}}}}$

${\displaystyle \approx -1{,}25\;\mathrm {mm} }$at and ${\displaystyle {\overline {E_{3}E_{4}}}}$ ${\displaystyle {\overline {E_{15}E_{16}}}}$

${\displaystyle \approx 1{,}11\;\mathrm {mm} }$at and ${\displaystyle {\overline {E_{4}E_{5}}}}$ ${\displaystyle {\overline {E_{14}E_{15}}}}$

If you look at the two smallest absolute errors in terms of amount on the neighboring sides, it follows that both are almost equally distant from an ideal center . That means, if one would use this approximation construction z. B. only construct the lines (light brown) and (light blue), then constructively determine the arithmetic mean of these lines, this would result in a side length of the nineteenth triangle with a deviation of around ${\displaystyle 0\;\mathrm {mm} }$ ${\displaystyle {\overline {E_{3}E_{4}}}}$ ${\displaystyle {\overline {E_{4}E_{5}}}}$ ${\displaystyle a}$

${\displaystyle {\frac {1}{2}}\cdot \left(-1{,}25\;\mathrm {mm} +1{,}11\;\mathrm {mm} \right)=-0{,}07\;\mathrm {mm} }$.

Or to put it another way, with a circumcircle radius the deviation would be the constructed first side . ${\displaystyle R=100\;\mathrm {m} }$ ${\displaystyle \approx 7\;\mathrm {mm} }$

Occurrence

Church of the Redeemer in Ani

Church of the Redeemer in Ani,		another look at the church

The church is located in the east of the place Ani , the capital of the former Kingdom of Armenia , in the far east of today's Turkey in the province of Kars on the border with Armenia.

On the website VirtualANI.org the architecture of the church is described as follows (free translation):

"Architecture

The church is roughly circular with the lower half of the exterior divided into a 19-sided polygon . The very large (and very wide) drum [upper half] is unusually not divided into a polygon, but is a perfect circle. It is broken up by 12 narrow windows and has a semicircular dome on the inside. The church has only one entrance, in the south facade, through a monumental rectangular door topped with an architrave of pseudo-antique carvings. The interior had eight apses , with the altar apse much larger than the others. On both sides of the altar apse there were tiny chapels that were worked into the wall thickness. These chapels and the enlarged apse probably weakened the structure in such a way that damage was caused here, which ultimately led to the collapse of the church. "

Regular overturned nineteenth corners

A regular, overturned nineteenth corner results when at least one is skipped over each time when connecting the nineteen corner points and the chords thus created are of the same length. Such regular stars are noted with Schläfli symbols , indicating the number of corner points and connecting every -th point. ${\displaystyle \left\{n/k\right\}}$ ${\displaystyle n}$ ${\displaystyle k}$

In the following gallery the eight possible regular nineteen-ray stars, also called Enneadekagrams, are shown.

• Regular nineteen-ray stars
• 

  ${\displaystyle \left\{19/2\right\}{,}\ \left\{19/17\right\}}$

• 

  ${\displaystyle \left\{19/3\right\}{,}\ \left\{19/16\right\}}$

• 

  ${\displaystyle \left\{19/4\right\}{,}\ \left\{19/15\right\}}$

• 

  ${\displaystyle \left\{19/5\right\}{,}\ \left\{19/14\right\}}$

• 

  ${\displaystyle \left\{19/6\right\}{,}\ \left\{19/13\right\}}$

• 

  ${\displaystyle \left\{19/7\right\}{,}\ \left\{19/12\right\}}$

• 

  ${\displaystyle \left\{19/8\right\}{,}\ \left\{19/11\right\}}$

• 

  ${\displaystyle \left\{19/9\right\}{,}\ \left\{19/10\right\}}$

literature

• H. Maser: The division of the circle ..., Article 365. In: Carl Friedrich Gauss' investigations on higher arithmetic. Published by Julius Springer, Berlin 1889; Göttingen Digitization Center, University of Göttingen; accessed on March 15, 2018.

Web links

Commons : Regular nineteenth-corner  collection of images, videos, and audio files

• Partial plan of the nineteenth fortress
• Nineteenth corner, variant of the approximate construction with a universal method

Individual evidence

1. ^ Eric W. Weisstein: CRC Concise Encyclopedia of Mathematics. P. 914 Enneadecagon. 2003, accessed January 28, 2018.
2. ↑ William Templeton: The millwright & engineer's pocket companion. P. 48 Nonadecagon. 1852, Retrieved January 28, 2018.
3. ^ Rieke Deimer: The Quadratrix. In: Mathematics / Algebraic Geometry, Selected Higher Curves WS2016-17. University of Mainz, January 6, 2017, accessed on January 28, 2018 . 
4. ↑ Hans-Wolfgang Henn: Elementary Geometry and Algebra. Vieweg + Teubner Verlag, 2003, pp. 45-48. Page 46 ff. Quadratrix ( excerpt (Google) ), accessed on January 29, 2018.
5. ↑ Horst Hischer: Mathematik in der Schule 32 (1994) 5. History of mathematics as a didactic aspect (2). Solution of classic problems. P. 279 ff. , Accessed on January 29, 2018 . 
6. ^ H. August: Drawing construction of an elf. In: Drawing constructions: polygons. Retrieved February 5, 2018 . 
7. ^ Peter Eckardt: Siebeneck. In: Stars and Polygons. Retrieved February 5, 2018 . 
8. ↑ Steven Sim: THE CHURCH OF THE REDEEMER (SURP AMENAP'RKITCH). VirtualANI, accessed July 13, 2018 .  From the Internet Archive