Squaring the square

from Wikipedia, the free encyclopedia
21 squares, all of different sizes, seamlessly join together to form a large square.
[1] Simple , perfect squaring of the lowest possible order (21)

The squaring of the square is understood to mean the gapless and overlap-free coverage (" tiling ") of a given square with smaller squares whose side lengths have integral values. The term " squaring the square" was chosen as a joking reference to the squaring of the circle , although the two problems have nothing to do with each other.

properties

13 squares, mostly of different sizes (some appear twice), seamlessly join together to form a large square.
[2] Simple , imperfect quadrature of the lowest possible order (13)
24 squares, all of different sizes, fit together seamlessly to form a large square; some squares form a smaller square inside the large one.
[3] Perfect , composite quadrature of the order 24

Side lengths

In 1903, the German geometer Max Dehn proved that the sides of a rectangle tiled with squares (including those of a square) must be commensurate with the sides of the partial squares . This means that the side lengths of the squared rectangle and those of all partial squares are integer multiples of a single number ; With a suitable choice of the unit of length, all side lengths are then whole numbers.

order

As order (Engl. Order ) a tiling is defined as the number of sub-squares.

Additional conditions

Trivial examples of parquet flooring by and with squares can be found in many everyday things - such as the chessboard or on every kitchen wall tiled with square tiles . The following additional conditions make the task interesting and demanding:

  • No two sub-squares should be the same size. A square tiling that meets this requirement is called perfect .
  • As long as a subset of the sub-squares forms a rectangle, called the quadrature composed (Engl. Compound , otherwise) - this is the more difficult case - just (. Engl simple ).

For imperfect tiling, i.e. those that contain several congruent partial squares, further additional conditions are considered:

  • Nowhere-neat tiling - no two sub- squares of the same size have an entire side in common.
  • No touch tiling - no two partial squares of the same size have even part of one side in common.

It is evident that the no-touch variants are a subset of the Nowhere neat tiling.

Examples

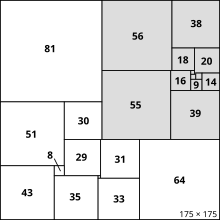
Figure 1 shows the perfect and at the same time simple tiling of the lowest order (21), Figure 2 the simple , imperfect squaring of the lowest possible order 13 (it is also of the no touch tiling type , since the sub-squares of the same size do not touch each other), Figure 3 a perfect but composite quadrature of order 24 (the gray-shaded tiles in the top right combine to form a rectangle).

Mrs. Perkins's quilt

The simple, illustrative drawing shows the quilt, composed of differently patterned squares of fabric, which hangs on a wall on 2 nails. The solution to the problem is indicated by different coloring of partial squares.
Mrs. Perkins's Quilt (solution)

As "Mrs. Perkins's Quilt ”is the name given to the division of a given square into the smallest possible number of sub-squares, without this quadrature having to be perfect or simple . The name goes back to a puzzle that the American puzzle author Samuel Loyd and the British entertainment mathematician Ernest Dudeney published in 1917. In this exercise, a square quilt made of 169 (13 × 13) squares of the same size is to be cut along the seams into the smallest possible number of square pieces. The solution (see picture) has order 11; Since two congruent parts (the two yellow ones at the top) border each other with a whole square side, it is neither simple (the two squares form a rectangle) nor perfect , nor does it have the properties nowhere-neat or even no touch .

history

The square, light gray stamp shows an approximately square area composed of 11 colored squares
Special stamp from 1998 for the International Congress of Mathematicians in Berlin. The tiled area is only apparently a square (the side lengths are actually 177 and 176).

It may come as a surprise that research into the rather elementary and seemingly simple problem of squaring the square dates back to the last century. Since then, several million squares of different types and orders have been discovered and documented, with the starting point of this development initially being the search for the tiling of rectangles (not to be confused with the squaring of the rectangle ).

Some milestones in this history of discovery are just a few examples.

  • 1903 - Max Dehn proves that a rectangle can be squared if and only if its sides are commensurable.
  • 1936 - The four British mathematicians William Thomas Tutte , R. Leonard Brooks , Arthur Harold Stone and Cedric Smith , who publish under the common pseudonym " Blanche Descartes ", fail to prove their conjecture that squares cannot be broken down into a finite number of different sub-squares. They connected the problem of squaring rectangles and squares to electrical flows in graphs. In 1940 they gave an example of squaring a square with 69 squares.
  • 1939 - The German mathematician Roland Sprague succeeds in the first squaring of a square, it is perfect and composed , has order 55 and side length 4205.
  • 1939 - R. Leonard Brooks publishes the first perfect and at the same time simple quadrature (order 38, side length 4920).
  • 1948 - Theophilus Willcocks finds a quadrature with 24 squares.
  • 1978 - AJW Duijvestijn finds the perfect and simple quadrature of order 21 with the help of a computer (Figure 1 above) and proves that this is the solution of the lowest possible order and at the same time the only one of this order. (He showed that you need at least 21 as early as 1962.)

A rectangle was squared as early as 1925 by the Polish mathematician Zbigniew Morón . In 2008, Frederick and James Henle succeeded in completely breaking down the plane with squares with sides 1,2,3, 4 and so on. In 1993 SJ Chapman found a decomposition of a Möbius strip with five squares of different sizes. You need at least nine squares to make a cylinder.

See also

Individual evidence

(For sources see literature and web links.)

  1. ↑ a b Darling 2004, p. 302
  2. ↑ Stewart 1998, p. 10
  3. ↑ a b c d Anderson 2014, Honsberger 2002
  4. ↑ Scherer , Devincentis
  5. ↑ a b Anderson 2014
  6. ↑ Sprague 1939
  7. ^ Ian Stewart , Professor Stewart's mathematical hodgepodge, Rowohlt 2011
  8. ↑ Duijvestijn 1978
  9. ↑ Henle, Henle, Squaring the plane, American Math. Monthly, Volume 115, 2008, pp 3-12
  10. ^ Clifford Pickover, Math Book, Sterling Publ., P. 352

literature

Web links

Commons : Squaring the Square  - Collection of Images