Magic square

16 5 9 4th 2 11 7th 14th 3 10 6th 15th 13 8th 12 1

Yang Hui Square

A magic square is a square arrangement of numbers or letters that meet certain requirements.

definition

The definition of a normal magic square is:

“A magic square of the edge length is a square arrangement of the natural numbers so that the sum of the numbers in all rows, columns and the two diagonals is the same. This sum is called the magic number of the magic square. " ${\displaystyle n}$ ${\displaystyle 1,2,\dotsc ,n^{2}}$

The edge length is used as the order of the magic squares. ${\displaystyle n}$

It can also be seen that any arithmetic sequence is suitable for a magic square. There are still numerous variants of magic squares for which not all of these conditions are met or additional restrictions are required (see below ).

Semimagic square

Number squares where the two diagonals do not also result in the magic number or the target sum are considered unsuccessful and dissonant . They strive to resolve the contradiction. These failed number squares are called semi magic squares.

3rd order semimagic square with the 7 in the middle field and the numbers 1 to 9.

9	2	4th
5	7th	3
1	6th	8th

There are two ways of resolving the contradiction with squares of the third order. The first way is to adjust the middle element while maintaining the target amount. The second way changes the target total with the middle element unchanged. One can always find real solutions with agreement of three elements. Solutions with more than three matching elements are therefore of interest.

Calculating the magic number

The total of the series is called the magic number . It's easy to see that the magic number has to be times the sum of the numbers from 1 to : ${\displaystyle 1/n}$ ${\displaystyle n^{2}}$

${\displaystyle S_{n}={\frac {1}{n}}\cdot \sum _{x=1}^{n^{2}}x={\frac {1}{n}}\cdot {\frac {n^{2}(n^{2}+1)}{2}}={\frac {n(n^{2}+1)}{2}}={\frac {n^{3}+n}{2}}}$

Because: be the sum of the numbers in a line. We have lines that should all have the same line total; and the sum over all lines, i.e. , is equal to the sum of all entries in the square, i.e. identical to ( Gaussian sum formula ). ${\displaystyle ZS}$ ${\displaystyle n}$ ${\displaystyle n\cdot ZS}$ ${\displaystyle \textstyle \sum _{k=1}^{n^{2}}k={\frac {n^{2}\cdot (n^{2}+1)}{2}}}$

The first magic numbers starting with are ${\displaystyle n=0}$

0, 1, 5, 15, 34, 65, 111, 175, 260, 369, 505, ... (sequence A006003 in OEIS ).

The first three terms in this are hypothetical. A magic square with edge length 1 is trivial. For edge length 2 there is no solution with four different numbers.

Equivalence and standard form

It is obvious that rotation by 90 °, 180 ° and 270 ° as well as reflection on the main axes and diagonals turns a magic square into a magic square. These eight magic squares are equivalent; it is enough to examine one of them. It has become common practice to use the standard Frénicle form here :

• The element in the upper left corner [1,1] is the smallest of the four elements in the corners.
• The element to the right of it [1,2] is smaller than the element below [2,1].

Complement of the normal magic square

Any normal magic square can be complemented. To form the complementary square, all entries must be multiplied by −1 and then the constant added to each entry . The elements in the starting square and in the complement complement each other . The complementary square has the same structure as the starting square. The complement formation is not an exchange operation, as it is not independent of the structure of the starting square. Magic squares with certain structures can be self-complementary, i. That is, the complement is then equivalent to the starting square. Of the 12 structures of order 4, the magic squares of the 3rd and 6th structure are self-complementary. ${\displaystyle n^{2}+1}$ ${\displaystyle n^{2}+1}$

Comparison of magic squares

The exact comparison is made by classifying the magic squares in the solution set of the homogeneous linear system of equations. This corresponds to the classification in the non-geometric vector space. Every magic square has its precisely definable place in the solution set. The solution set is an excellent example of a non-geometric vector space. In the case of magic squares of a higher order, the method of classification reaches the limits of the imagination. However, it is didactically very interesting for 3rd and 4th order magic squares. In the case of a higher order, one has to resort to structural analysis and the method of correlation .

Magic square structure

All magic squares have an internal structure. These structures are different depending on the order of the square and become more and more complex with increasing order. For normal 4th order magic squares there are exactly 12 structure groups with identical pair sums. These are also called Dudeney patterns after their discoverer Henry Dudeney . The images of the structures can be used to analyze the symmetry properties of the magic squares.

Special magic squares

General real squares

General real squares consist of real numbers . Your only requirement is that rows, columns, and diagonals make the same sum . The amount is freely selectable. General real squares are the solution sets of a homogeneous system of linear equations . The system of equations has linear equations. ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle 2n+2}$

Example of a result of the third order solution set and : ${\displaystyle s=1,5}$

−0.5	2	0
1	0.5	0
1	−1	1.5

An outstanding property of general third-order real number squares is that the middle number element always contains the arithmetic mean of all numbers in the square. The middle number element is therefore not only the mean value from the spatial concept , but also from the numerical concept at the same time.

If you specify as a further condition that the number square only consists of natural numbers , you get a finite solution set for each target sum . For 3rd order squares and there are 25 solutions (15 with and 10 without repetition of numbers). ${\displaystyle s}$ ${\displaystyle s=27}$

14th	7th	6th
1	9	17th
12	11	4th

The target sum is a free variable of the solution set of the homogeneous linear equation system. You can therefore use the calculated magic number for the target total. With the magic number 15 you get 9 solutions (8 with and 1 without repetition of numbers). This is the Lo-Shu and his court. ${\displaystyle s}$ ${\displaystyle s}$

Symmetrical magic squares

If a magic square also fulfills the condition that the sums of two elements that are point-symmetrical to the center point (for even) or to the central element (for odd magic squares) are equal, it is called a symmetric magic square . It is more accurate to use the term centrally symmetric magic square or associative magic square . As can easily be shown, the sum of two such elements must be; for odd symmetrical magic squares, the middle field has the value . Symmetric magic squares have the simplest internal structure of the magic squares. The 3 by 3 magic square is a symmetrical magic square. In the case of the 4 by 4 magic squares, only one of the 12 structural groups (group 3) is the group of symmetrical magic squares. It is the star-shaped representation in the structural diagrams. ${\displaystyle n^{2}+1}$ ${\displaystyle (n^{2}+1)/2}$

In the case of symmetrical magic squares, the complement of the starting square can always be mapped onto the starting square by rotating it by 180 °. that is, all symmetric magic squares are self-complementary (self-similar).

Pandiagonal magic squares

Example of a pandiagonal magic square

In the case of a pandiagonal magic square , not only the sum of the diagonals but also that of the broken diagonals must be the same. The broken diagonals run parallel to the main or opposite diagonal , with elements outside the square being shifted by one edge length. In contrast to symmetrical magic squares, squares with a pandiagonal property cannot always read this special property directly from the image of the internal structure. The smallest possible order for squares with a pandiagonal property is the 4th order. The structure group 1 of the 4th order squares consists of the 48 pandiagonal squares. In the case of higher-order magic squares, there are several structural groups that consist of or contain squares with pandiagonal properties. The magic squares of the symmetrical structural group of the 5th order only partially have the pandiagonal property. The symmetrical structural group is a main structural group. For main structure groups, the mean value is in the middle of the square. At 5 times 5 this is the value 13. This definition ensures the undistorted representation of the internal structure. Every odd pandiagonal square can be brought into a square of this structure by shifting in the shifting cluster. There are three other main structural groups in the 5th order, which consist of pandiagonal squares. These undistorted structures are aesthetically pleasing and show the mathematical connection between averaging and symmetry. By moving in the displacement cluster, the secondary structure groups are formed for each main structure group.

Magic squares that are both symmetrical and pandiagonal are called ultramagic.

Magic prime squares

There are numerous variants of magic squares in which the requirement is dropped that only the numbers from 1 to should appear, but that additional conditions must be met. The best known of these are magic prime squares, where all elements must be prime numbers (or 1). ${\displaystyle n^{2}}$

The 3rd order magic prime number square with the smallest possible magic sum of 111 was discovered in 1900 by Henry Ernest Dudeney , who considered 1 to be the prime number. At that time it was considered to be the first magic prime number square in the solution set of general 3rd order magic squares.

67	1	43
13	37	61
31	73	7th

The first true 3rd order magic prime square has the smallest possible magic sum of 177.

17th	89	71
113	59	5
47	29	101

For the first time there are two different magic prime squares for the mean value 127 in the solution set of general magic squares of the 3rd order.

The number of normal magic squares

There is a (trivial) magic square with edge length 1, but none with edge length 2. Apart from symmetry operations or specified in the Frénicle standard form, there is also only one normal magic square with edge length 3 (see under Lo-Shu ). All 880 magic squares with edge length 4 were found by Frénicle de Bessy as early as 1693. With edge length 5 there are 275,305,224 magic squares; furthermore, no exact figures are known, but there are relatively reliable estimates up to about . The most extensive calculations were carried out by Walter Trump. The number of symmetrical, pandiagonal and ultramagic squares for smaller ones is also known, for example there are 48 symmetrical magic squares with edge length 4 and 16 ultramagic squares with edge length 5. ${\displaystyle n=20}$ ${\displaystyle n}$

Famous examples

The Lo-Shu

An example is the oldest known magic square from China around 2800 BC. In Europe it was in the 16./17. Century Saturn seal ( Heinrich Cornelius Agrippa von Nettesheim , approx. 1510 and Athanasius Kircher , Arithmologia 1665) called.

4th	9	2
3	5	7th
8th	1	6th

The Lo-Shu is the only normal 3 by 3 magic square.

Albrecht Dürer's magic square

Detail from Melencolia I

One of the most famous magic squares in Albrecht Dürer's engraving Melancholia I find.

16	3	2	13
5	10	11	8th
9	6th	7th	12
4th	15th	14th	1

properties

The Dürer's square has the following properties:

• It's a symmetrical magic square.

Normal symmetry properties of magic squares 4 by 4:

• The sum of the numbers in vertical or horizontal rows is always 34.
• The sum of the two middle diagonals is 34 each.
• The sum of the four corner fields and the four center fields is 34 each.
• The sum of the four opposing central edge fields is 34 ( and ). ${\displaystyle 5+9+8+12}$ ${\displaystyle 3+2+15+14}$

Additional symmetry properties of the Dürer square:

• The sum of the two diagonals broken in the middle is 34 each ( and ). ${\displaystyle 3+5+12+14}$ ${\displaystyle 2+8+9+15}$
• The sum of the elements of the four quadrants is 34 each.
• The sum of the four fields, each of which is offset by 1 or 2 clockwise from the four corner fields, is 34 ( and ). ${\displaystyle 8+14+9+3}$ ${\displaystyle 12+15+5+2}$
• The sum of the first two numbers of a row (e.g. the first) and the last two of the mirrored (e.g. the last) row (e.g. ) results in 34. This also applies accordingly to columns ( e.g. ). ${\displaystyle 16+3+14+1}$ ${\displaystyle 3+10+7+14}$
• The numbers in the middle two rows or columns in zigzag order add up to 34 (e.g. or ). The same also applies to the two outer rows or columns (e.g. ). ${\displaystyle 3+11+6+14}$ ${\displaystyle 9+10+7+8}$ ${\displaystyle 16+8+9+1}$
• The sum of each pair of numbers symmetrical about the center point is 17.

Due to the additional symmetry properties of the Dürer square, twin squares can be generated by means of exchange operations. Swapping column 2 with column 3 creates the square:

16	2	3	13
5	11	10	8th
9	7th	6th	12
4th	14th	15th	1

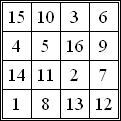
This twin square has identical symmetry properties. It is equivalent to the square of Yang Hui . Even Adam Ries used this square in his arithmetic book. It is shown mirrored on the main diagonal at the beginning of the article.

Another swap operation is the swap of columns 1 with 2 and at the same time columns 3 with 4. The third swap operation is the swap of two diagonal quadrants (blocks of four), e.g. B. from block 2 with block 3. The fourth swap operation is the swap of the four quadrants to four rows. The corner fields become the main diagonal and the fields of the core block become the opposite diagonal. The new magic square no longer has a match between the composition of the sums (rows, columns, diagonals) and the starting square. The swap operation quadrants to rows forms the basis for the proof that the sum of the elements in the respective quadrant in the centrally symmetric square 4 times 4 is also the magic number 34.

These swap operations are only possible with centrally symmetric magic squares 4 by 4. The new magic squares created with them can still be processed with the exchange operations. By chaining the mentioned exchange operations, all 48 centrally symmetric magic squares (4 × 4) can be generated.

Interpretations

• In the middle of the last line is the year 1514, the year in which Dürer made the engraving.
• At the beginning of the last line there is a 4, at the end a 1. If you equate these numbers with letters of the alphabet, you get D and A, the monogram of the artist (Dürer Albrecht)

The magic squares of the 16th and 17th centuries in Europe

In the 16./17. Century began an intensive occupation with magic squares. The polymaths Heinrich Cornelius Agrippa von Nettesheim and Athanasius Kircher developed several magic squares of a higher order (up to 9 by 9). Algorithms for creating even and odd magic squares have also been given in the works. The assignment of certain magic squares to stars goes back to Agrippa. The Jupiter square of Agrippa is identical to the 4 by 4 square of Yang Hui . The magic squares with the designation / assignment to stars were used on many amulets.

The magic square at the Sagrada Família

The magic square on the Passion facade of the Sagrada Família

The façade of the Sagrada Família in Barcelona , dedicated to the Passion , by the sculptor Josep Maria Subirachs , contains a magical square:

1	14th	14th	4th
11	7th	6th	9
8th	10	10	5
13	2	3	15th

It is not a magic square in the strict sense, because not all numbers from 1 to 16 appear (12 and 16 are missing), while 10 and 14 appear twice. The magic number is 33, an allusion to the age of Christ. The number square on the Sagrada Família can be generated by subtracting 1 for 4 elements from the Dürer's square. The values ​​of 12 elements therefore agree with the Dürer's square. The 4 changed elements were chosen so that all rows, columns, diagonals and blocks / quadrants can be reached once.

Elements in Dürer's square from whose value 1 is subtracted:

• e [1, 1] = 16
• e [2, 3] = 11
• e [3, 4] = 12
• e [4, 2] = 15

Then rotate it by 180 °. The subtraction of the 4 elements causes a structural change. The square at the Sagrada Família is not centrally symmetrical. It has a bipolar structure, i.e. i.e. the sum of the opposing elements is 16 or 17.

Goethe's Hexeneinmaleins

There are many interpretations of the witch's monkey from Goethe's Faust . In addition to the assumption that it is simply nonsense, it was also interpreted as a construction guide for a magic square - an interpretation that is not one hundred percent convincing.

Construction of magic squares

Construction of a magic square

There are various methods for constructing magic squares, which depend on the length of the edge. The simplest method, called the Siamese method or De-la-Loubère method, works for all magic squares with uneven edges (i.e. 3 × 3, 5 × 5, 7 × 7 etc.). You start at the top in the middle with 1 and then fill in the other numbers one after the other according to the following rule:

If the last number written is not a multiple of n, then enter the next number in the field at the top right of the last field filled out. If the last number written is a multiple of n, then enter the next number in the field below the last number written. If you leave the square upwards according to these rules, write the next number at the very bottom in the column to the right of the column in which the last number was written. If you leave the square to the right, write the next number on the far left in the line above the line of the last number written.

Here, the magic square is considered to be periodically repeated; That is, if you go over the top edge (this happens with the first step), you come back in from below, and if you go out on the right, you come back in from the left. Here is a 7 × 7 square constructed according to this rule:

30th	39	48	1	10	19th	28
38	47	7th	9	18th	27	29
46	6th	8th	17th	26th	35	37
5	14th	16	25th	34	36	45
13	15th	24	33	42	44	4th
21st	23	32	41	43	3	12
22nd	31	40	49	2	11	20th

Based on the Siamese method, additional magic squares with double order can be created with the help of the LUX method by John Horton Conway .

Two other methods are for squares with an even edge length, one for all squares whose edge length is divisible by 4, the other for those where the remainder remains 2 when divided by 4.

A playful method for the construction of magic squares with even orders larger than 4 is possible with the help of Medjig solutions. For this you need the pieces of the Medjig puzzle. These are squares distributed in four quadrants, with dots indicating the numbers 0, 1, 2 and 3 in different arrangements. The puzzle has 18 pieces and there are three different arrangements. See the picture below. The goal of the puzzle is to randomly take 9 squares from the assembly and place this sub-assembly in a 3 × 3 square, so that in each row, column and diagonal there is a total of 9 (points).

The construction of a magic square of the order 6 with the help of the Medjig puzzle goes as follows: Make a 3 × 3 Medjig solution, this time you can choose unlimited from the total assembly. Then you take the well-known classic magic square of order 3 and divide all of the squares into four quadrants. Next, fill in the quadrants with the original number and the three derived modulo 9 numbers up to 36, following Medjig's solution. The original field with the number 8 is thus divided into four areas with the numbers , , and , the field with the number 3, 3, 12, 21 and 30, etc .; see example below. ${\displaystyle 8\ (=8+0\cdot 9)}$ ${\displaystyle 17\ (=8+1\cdot 9)}$ ${\displaystyle 26\ (=8+2\cdot 9)}$ ${\displaystyle 35\ (=8+3\cdot 9)}$

8th   8th   3   3   4th   4th   8th   8th   3   3   4th   4th   1   1   5   5   9   9   1   1   5   5   9   9   6th   6th   7th   7th   2   2   6th   6th   7th   7th   2   2

+ 9 *

=

26th   35   3   21st   4th   22nd   17th   8th   30th   12   31   13   28   10   14th   23   27   9   1   19th   5   32   36   18th   33   24   25th   7th   2   20th   6th   15th   34   16   11   29

In the same way one can create 8th order magic squares. First create a 4 × 4 Medjig solution (sum of the points in each row, column, diagonal 12), and then enlarge z. B. Dürer's 4 × 4 square shown above modulo 16 to 64. In general, several sets of Medjig parts are needed to construct magic squares of the order greater than 9 in this way. For order 12, a 3 × 3 Medjig solution can be doubled horizontally and vertically, and then the 6 × 6 square constructed above can be expanded modulo 36 to 144. The same applies to order 16.

Magic squares of size 4 × 4 with the magic number can be constructed using the following scheme, where the variables and stand for any whole number: ${\displaystyle S}$ ${\displaystyle a}$ ${\displaystyle b}$

General scheme a + b a 12a 7a 11a 8a b 2a 5a 10a 3a 3a + b 4a 2a + b 6a 9a

S = 34; a = 1, b = 13 14th 1 12 7th 11 8th 13 2 5 10 3 16 4th 15th 6th 9

S = 88; a = 3, b = 25 28 3 36 21st 33 24 25th 6th 15th 30th 9 34 12 31 18th 27

The magic number is each . Should z. B. be the value 88, subtract an integer multiple of 21, the remainder is then the number . : For example (as shown in the right square) . ${\displaystyle S}$ ${\displaystyle 21a+b}$ ${\displaystyle S}$ ${\displaystyle (=a)}$ ${\displaystyle b}$ ${\displaystyle 88-3\cdot 21=25}$

Magic squares of this type generally do not consist of the numbers 1, 2, 3,…, 16, and if the values ​​are not chosen well , two fields can contain the same number. The magic number is not only contained in the rows, columns and diagonals, but also in the four quadrants, in the four corner fields and in the small square of the four inner fields. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle 21a+b}$

Others

The magic 4 × 4 squares, in which the quadrants also result in the magic sum, can - if one dispenses with the property that each of the numbers from 1 to 16 should appear exactly once - as a linear combination of the following eight generating, mutually congruent Squares are represented:

Square A 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0	Square B 0 1 0 0 0 0 0 1 0 0 1 0 1 0 0 0	Square C 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0	Square D 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1
Square E. 0 0 0 1 1 0 0 0 0 0 1 0 0 1 0 0	Square F 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 1	Square G 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0	Square H. 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0

Note that these eight generating squares are not linearly independent because

${\displaystyle {A}+{D}+{E}+{H}={B}+{C}+{F}+{G},}$

d. that is, there is a nontrivial linear combination (a linear combination whose coefficients are not all = 0) that gives the 0-square. In other words: each of the eight generating squares can be represented as a linear combination of the remaining seven. Seven generating squares are necessary to generate all magic 4 × 4 squares with the additional property "Quadrants"; the vector space of the 4 × 4 magic squares generated by these squares is 7-dimensional in this sense . It is noteworthy that in all eight generating squares A – H, as in Albrecht Dürer's magic square, not only the rows, columns and diagonals always deliver the same sum (1), but also each of the four "quadrants", the four central fields and the four corner fields. This means that all magic squares that we obtain as linear combinations of these generators have this property. The congruence of the generating squares enables z. B. to generate from A by rotation F, E and G and from this D, B, H and C by mirroring.

The magic square from the copper engraving Melencolia I by Albrecht Dürer as a linear combination of the generating squares A – G:

${\displaystyle X=-4\cdot {A}+8\cdot {B}+14\cdot {C}-5\cdot {D}-1\cdot {E}+6\cdot {F}+16\cdot {G}}$

The sum of the coefficients is natural . ${\displaystyle 34=-4+8+14-5-1+6+16}$

The fact that the 4 quadrants also result in the magic sum does not necessarily have to be the case. The following magic square does not have this property and is therefore linearly independent of the squares A – H:

1	2	15th	16
13	14th	3	4th
12	7th	10	5
8th	11	6th	9

If you add this square to 7 of the squares A – H, you get a basis for the 8-dimensional vector space of all magic 4 × 4 squares. The sum of the corners and the four center fields is also the magic sum for this square (as with all magic 4 × 4 squares).

Letter squares

A magic letter square is a brain teaser, where the same words appear in the rows and columns of the square. An example of this is the sator square :

S.	A.	T	O	R.
A.	R.	E.	P	O
T	E.	N	E.	T
O	P	E.	R.	A.
R.	O	T	A.	S.

Number puzzle

Are number puzzles arranged in squares

• Mazara
• Sudoku

Further topics

• Magic Cube , a three-dimensional extension of magic squares
• Magic hexagon , an arrangement of numbers in a honeycomb shape
• Perfectly perfect magic square , magic squares with additional properties of the sub-squares
• Magical sound square
• Magic graph

Supplementary literature

• Jacques Sesiano: Manufacturing process of magic squares from Islamic times. I-III. In: Sudhoff's archive. Volume 64, 1980, No. 2, pp. 187-196; Volume 65, 1981, No. 3, pp. 251-256; Volume 71, 1987, No. 2, pp. 78-89; Volume 79, 1995, No. 2, pp. 192-226.
• Siegmund Günther: Mixed studies on the history of the mathematical sciences. Verlag Teubner Leipzig, 1876, chap. IV, Historical Studies of Magic Squares
• Wolfgang Göbels: Variants of the magic square by Albrecht Dürer. In: Practice of Mathematics (PM) 4/35. Born in 1993, Aulis Verlag

Web links

Commons : Magic Square  - collection of images, videos and audio files

• In-depth articles on magic squares
• Page of the artist Paul Heimbach, Cologne
  • History
• Page no longer available , search in web archives: Dürer's magic square and its meaning in Thomas Mann's Doctor Faustus
• Christoph Pöppe: Noble magic squares. Some magic squares have an internal structure that allows a single magic square to be made into many others. In: Spektrum der Wissenschaft 1. 1996, p. 14 , accessed on February 28, 2012 . 
• Consideration of magic squares with explanations about the sum combinations in the magic square by Albrecht Duerer

Individual evidence

1. ↑ Magic squares. At: mathe-online.at. (PDF).
2. ↑ Hans-Wolfgang Henn, Andreas Filler: Didactics of Analytical Geometry and Linear Algebra, Springer Spectrum, pages 129-134
3. ↑ Eric W. Weisstein : Prime Magic Square . In: MathWorld (English).
4. ↑ ^{a b c d} Correspondence circle MATHEMATICS - LSGM, issue 06/2003, PDF. P. 4.
5. ↑ Martin Gardner : Mathematical Labyrinth: New Problems for the Knobelgemeinde . Vieweg Verlag , Braunschweig / Wiesbaden 1979, ISBN 978-3-528-08402-8 , p. 87 , doi : 10.1007 / 978-3-322-83962-6_9 .
6. ^ Enumeration of magic squares. At: trump.de.
7. ↑ Philos-Spiele, Art-No. 6343.