Pandiagonal magic square

from Wikipedia, the free encyclopedia

A pandiagonal magic square (sometimes also called panmagic or diabolic) is a magic square in which the broken diagonals also add up to the magic sum.

Broken diagonals

The broken diagonals run parallel to the main or secondary diagonals and are viewed cyclically. So if you leave the square at one end, the diagonal continues on the opposite side.

1 8th 13 12
14th 11 2 7th
4th 5 16 9
15th 10 3 6th
1 8th 13 12
14th 11 2 7th
4th 5 16 9
15th 10 3 6th

The following applies to the broken diagonals running upwards

  • 10 + 16 + 7 + 1 = 34
  • 3 + 9 + 14 + 8 = 34
  • 6 + 4 + 11 + 13 = 34

and also for the downward-broken running diagonals

  • 8 + 2 + 9 + 15 = 34
  • 13 + 7 + 4 + 10 = 34
  • 12 + 14 + 5 + 3 = 34

Shifts

The shift is a special exchange operation for magic squares with a pandiagonal property. As a result of the shift, magic squares are converted into one another within a shift cluster. Since the broken diagonals also give the magic sum, any number of lines can be cut off at the top of the square and added again at the bottom. Any number of columns can also be separated from the left edge of the square and added again to the right edge. In all cases a pandiagonal magic square is created again.

Horizontal and vertical shifts in a pandiagonal magic square

By combining the two transformations, any cell of the magic square can be moved to the upper left corner without losing the pandiagonal property.

Any shift in a pandiagonal magic square

Therefore, pandiagonal magic squares, which cannot be converted into one another by any image, are called essentially different .

3x3 pandiagonal magic squares

It is easy to check that there is not a single 3-order pandiagonal square. For higher orders, the exact number is partly known or can be estimated.

4x4 pandiagonal magic squares

There are 48 pandiagonal magic squares in total. 16 magic squares each belong to one of the three displacement clusters. So, all 4th order pandiagonal magic squares can be formed easily.

1 8th 13 12
14th 11 2 7th
4th 5 16 9
15th 10 3 6th
1 12 7th 14th
8th 13 2 11
10 3 16 5
15th 6th 9 4th
1 8th 11 14th
12 13 2 7th
6th 3 16 9
15th 10 5 4th

When shifting pandiagonal magic squares of the 4th order (SG 1) in the shift cluster, there is no change in the internal structure. This is a special property of this structural group. It is recommended to derive this property from the structure of structure group 1.

In the case of pandiagonal magic squares of the 4th order (SG 1), original and complement belong to the same displacement cluster.

The magic sum 34 occurs very frequently in a 4th order pandiagonal square. The following properties are shown using the example of the square on the left:

  • The sum of the numbers in all sixteen 2x2 sub-squares is 34, e.g. B. 1 + 8 + 14 + 11, 8 + 13 + 11 + 2 etc. In this case, these sub-squares can also be viewed cyclically, e.g. B. 12 + 7 + 1 + 14 or 6 + 12 + 15 + 1.
  • The sum of the corners of all 3x3 sub-squares always results in 34, e.g. B. 1 + 13 + 4 + 16 or 8 + 12 + 5 + 9.
  • The diagonally opposite corners of all 3x3 sub-squares always add up to 34. Therefore, there cannot be a symmetrical pandiagonal fourth order square.
  • Each pair of horizontally or vertically neighboring numbers results in a total of 34 with the numbers two rows below and two columns to the right, e.g. B. 1 + 8 + 16 + 9 or 1 + 14 + 16 + 3.

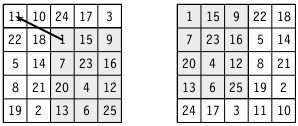
5x5 pandiagonal magic squares

In contrast to order 4, there are also symmetrical pandiagonal squares, since, as in the following example, every number added with its symmetrical number to the center always gives the complement n 2 +1.

1 15th 22nd 8th 19th
23 9 16 5 12
20th 2 13 24 6th
14th 21st 10 17th 3
7th 18th 4th 11 25th

There are a total of 3600 fifth-order pandiagonal squares, of which only 144 are significantly different. A very old pandiagonal square from the Arab world dates from the 11th or 12th century. The special properties of a pandiagonal square were not yet known and were only analyzed by AH Frost in the 19th century.

15th 2 19th 6th 23
16 8th 25th 12 4th
22nd 14th 1 18th 10
3 20th 7th 24 11
9 21st 13 5 17th

6x6 pandiagonal magic squares

There is no sixth-order pandiagonal magic square. The proof was provided by AH Frost as early as 1878. Another elegant proof comes from C. Planck (1919). In general, there is no single-even order n = 4k + 2 with a pandiagonal square.

7x7 pandiagonal magic squares

Pandiagonal magic squares of this order have been studied very intensively by Albert L. Candy. He found that there are 678 222 720 pandiagonal squares, of which 38 102 400 are regular and 640 120 320 are irregular.

1 28 39 9 48 19th 31
46 16 34 5 24 36 14th
27 40 10 43 21st 32 2
17th 29 7th 25th 37 13 47
42 11 44 20th 33 3 22nd
30th 6th 26th 38 8th 49 18th
12 45 15th 35 4th 23 41
1 43 40 32 28 18th 13
24 20th 9 2 47 38 35
46 42 31 26th 16 8th 6th
15th 12 4th 49 39 33 23
41 30th 22nd 19th 11 7th 45
14th 3 48 37 29 27 17th
34 25th 21st 10 5 44 36

8x8 pandiagonal magic squares

The number of 8th order pandiagonal squares is unknown. The following example has been constructed with an algorithm by Portier. It is not only a pandiagonal, but even a cabalistic magic square and thus has the following properties:

  • it's pandiagonal
  • it's bimagic
  • it has trimagic diagonals
  • the entire square can be divided into eight 2x4 rectangles, the numbers of which always add up to 260, e.g. B. 20 + 16 + 39 + 59 + 34 + 62 + 21 + 9 = 260
20th 16 5 25th 54 42 35 63
39 59 50 46 1 29 24 12
34 62 55 43 8th 28 17th 13
21st 9 4th 32 51 47 38 58
11 23 30th 2 45 49 60 40
64 36 41 53 26th 6th 15th 19th
57 37 48 52 31 3 10 22nd
14th 18th 27 7th 44 56 61 33

9x9 pandiagonal magic squares

Pandiagonal squares of an order that are a multiple of 3 have long been considered impossible. The first known example of such a square comes from AH Frost in 1878.

57 80 67 12 8th 22nd 48 44 31
10 9 23 46 45 32 55 81 68
47 43 33 56 79 69 11 7th 24
62 76 66 17th 4th 21st 53 40 30th
18th 5 19th 54 41 28 63 77 64
52 42 29 61 78 65 16 6th 20th
58 75 71 13 3 26th 49 39 35
14th 1 27 50 37 36 59 73 72
51 38 34 60 74 70 15th 2 25th

Higher orders and construction

Higher order pandiagonal squares can be generated using the same algorithms as lower order squares. A distinction is made between procedures for the following orders:

  • odd multiples of 3 (9, 15, 21, ...)
  • odd, but not a multiple of 3 (5, 7, 11, 13, 17, 19, 23, 25, ...)
  • double straight (4, 8, 12, ...)
  • Prime numbers (5, 7, 11, 13, 17, 19, 23, 29, ...)

You can also find options for constructing pandiagonal magic squares online.

Individual evidence

  1. ↑ Clifford A Pickover: The Zen of Magic Squares, Circles, and Stars. Princeton University Press, Princeton 2002, pp. 68-77.
  2. ↑ Enumeration of magic squares (English)
  3. ^ William H. Benson, Oswald Jacoby: New Recreations with Magic Squares. Dover Publications, New York 1976, p. 49.
  4. ↑ Schuyler Cammann: Islamic and Indian Magic Squares (Part I). In: History of Religions. Vol. 8, No. 3, 1969, pp. 181-209.
  5. ↑ a b c A. H. Frost: On the General Properties of Nasik squares. In: The Quarterly Journal of Pure and Applied Mathematics. Vol. 15, 1878, pp. 34-48.
  6. ↑ C. Planck: Pandiagonal Magic squares of Order 6 and 10 with Minimal Numbers. In: The Monist. Vol. 29, 1919, pp. 307-316.
  7. ↑ Albert L. Candy: pandiagonal magic squares of prime order. Self-published, 1940.
  8. ^ Brutus Portier: Le Carré Cabalistique de 8. Librairie Adolphe Jourdan, Alger 1902.
  9. ^ Construction of pandiagonal magic squares

Web links