Frieze group

Frieze or ribbon ornament groups are special groups that are studied in mathematics , more precisely in discrete geometry .

Basic idea

Band ornaments (or friezes ) are patterns that are formed by putting a certain smallest unit (e.g. a pattern or a figure) together again and again along a fixed direction (the so-called frieze direction ). A ribbon ornament group, on the other hand, is clearly seen as the symmetry group of a certain ribbon ornament, but the ribbon ornament is imagined to be extended to infinity in both directions. Ribbon ornaments can have many different shapes and figures, which are difficult to handle mathematically, so that ribbon ornament groups can only be defined mathematically in this way with difficulty.

However, all ribbon ornament groups have one thing in common: Due to its construction, a ribbon ornament is definitely depicted on itself if it is shifted by one unit or by a multiple of this unit along the direction of the frieze. Such shifts or translations ( parallel shifts ) therefore belong to the symmetry group of a ribbon ornament. But they are also the only possible shifts that a

Example of a frieze and most important designations

Band ornament depicts itself, in particular there are no shifts in a direction other than in the frieze direction (or in the opposite direction). The only displacements that can and must appear within a symmetry group of a frieze are displacements by a multiple of a vector , the length of which is equal to the distance between two smallest units and which points in the direction of the frieze. Denoting with such a vector , as is true for any shift of the frieze from the symmetry group: . In other words: all the shifts occurring in the symmetry group of the ribbon ornament belong to the group generated by, in particular the translations of a ribbon ornament group form a cyclic group . This property of frieze symmetry groups is used for the mathematical definition of a band ornament group. ${\ displaystyle v_ {G}}$ ${\ displaystyle \ tau _ {v}}$ ${\ displaystyle \ tau _ {v} = \ tau _ {nv_ {G}} = (\ tau _ {v}) ^ {n}}$ ${\ displaystyle \ tau _ {v_ {G}}}$

Mathematical definition

Frieze group

The translation vector belonging to a generating translation is also called a Fries vector ; it is uniquely determined except for the sign . The straight line is called the direction of the frieze. Since the set of translations of a group consisting of isometries is itself a group, T (G) is also called the translation group of G. It should be pointed out that the n-fold arrangement of the figure denotes and that the following applies: ${\ displaystyle v_ {G}}$ ${\ displaystyle \ mathbb {R} v_ {G}}$ ${\ displaystyle \ tau _ {v} ^ {n}}$ ${\ displaystyle \ tau _ {v}}$ ${\ displaystyle \ tau _ {v} ^ {n} = \ tau _ {nv}}$

Background: If the plane is a discrete group of movements , there are only three possibilities: 1) , and is a point group ; 2) , and is a frieze group; 3) , and is an ornament group . ${\ displaystyle G}$ ${\ displaystyle T (G) = \ {{\ text {Id}} \}}$ ${\ displaystyle G}$ ${\ displaystyle T (G) \ cong \ mathbb {Z}}$ ${\ displaystyle G}$ ${\ displaystyle T (G) \ cong \ mathbb {Z} ^ {2}}$ ${\ displaystyle G}$

Classification of frieze groups

On closer inspection, one finds that there are “so many” frieze groups that do not exist. H. many frieze groups are similar in a certain sense. One thinks of the concept of similarity, which is defined in the next section.

Classification

similarity

The similarity of groups has the properties of an equivalence relation , so that with the definition of the similarity the set of all subgroups is decomposed by disjoint. ${\ displaystyle Iso (E)}$

It turns out that there are only seven types of ribbon ornament groups in terms of similarity. So you choose any band ornament group G, so there is a group H of one of the types described below seven and a bijective affine with . All types are systematically numbered and listed and described in the following list (in the following a generating element of the translation group of G). ${\ displaystyle \ phi}$ ${\ displaystyle G = \ phi H \ phi ^ {- 1}}$ ${\ displaystyle \ tau _ {v_ {G}} =: \ tau _ {G}}$

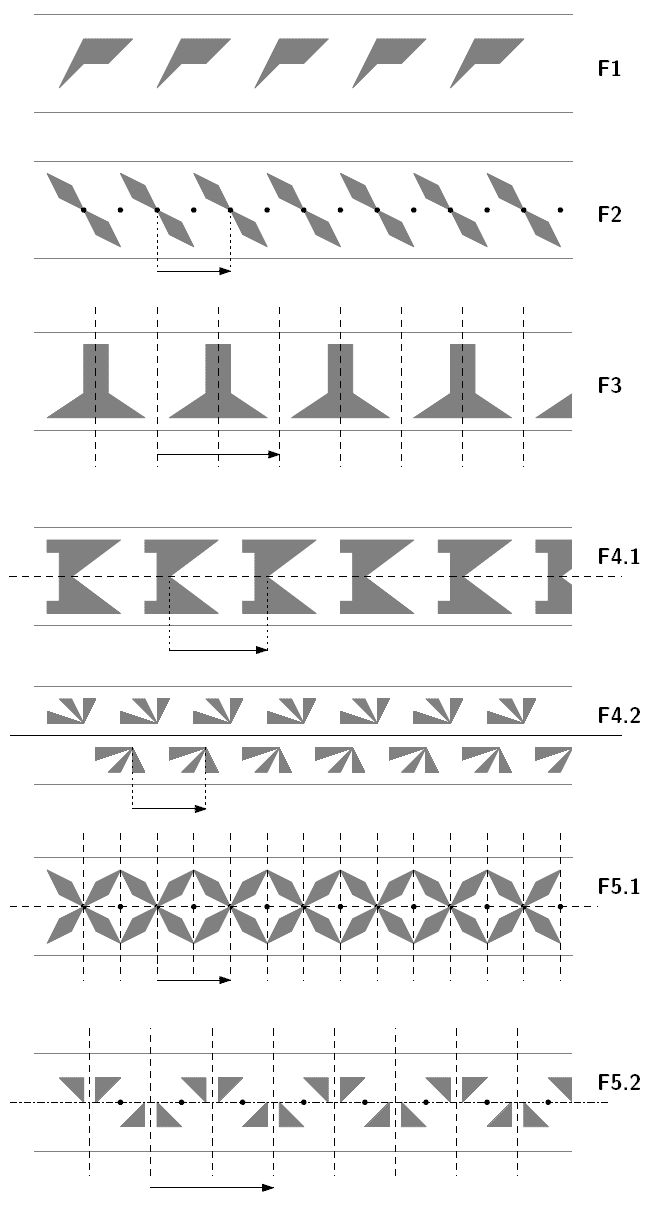
Types of ribbon ornament groups:

F1	A group of type F1 contains only translations of the form . ${\ displaystyle \ tau _ {G} ^ {n}}$
F2	Groups of type F2 only contain translations of the above type as well as point reflections at centers of the form with ${\ displaystyle {\ frac {n} {2}} v_ {G}}$ ${\ displaystyle n \ in \ mathbb {Z}}$
F3	Band ornament groups of this type contain translations as well as reflections on axes perpendicular to the direction of the frieze. The axes run through the points ${\ displaystyle {\ frac {n} {2}} v_ {G}, n \ in \ mathbb {Z}}$
F4.1	Such groups consist of translations and (shear) reflections on an axis parallel to the direction of the frieze. The displacement vectors of these shear reflections are of the shape ${\ displaystyle nv_ {G}, n \ in \ mathbb {Z}}$
F4.2	Groups of type 4.2 contain translations and shear reflections on an axis parallel to the frieze direction with a displacement vector of the shape . ${\ displaystyle {\ frac {1} {2}} v_ {G} + nv_ {G}, n \ in \ mathbb {Z}}$
F5.1	Groups of this type contain the same images as groups of type F4.1 plus the images of type F2 and F3.
F5.2	Contains all the figures described under F2, F3 and F4.2.

Proof of classification (sketch)

The proof of the classification is carried out via the so-called point group S (G) of a frieze group G. The point group of G consists of all linear portions of the images of G: . In the proof one thinks about which point groups are possible and reconstructs possible frieze groups from them. ${\ displaystyle S (G) = \ {L: E \ rightarrow E {\ mbox {linear}} \; | \ exists v \ in E: \ varphi _ {v, L} \ in G \}}$

Since the translation group is cyclic, it contains a translation with the shortest possible translation vector. This is easy to show, because all vectors belonging to translations are of the form if a vector belongs to a generating element of the translation group. Apparently the shortest possible vectors belonging to a translation are. We now consider any element of a frieze group, with ( i.e. with displacement vector v and linear part L). Because of the group properties of G there is with and also in G, but one calculates directly that , is a translation, so its displacement vector must be of the form . Since L is an isometric view and given lengths, is the same length as , must therefore be one of the shortest possible translation vectors, ie . It now adds to an orthogonal basis and considering due to the Isometrieeigenschaften of L that must apply. Using the existence and uniqueness theorem, all possible linear proportions of any image of a ribbon ornament group result. So you can see that there are a total of four possible images, i.e. five possible point groups (namely the group of all images and their subgroups). In order to reconstruct the frieze groups G, one then thinks about which displacement vectors are possible for a mapping from G for each point group. One finds: If a point group contains a reflection on a straight line in the direction of the frieze, two cases must be distinguished: ${\ displaystyle v = nv_ {G}, n \ in \ mathbb {Z}}$ ${\ displaystyle v_ {G}}$ ${\ displaystyle \ pm v_ {G}}$ ${\ displaystyle \ varphi _ {v, L}}$ ${\ displaystyle \ varphi _ {v, L} (x) = v + L (x)}$ ${\ displaystyle \ phi _ {v, L}}$ ${\ displaystyle \ tau _ {v_ {G}}}$ ${\ displaystyle \ varphi _ {v, L} \ tau _ {v_ {G}} \ varphi _ {v, L} ^ {- 1}}$ ${\ displaystyle \ varphi _ {v, L} \ tau _ {v_ {G}} \ varphi _ {v, L} ^ {- 1} = \ tau _ {L (v_ {G})}}$ ${\ displaystyle L (v_ {G})}$ ${\ displaystyle nv_ {G}, n \ in \ mathbb {Z}}$ ${\ displaystyle L (v_ {G})}$ ${\ displaystyle v_ {G}}$ ${\ displaystyle L (v_ {G})}$ ${\ displaystyle L (v_ {G}) = \ pm v_ {G}}$ ${\ displaystyle v_ {G}}$ ${\ displaystyle (v_ {G}, w_ {G})}$ ${\ displaystyle L (w_ {G}) = \ pm w_ {G}}$

The frieze group itself contains a reflection
The frieze group itself contains only shear reflections

This consideration leads to the splitting of cases 4 and 5 into two “sub-cases” 4.1 and 4.2 or 5.1 and 5.2. After one has found all possible group types through the above considerations, one shows explicitly by construction of a suitable map that groups that belong to the same cases are similar to one another. It also proves that groups belonging to different cases cannot be similar to one another.

Examples

Below are some examples of each type of frieze group. The frieze shown has the corresponding frieze group as a symmetry group. The gray elements each belong to the pattern, symmetry elements are drawn in black: dots indicate centers of inversion, dashed lines indicate mirror axes, solid or dash-dotted lines indicate real sliding mirror axes, the arrow indicates one of the two possible frieze vectors.

The following picture shows a frieze of type F5.1 (from a floor carpet):

Variables and dictionary of terms

List of important variables used in the article:

symbol	Explanation
${\ displaystyle \ tau _ {v}}$	A translation, mapping of the form ${\ displaystyle \ tau _ {v} (x) = v + x}$
${\ displaystyle \ tau _ {G}}$	${\ displaystyle = \ tau _ {v_ {G}}}$
${\ displaystyle \ mathbb {R} v}$	The amount ${\ displaystyle \ {kv \| k \ in \ mathbb {R} \}}$
${\ displaystyle v_ {G}}$	Frieze direction
E.	A two-dimensional vector space
${\ displaystyle Iso (E)}$	The set of all isometries of E
${\ displaystyle T (G)}$	The set of all translations of G (translation group)
${\ displaystyle \ phi _ {v, L}}$	Illustration of the shape . v is called the displacement vector, L is the linear component. ${\ displaystyle \ phi _ {v, L} (x) = v + L (x)}$

Ribbon ornaments in art ethnology

Ribbon ornaments are used for decoration in many cultures. For example, all seven frieze groups are among the Incas , but three of the seven frieze groups represent 71% of all known finds. In both the Kingdom of Cuba and the Kingdom of Benin , artisans used all seven frieze groups and twelve of the seventeen ornamental groups, but each culture became different Symmetry groups preferred in terms of numbers.

literature

Erhard Quaisser: Discrete Geometry. Introduction, problems, exercises . Spectrum Academic Publishing House, Heidelberg u. a. 1994, ISBN 3-86025-309-3 .
The actual source of this text is a lecture at the University of Dortmund, for which no public script exists.
Klaus Lamotke : The symmetry groups of the plane ornaments . In: Mathematical semester reports . tape 52 , no. 2 , August 2005, p. 153-174 , doi : 10.1007 / s00591-005-0092-y (section 3).
Harald Scheid , Wolfgang Schwarz: Elements of geometry . 5th edition. Springer Spectrum, Berlin 2017, ISBN 978-3-662-50322-5 , §4.2: Symmetries and ornaments .

Web links

Udo Hebisch: Classical Algebra. September 2009, (attention, different names).

Individual evidence

↑ Corollary 2.3 from Michael Klemm: Symmetries of ornaments and crystals. Springer, Berlin a. a. 1982, ISBN 3-540-11644-3 .
^ Dorothy K. Washburn, Donald W. Crowe: Symmetries of Culture. Theory and Practice of Plane Pattern Analysis. 3rd printing. University of Washington Press, Seattle WA u. a. 1998, ISBN 0-295-97084-7 .

[1] Corollary 2.3 from Michael Klemm: Symmetries of ornaments and crystals. Springer, Berlin a. a. 1982, ISBN 3-540-11644-3 .

[2] Dorothy K. Washburn, Donald W. Crowe: Symmetries of Culture. Theory and Practice of Plane Pattern Analysis. 3rd printing. University of Washington Press, Seattle WA u. a. 1998, ISBN 0-295-97084-7 .