Optical Ilusion
An optical illusion or visual illusion is a perception deception of the sense of sight .
Optical illusions can affect almost all aspects of vision. There are depth illusions, color illusions, geometric illusions, movement illusions and some more. In all of these cases the visual system seems to make incorrect assumptions about the nature of the visual stimulus, as can be demonstrated with the aid of additional senses or by removing the triggering factors.
Optical illusions are examined in perceptual psychology , as conclusions can be drawn from them about the processing of sensory stimuli in the brain. Optical illusions are based on the fact that perception is based on incomplete information. Optical illusions were first systematically produced and analyzed in Gestalt psychology .
Examples
Relativity of Lines

The square in the picture on the left consists of dark and light partial squares arranged like a checkerboard. In some of the dark partial squares the corners are disturbed by small light squares. The impression arises as if the - demonstrably straight - dividing lines between the sub-squares are curved in a wave-like manner. Their brightness and thickness play an important role.
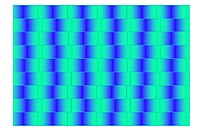
In the example at the top right , the crossbars appear to be wedge-shaped - in truth, all horizontal lines are exactly parallel. This deception was first described in 1874 by Hugo Münsterberg (1863-1916), who found it on an American horse-drawn train ticket, and published in 1894/1897 as The Shifted Chessboard Piece. It is therefore also called the Münsterberg deception . AH Pierce described it in 1898 in the title of a work as Illusion of the Kindergarten Patterns , as it is reminiscent of braided patterns in kindergarten (in Psychological Review 5 (3), 233-253). The recent name comes from Richard L. Gregory , who after a black and white tiled wall in a cafe in the 19th century in the city in 1973 Bristol as Café Wall illusion ( Coffee Bluff ) called. According to McCourt, the café-wall illusion can be explained by a brightness contrast. If the rows of black and white fields are separated by narrow gray lines, then these are perceived as clearly lighter between black fields and darker between light fields. The perception now connects the line segments that appear light with the corners of the light fields and accordingly connects the line segments that appear dark with the corners of the dark fields. These subjective contours are perceived as being inclined to the horizontal and therefore make the rectangles appear wedge-shaped. The effect is not limited to a pattern of alternating black and white tiles, it occurs e.g. B. also with a stepped or continuous shading of the tiles between black and white. The illusion is strongly dependent on the width and the gray value of the dividing line and reaches its maximum when the width of the line is smaller by a factor of two to three than the resolution of the eye (about a minute of arc, i.e. 1/60 degrees of viewing angle). The impression of undulating boundaries can also arise when rows with unequal period lengths are combined. There are also colored versions.
In the fourth example ( bottom left ) the impression arises that the diagonal lines run at an acute angle to one another, but in fact they are exactly straight and parallel. This illusion is also called the tax collector's deception . Compared to humans, pigeons perceive this illusion in exactly the opposite way, they underestimate the angles between the lines.
Relativity of lengths
The example in the picture above on the left shows different variants of the Müller-Lyer illusion .
The two blue, the two pink, the brown and the red as well as the light green and the dark green routes are each the same length.
However, the viewer perceives different lengths.
In the picture at the top right , the red point inside the triangle halves the vertical triangle height. To the viewer, however, the point appears further away from the base of the triangle than from the tip.
The red and blue lines in the trapezoids are of the same length, although the viewer perceives the red line to be longer.
In the picture below on the left , the two red stretches at the wall edges are the same length.
The viewer perceives the right stretch as longer.
This is also a variant of the Müller-Lyer deception .
Relativity of curvatures
In the picture on the left , the curvature strengths of the three arcs seem to decrease from left to right.
However, it can be seen from the corresponding full circles shown in the right part of the picture that all radii are identical.
Thus all arcs have the same curvature.
Relativity of colors
If you look intensively at the green square in the picture for about half a minute and then direct your gaze to the free area next to it, a square in the complementary color red appears as an afterimage .
In 2015, under the keyword #TheDress, the photo of a black and blue colored dress was distributed millions of times on Twitter. Numerous media also showed the picture and reported that most people perceived it as a white and gold-colored dress in the overexposed photo and due to the yellowish light of the surroundings. However, the visual perception of some people corrects the color cast, so that around a fifth of the viewers saw the dress in the actual colors. A minority of people see the dress sometimes in white and gold and sometimes in black and blue. The figure shows how black can be perceived as yellow and blue as white, depending on the color and lighting of the surroundings.
Relativity of brightness
The perception of differences in brightness is very subjective. A hue that is perceived as light in twilight appears dark and different in sunlight. This interpretation is physically correct. The brain draws on this experience when looking at the examples on the left and right.
In the image above left, gray appears lighter in the left area in a dark environment and darker in a lighter environment, although the gray bar has the same gray value everywhere, unless it is viewed at an angle using a flat screen , where there is generally an actual color deviation. In addition, the contour seems to be clearly recognizable at all points, although the basic size of the image has an area several pixels wide in which the gray value of the stripe is identical to that of the background.
The square B on the right in the picture is in the shadow. Following the pattern it has a white square be much brighter than the dark square A . Viewed in absolute terms, however, both squares are equally bright.
The two small gray squares in the image below on the left have exactly the same gray value, although the right square appears significantly lighter than the left square.
This shows in a particularly impressive way how much the viewer's perception depends on the color of the surrounding surfaces.
The Hermann grid
The Hermann grid was introduced by Ludimar Hermann in 1870. As this phenomenon was also noticed by Ewald Hering , it is also known as the Hering grid. At the intersections of the white lines (the "crossings") you can see shadow-like spots, but only where you don't fixate.
Previously it was assumed that the effect was due to lateral inhibition , and this is also represented in current textbooks. However, this theory has now been disproved. If you change the deception only slightly, e.g. B. by sinusoidal bars, the illusion disappears. This property contradicts the theory of lateral escapement.
The scintillation grid
The scintillating grid illusion is an illusion that was discovered by E. and B. Lingelbach and M. Schrauf in 1994. It is often considered a variant of the Hermann grid, but has different properties. Like the Hermann grid, it consists of black squares that are separated from lighter “streets”, but in contrast to the Hermann grid, the streets are not white, but gray and white circular disks are superimposed on the “intersections”. The image must not be too far away or too close for the illusion to occur.
Relativity of size
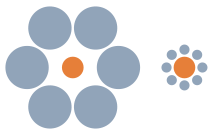
The picture on the left is an example of many similar schematic drawings that confuse human perception. The left orange sphere is smaller than the surrounding blue ones, the right one is the other way around. The transfer of relatively smaller and relatively larger to the two orange balls in direct comparison is wrong. Both orange balls are the same size.
The picture on the right shows a portico and three pairs of sisters. The pair in the foreground appears smaller than the middle pair. The rear pair appears largest. Measuring proves that all three pairs are the same size. The eye provides the image on the retina, but its meaning is only revealed through the processing of the image information in the brain. Although the image is two-dimensional, a path is recognized that runs from front to back and gives the impression of spatial depth. From this it is concluded that objects at the lower edge are nearby and objects in the center of the image are further away.
Image processing in the brain assumes that objects get smaller with increasing distance. So it is not surprising that the woman in the back right in the red coat is extremely small compared to the people on the left in the picture, although she is only further away than the people in the foreground.
The couple in the foreground appear very small because the distance is interpreted as short. If it were actually the same size as the middle pair, it should appear larger in the picture. But since it is exactly the same size as the middle pair in the picture, the brain deduces that the people really have to be smaller. The same goes for the rear pair. Actually, his size should match that of the woman in the red coat. Instead, it's seen more than twice its size. The image processing process records these two people in the background as giants.
The relativity of size is meaningful in the Ponzo illusion . This illusion is also known under the name Railway Lines Illusion , as the figure is reminiscent of railroad tracks. It was developed by the Italian psychologist Mario Ponzo in 1913. Two bars are drawn the same size on two (or more lines that run like straight train tracks). The upper bar looks bigger. The main explanation is the principle of constancy of size . The converging rail lines are interpreted as actually parallel lines that have their vanishing point at great depth. This creates the impression of spatial depth. Due to the spatial interpretation, the upper bar is perceived as further away and should therefore actually be much smaller than the lower bar in order to be perceived as being of the same size. But since the retinal images of both bars are of the same size, the upper bar appears larger.
This optical illusion is used in architecture, photography and film under the term forced perspective to make objects appear larger or more distant in the eye of the beholder.
Relativity of the point of view

Another type of optical illusion arises from the viewer's point of view. For example, you can build objects that only look like an ordinary object, such as a chair or a piano, when viewed from a very specific angle, even though they actually have a completely different, distorted, spatial shape. Or you can build objects that, when viewed from a very specific perspective, simulate spatial figures that are not possible in reality, such as the Penrose triangle opposite .
The “wrong” moon inclination can also be classified under the keyword “relativity of the viewing angle”. This phenomenon can be observed when the moon and sun can be seen in the sky at the same time during the day. One would expect the moon to turn its illuminated side, the sickle, towards the sun, because this is where it receives its light. Instead, the sickle with its axis of symmetry deviates significantly and sometimes even strongly upwards from the expected direction. The sickle looks over the sun, as the adjacent picture shows. Just as unexpectedly, the sickle sometimes points upwards instead of downwards at night despite the sun having set. This phenomenon is an optical illusion, for which there are various explanations, including the fact that the illusion depends on the direction of view.
Different perception of identical images
The illustration on the right shows two photos of an avenue side by side . The viewer gets the impression that the avenue in the right photo rises a little flatter than that in the left photo and that the avenue in the right photo crosses the one in the left photo. In reality, however, the two images were not taken from different angles, but are exactly identical.
Although there are no conclusive explanations for this phenomenon yet , it seems most plausible that our brain interprets the intersection of the two streets in the lower half of the picture as a kind of fork and concludes from this that the two streets cannot run the same, because they would otherwise not cross.
Objects that do not exist
Broken lines of the Ehrenstein illusion
With some sensory impressions, the viewer believes he perceives objects that are not there. An example of this is the broken line pattern shown (left). The viewer thinks he sees white panes at the interfaces.
In the example in the middle, the viewer sees a cube (the Necker cube ). The edges that are not present in the picture are supplemented in the perception. In the case of the Kanizsa triangle (named after Gaetano Kanizsa ) in the picture on the far right, the viewer believes to see a white triangle, although there are only lines and segments of circles in the picture. The imaginary lines ( illusory contours ) are in the literature as " cognitive contours " ( cognitive contours become known).
Similarly, the Martian channels or the face of Mars can be traced back to the endeavor of the perception system to rediscover what is known through pattern recognition.
Ambiguous objects / tilt figures
Tilting figures like the Necker cube are an example of multi-stable perception . Experience determines the position in which the figure is preferably perceived. If you look at the picture for a long time, the Necker cube tilts.
Illusions of movement
There is a long series of optical illusions in which the viewer thinks that parts of the image are moving. Sometimes the head itself has to be moved and sometimes not. The latter variant works best with peripheral vision , which means that the movement can be seen in the areas that are currently not in focus.
An illusion of movement also occurs when looking at a small object in front of an environment that does not provide any clues as to its spatial position. A lonely star in the dark sky seems to be moving.
Static images can also evoke an illusion of movement without moving your head. The cause can be found in repeated patterns within which there are contrasts of varying strength. As a result of the differently fast forwarding of contrasts and brightnesses of different strengths in the periphery of the retina, incorrect processing and thus misinterpretation occurs in the downstream levels of visual processing (keyword: Reichardt detectors ). The "Rotating Snake" is a very good example of this.
Further examples

An Ames room , named after Adelbert Ames, Jr. (1880–1955), is a room with a special geometry in which a series of optical illusions can be realized.
A number of other optical illusions have been known partly since antiquity, partly only in the 19th century and in the recent past. This includes:
- Anamorphosis
- Barber pole illusion
- Delboeuf illusion
- Missing square puzzle
- Fraser spiral
- Hollow-face illusion
- Hybrid image
- Mach strips ( Ernst Mach , 1865)
- Moon illusion
- Mueller-Lyer illusion ( Franz Müller-Lyer , 1889)
- Poggendorff deception ( Johann Christian Poggendorff , 1860)
- Pulfrich effect ( Carl Pulfrich , 1922)
- Converging lines and rays of the sun
- T-figure illusion
- Impossible figure
- Picture puzzle
- Watercolor effect (Baingio Pinna, John S. Werner and Lothar Spillmann , 2003)
Optical illusions in everyday life
These examples show that optical illusions can also occur in everyday life:
- In film , the rapid succession of static individual images creates the illusion of movement. This is the so-called beta movement , which under certain conditions cannot be distinguished from a real movement. However, if the repetition frequency of the images is in a certain relationship to the frequency of a displayed, periodically moving object in television or in the cinema, unreal movements can occur, such as stationary or backward rotating cartwheels. This is known as the stroboscopic effect .
- Under certain landscape conditions, roads that are actually downhill appear to go uphill and vice versa (for example the Electric Brae in Scotland ).
- In illusionist painting, rooms are optically enlarged using the trompe-l'oeil technique.
- The Op-Art uses optical illusions targeted a stylistic device.
Possible explanations for optical illusions
One possible solution to “optical illusions” is the theory of the American Mark Changizi. This speaks of a “look into the future” that the brain does every second. The visual information from the outside world reaches the brain via the retina and the junction of the optic nerves. However, sharp vision is only possible in a small part of the retina. When looking at a visual scene, the eye makes targeted movements (arbitrary saccades). The brain unconsciously fades out the blurred images during eye movement. From the various visual impressions, the impulses reach a part of the thalamus ( Corpus Geniculatum Laterale ) and then into the primary visual center at the occipital pole , the primary visual center. However, there are already feedback loops at this level, so that only about 10% of the nerve fibers come from the eye in the visual center. An essential preprocessing of the signals based on biological parameters and previous experience already takes place at this level. Essentially, the brain itself creates the visual representation of what it sees from relatively weak signals. This mechanism is prone to failure, which makes the optical illusions clear. The brain then further evaluates the information and calculates the expected change for the future, which is important from an evolutionary point of view. For example, vanishing points suggest movement, and the brain recalculates the environment from them. However, since the real position does not change, the optical illusion arises that lines are bent. According to Changizi, this can explain up to 50 deceptions.
Philatelic
On October 10, 2019, the first day of issue, Deutsche Post AG issued two postage stamps in the series Optical Illusions with a face value of 60 (subject: curved lines ) and 80 euro cents (subject: change of perspective ). The designs come from the graphic artist Thomas Steinacker from Bonn.
literature
- Brad Honeycutt: Optical Illusions , ars edition, 2013, 160 pp., ISBN 978-3-8458-0042-4
- Ernst Mach : About the effect of the spatial distribution of the light stimulus on the retina. In: Meeting reports of the mathematical and natural science class of the Imperial Academy of Sciences No. 52, 1865, pp. 303–322.
- Ludimar Hermann : A phenomenon of simultaneous contrasts. In: Pflüger's archive for the entire physiology No. 3, 1870, pp. 13–15.
- William H. Ittelson: The Ames Demonstrations in Perception. Princeton University Press, Princeton 1952.
- Franz C. Müller-Lyer: Optical judgment illusions. In: Archives for Physiology Supplement Volume. 1889, pp. 263-270.
- Hugo Münsterberg: The displaced chess board piece. In: Zeitschrift für Psychologie No. 15, 1897, pp. 184-188.
- Jürg Nänni: Visual Perception. Niggli Verlag, Sulgen / Zurich 2008, ISBN 978-3-7212-0618-0 .
- Nigel Rodgers : Incredible Optical Illusions. Bechtermünz-Verlag, 1999, 228 pages, ISBN 978-3-8289-2318-8 .
- Romana Karla Schuler: Seeing Motion. A History of Visual Perception in Art and Science. De Gruyter, Berlin / Boston 2016, ISBN 978-3-11-042696-0
- Uwe Stoklossa: Eye tricks. Instructions for visual seduction. Hermann Schmidt, Mainz 2005, ISBN 978-3-87439-681-3 .
Web links
- Background information collections
- 48 optical illusions compiled and commented by Michael Bach
- Detailed specialist article on optical illusions
- A. Ray: Illusion of the sense of sight. Lecture (PDF file; 2.1 MB) or as a Flash animation . strahl.info
- 12 fascinating optical illusions that deceive the eye (in English; original title: 12 fascinating optical illusions show how color can trick the eye) . In: The Washington Post . February 27, 2015. Accessed February 27, 2020.
- Working on individual phenomena
Individual evidence
- ^ ME McCourt: Brightness induction and the Café Wall illusion. "Perception" No. 12, 1983. pp. 131-142.
- ^ A. Kitaoka, B. Pinna, G. Breistaff: Contrast polarities determine the direction of Café Wall tilts. "Perception" No. 33, 2004. pp. 11-20.
- ↑ a b Subjective contours triggered by border lines below the resolution limit. at uni-ulm.de
- ^ RL Gregory: Vision with isoluminant color contrast: 1. A projection technique and observations. Perception No. 6, 1977. pp. 113-119.
- ^ S. Watanabe, N. Nakamura, K. Fujita (2011). Pigeons perceive a reversed Zöllner illusion. "Cognition" No. 119 (1). Pp. 137-141.
- ^ Inga Menkhoff: The world of optical illusions , Parragon Books Ltd., pp. 14, 15 and 19.
- ↑ Inga Menkhoff: The world of optical illusions , Parragon Books Ltd., p. 27.
- ↑ see the corresponding article on Wikipedia: The dress
- ^ The Science of Why No One Agrees on the Color of This Dress . In: Wired Magazine , Wired Magazine. Retrieved February 28, 2020.
- ↑ The inside story of the 'white dress, blue dress' drama that divided a planet . In: The Washington Post . Retrieved February 27, 2020.
- ↑ Why that dress looks white and gold: It's overexposed . Retrieved February 27, 2020.
- ↑ Inga Menkhoff: The world of optical illusions , Parragon Books Ltd., p. 50.
- ↑ G. Baumgartner: Indirect size determination of the receptive fields of the retina in humans by means of the Hermann lattice illusion. . In: Pflügers Arch ges Physiol . 272, 1960, pp. 21-22. doi : 10.1007 / BF00680926 .
- ↑ B. Lingelbach, B. Block, B. Hatzky, E. Reisinger: The Hermann grid illusion-retinal or cortical? . In: Perception . 14, No. 1, 1985, p. A7.
- ↑ a b J. Geier, L. Bernáth: Stopping the Hermann grid illusion by simple sine distortion . In: Perception . 33, 2004, p. 53.
- ^ Peter H. Schiller, Christina E. Carvey: The Hermann grid illusion revisited. Archived from the original on December 12, 2011. In: Perception . 34, No. 11, 2005, pp. 1375-1397. doi : 10.1068 / p5447 . Retrieved May 1, 2018.
- ^ J. Geier, L. Bernáth, M. Hudák, L. Séra: Straightness as the main factor of the Hermann grid illusion . In: Perception . 37, No. 5, 2008, pp. 651-665. doi : 10.1068 / p5622 . PMID 18605141 .
- ^ János Geier: Stopping the Hermann grid illusion by sine distortion . 2008.
- ^ Bach, Michael: The Hermann grid illusion: textbook explanation refuted (The Hermann grid illusion: the classic textbook interpretation is obsolete) . In: Ophthalmologist . 106, 2008, pp. 913-917. doi : 10.1007 / s00347-008-1845-5 .
- ↑ a b M. Schrauf, B. Lingelbach, E. Lingelbach, ER Wist: The Hermann Grid and the scintillation effect . In: Perception . 24 Suppl., 1995, pp. 88-89.
- ↑ M. Schrauf, B. Lingelbach, ER Wist: The Scintillating Grid Illusion . In: Vision Research . 37, 1997, pp. 1033-1038.
- ↑ Representation of the "wrong" moon inclination with sketches and geometrical calculations at jimdo.com
- ↑ Astronomical-psychological explanation of the “wrong” moon inclination (PDF; 1.1 MB) at psy-mayer.de
- ^ Bernhard Schölkopf: The moon tilt illusion. ( Memento of December 12, 2011 in the Internet Archive ) Perception magazine No. 27 (10), pp. 1229–1232
- ^ Georg Glaeser , Karlheinz Schott: Geometric Considerations About Seemingly Wrong Tilt of Crescent Moon. “KoG” No. 13, pp. 19–26
- ↑ Based on the article in stern.de of February 7, 2018: Optical illusion: Why these two streets drive the network crazy .
- ^ Richard L. Gregory: Cognitive contours . In: Nature . 238, 1972, pp. 51-52.
- ↑ Chris Frith: How the brain creates the world. Spectrum Scientific publishing house, non-fiction book 2010
- ↑ Heike Le Ker: Optical illusions: Looking into the future tricks the eye. Spiegel Online, 2008 (accessed June 11, 2008)