Samson straight line

Simson straight

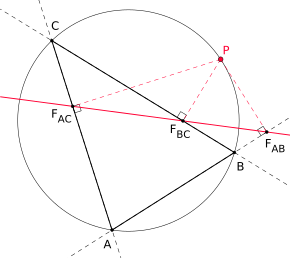
The Samson straight line is an object of triangular geometry . If the base points from a point of precipitated solder on the (possibly extended) sides of a triangle on a common straight line, then this straight line as a Simson line or wallacesche straight line and the point as its pole , respectively. This is exactly the case if lies in the perimeter of . ${\displaystyle P}$ ${\displaystyle \triangle ABC}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle \triangle ABC}$

The Samson straight line is erroneously named after the mathematician Robert Simson (1687–1768), in whose work, however, no work on the Samson straight line can be found. In reality, it was discovered in 1797 by William Wallace (1768–1843).

Other properties

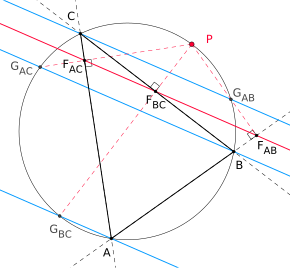
Parallels to the Simson straight line

Simson straight line is parallel to GC Every Simson straight line of a triangle has three particular parallels, which each run through one of the three corner points of the triangle. More precisely, the following theorem applies: A triangle , a point P on its circumference and the associated Simson straight line are given. If G AB is the intersection of the perpendicular from P to AB with the circumference, then the straight line CG is parallel to the Simson straight line. ${\displaystyle \triangle ABC}$

Intersection angle between Simson lines

${\displaystyle 2\alpha =\beta }$ If you look at two different points on the circumference of a triangle, you get two different Simson lines. The angle of intersection of these two Simson straight lines is exactly half the size of the angle that the two points form with the center of the circumference. Let and be two points on the perimeter of with a center . Furthermore, let the intersection angle of the two associated Simson lines and . Then applies . ${\displaystyle P_{1}}$ ${\displaystyle P_{2}}$ ${\displaystyle \triangle ABC}$ ${\displaystyle O}$ ${\displaystyle \alpha }$ ${\displaystyle \beta =\angle P_{1}OP_{2}}$ ${\displaystyle 2\alpha =\beta }$

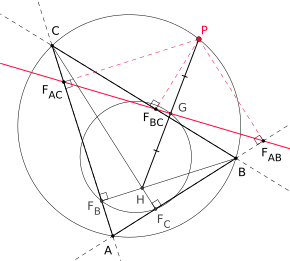
Simson straight line as bisector

${\displaystyle |HD|=|DP|}$ If you connect the vertical intersection of a triangle with a point on the circumference of the triangle, this connecting line is halved by the associated Simson straight line. A triangle , a point on its circumference and the associated Simson straight line are given. H is the orthocenter of , the Simson straight the route cuts in and it is . Also lies on the Feuerbachkreis . ${\displaystyle \triangle ABC}$ ${\displaystyle P}$ ${\displaystyle \triangle ABC}$ ${\displaystyle {\overline {HP}}}$ ${\displaystyle D}$ ${\displaystyle |HG|=|GP|}$ ${\displaystyle G}$

Set of straight lines

Simson lines as tangents of a deltoid If the Samson pole is allowed to move on the circle, the family of Simson straight lines thus created has a deltoid , also referred to as Steiner's hypocycloid , as an envelope curve . ${\displaystyle P}$

Others

If two triangles have the same circumcircle and their associated Simson lines have the same pole, the intersection angle of the two Simson lines is independent of the choice of pole. In other words: For all points on the common circumference of the two triangles, the intersection angle of the two associated Simson lines is the same. ${\displaystyle P}$

proof

Sketch to prove the collinearity of the base points

It is proven: If lies on the perimeter of , the base points lie on a common straight line. One shows that it is true. ${\displaystyle P}$ ${\displaystyle \triangle ABC}$ ${\displaystyle \angle EFP+\angle PFD=180^{\circ }}$

The base points and are above the Thaleskreis . Since circumferential angles (peripheral angles) are equal over the same arc, it follows ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle [PA]}$

${\displaystyle {\begin{aligned}\angle EFP&=90^{\circ }+\angle EFA=90^{\circ }+\angle EPA\\&=90^{\circ }+(90^{\circ }-\angle PAC)=180^{\circ }-\angle PAC\end{aligned}}}$.

On the other hand , a chordal quadrilateral is assumed . The opposite angles and this square therefore complement each other . So overall it results ${\displaystyle PBCA}$ ${\displaystyle \angle PAC}$ ${\displaystyle \angle CBP}$ ${\displaystyle 180^{\circ }}$

${\displaystyle \angle EFP=\angle CBP}$.

The points and are above the Thales circle , so that there is also a quadrilateral tendon. Similar to before you close . Because of it you get ${\displaystyle D}$ ${\displaystyle F}$ ${\displaystyle [PB]}$ ${\displaystyle PBDF}$ ${\displaystyle \angle PFD=\angle DBP}$ ${\displaystyle \angle DBP+\angle CBP=180^{\circ }}$

${\displaystyle {\begin{aligned}\angle PFD&=90^{\circ }-\angle DFB=90^{\circ }-(90^{\circ }-\angle PBD)\\&=\angle PBD=180^{\circ }-\angle CBP\end{aligned}}}$.

So is with

${\displaystyle \angle EFP+\angle PFD=\angle CBP+(180^{\circ }-\angle CBP)=180^{\circ }}$

the claim proved.

Note: The proof given relates to the position of the height base points shown in the sketch. If these are different, the reason must be varied accordingly.

Individual evidence

1. ↑ ^{a b c d e} H. SM Coxeter, SL Greitzer: Simson Lines . §2.5 in Geometry Revisited. In: Math. Assoc. Amer., Washington DC 1967, p. 41.
2. ↑ ^{a b} Eric W. Weisstein : Simson straight line . In: MathWorld (English).

literature

• Max Koecher , Aloys Krieg : level geometry . 3. Edition. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3 , pp. 170-172
• Coxeter, HSM , SL Greitzer: Timeless geometry . Klett, Stuttgart 1983
• Roger A. Johnson: Advanced Euclidean Geometry . Dover 2007, ISBN 978-0-486-46237-0 , pp. 137 ff., 206 ff., 243, 251 (first published in 1929 by the Houghton Mifflin Company (Boston) under the title Modern Geometry )
• Ross Honsberger : Episodes in Nineteenth and Twentieth Century Euclidean Geometry . MAA, 1995, pp. 43-48, 82-83, 121, 128-136

Web links

Commons : Simson-Straight  - collection of pictures, videos and audio files

• Eric W. Weisstein : Simson Straight (Engl.) . In: MathWorld (English).
• Simson Straight on Matroids Math Planet
• Simson straight line (PDF; 48 kB) matheraetsel.de
• Simson Straight (English) cut-the-knot.org