Definitions on the unit circle
Secans and coscans are trigonometric functions . The secant is denoted by, the cosecant by or . The functions get their name from the definition in the unit circle . The function values correspond to the length of secant sections :
sec
(
x
)
{\ displaystyle \ sec (x)}
csc
(
x
)
{\ displaystyle \ csc (x)}
cosec
(
x
)
{\ displaystyle \ operatorname {cosec} (x)}
O
T
¯
=
sec
(
b
)
O
K
¯
=
csc
(
b
)
{\ displaystyle {\ overline {OT}} = \ sec (b) \ qquad \ qquad {\ overline {OK}} = \ csc (b)}
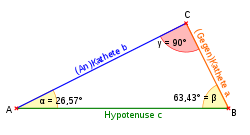
In the right triangle , the secant is the ratio of the hypotenuse to the cathete and thus the reciprocal value function of the cosine function .
The kosekans is the ratio of the hypotenuse to the opposite cathete and thus the reciprocal function of the sine function :
sec
(
α
)
=
l
H
y
l
A.
K
=
c
b
csc
(
α
)
=
l
H
y
l
G
K
=
c
a
{\ displaystyle \ sec (\ alpha) = {\ frac {l _ {\ rm {Hy}}} {l _ {\ rm {AK}}}} = {\ frac {c} {b}} \ qquad \ qquad \ csc (\ alpha) = {\ frac {l _ {\ rm {Hy}}} {l _ {\ rm {GK}}}} = {\ frac {c} {a}}}
sec
(
x
)
=
1
cos
(
x
)
csc
(
x
)
=
1
sin
(
x
)
{\ displaystyle \ sec (x) = {\ frac {1} {\ cos (x)}} \ qquad \ qquad \ csc (x) = {\ frac {1} {\ sin (x)}}}
properties Graph
Graph of the secant function
Graph of the coscan function
Domain of definition
Secans:
-
∞
<
x
<
+
∞
;
x
≠
(
n
+
1
2
)
⋅
π
;
n
∈
Z
{\ displaystyle - \ infty <x <+ \ infty \ quad; \ quad x \ neq \ left (n + {\ frac {1} {2}} \ right) \ cdot \ pi \,; \, n \ in \ mathbb {Z}}
Cosecant:
-
∞
<
x
<
+
∞
;
x
≠
n
⋅
π
;
n
∈
Z
{\ displaystyle - \ infty <x <+ \ infty \ quad; \ quad x \ neq n \ cdot \ pi \; \, n \ in \ mathbb {Z}}
Range of values
-
∞
<
f
(
x
)
≤
-
1
;
1
≤
f
(
x
)
<
+
∞
{\ displaystyle - \ infty <f (x) \ leq -1 \ quad; \ quad 1 \ leq f (x) <+ \ infty}
periodicity
Period length
2
⋅
π
:
f
(
x
+
2
π
)
=
f
(
x
)
{\ displaystyle 2 \ cdot \ pi \,: \, f (x + 2 \ pi) = f (x)}
Symmetries
Secans:
Axial symmetry:
f
(
x
)
=
f
(
-
x
)
{\ displaystyle f (x) = f (-x)}
Cosecant:
Point symmetry:
f
(
-
x
)
=
-
f
(
x
)
{\ displaystyle f (-x) = - f (x)}
Poles
Secans:
x
=
(
n
+
1
2
)
⋅
π
;
n
∈
Z
{\ displaystyle x = \ left (n + {\ frac {1} {2}} \ right) \ cdot \ pi \,; \, n \ in \ mathbb {Z}}
Cosecant:
x
=
n
⋅
π
;
n
∈
Z
{\ displaystyle x = n \ cdot \ pi \; \ quad n \ in \ mathbb {Z}}
Extreme points
Secans:
Minima:
x
=
2
n
⋅
π
;
n
∈
Z
{\ displaystyle x = 2n \ cdot \ pi \,; \, n \ in \ mathbb {Z}}
Maxima:
x
=
(
2
n
-
1
)
⋅
π
;
n
∈
Z
{\ displaystyle x = (2n-1) \ cdot \ pi \; \, n \ in \ mathbb {Z}}
Cosecant:
Minima:
x
=
(
2
n
+
1
2
)
⋅
π
;
n
∈
Z
{\ displaystyle x = \ left (2n + {\ frac {1} {2}} \ right) \ cdot \ pi \; \, n \ in \ mathbb {Z}}
Maxima:
x
=
(
2
n
-
1
2
)
⋅
π
;
n
∈
Z
{\ displaystyle x = \ left (2n - {\ frac {1} {2}} \ right) \ cdot \ pi \; \, n \ in \ mathbb {Z}}
zeropoint Both functions have no zeros.
Asymptotes Both functions have no horizontal asymptotes.
Jump points Both functions have no jump points.
Turning points Both functions have no turning points.
Important functional values Since secant and cosecant are periodic functions with period (corresponds in degree ), it is sufficient to know the function values of the secant for the area and those of the cosecant for the area . Function values outside this range can therefore be due to the periodicity through the context
2
π
{\ displaystyle 2 \ pi}
360
∘
{\ displaystyle 360 ^ {\ circ}}
0
≤
x
≤
2
π
;
x
≠
π
2
,
x
≠
3
π
2
{\ displaystyle 0 \ leq x \ leq 2 \ pi \,; \ quad x \ neq {\ frac {\ pi} {2}}, x \ neq {\ frac {3 \ pi} {2}}}
0
≤
x
≤
2
π
;
x
≠
0
,
x
≠
π
,
x
≠
2
π
{\ displaystyle 0 \ leq x \ leq 2 \ pi \,; \ quad x \ neq 0, x \ neq \ pi, x \ neq 2 \ pi}
sec
(
x
)
=
sec
(
x
+
2
k
π
)
and
csc
(
x
)
=
csc
(
x
+
2
k
π
)
{\ displaystyle \ sec (x) = \ sec (x + 2k \ pi) \ quad {\ text {and}} \ quad \ csc (x) = \ csc (x + 2k \ pi)}
to be determined. In degrees, the relationship is analogous
sec
(
x
)
=
sec
(
x
+
k
⋅
360
∘
)
and
csc
(
x
)
=
csc
(
x
+
k
⋅
360
∘
)
.
{\ displaystyle \ sec (x) = \ sec (x + k \ cdot 360 ^ {\ circ}) \ quad {\ text {and}} \ quad \ csc (x) = \ csc (x + k \ cdot 360 ^ {\ circ}) \ ,.}
Here denotes an integer . The following table lists the important function values of the two trigonometric functions in an easy-to-remember series.
k
∈
Z
{\ displaystyle k \ in \ mathbb {Z}}
Angle (degree)
Radians
Secans
cosecant
0
∘
{\ displaystyle 0 ^ {\ circ}}
0
{\ displaystyle 0}
2
4th
=
1
{\ displaystyle {\ frac {2} {\ sqrt {4}}} = 1}
-
{\ displaystyle -}
30th
∘
{\ displaystyle 30 ^ {\ circ}}
π
6th
{\ displaystyle {\ frac {\ pi} {6}}}
2
3
=
2
3
3
{\ displaystyle {\ frac {2} {\ sqrt {3}}} = {\ frac {2} {3}} {\ sqrt {3}}}
2
1
=
2
{\ displaystyle {\ frac {2} {\ sqrt {1}}} = 2}
45
∘
{\ displaystyle 45 ^ {\ circ}}
π
4th
{\ displaystyle {\ frac {\ pi} {4}}}
2
2
=
2
{\ displaystyle {\ frac {2} {\ sqrt {2}}} = {\ sqrt {2}}}
2
2
=
2
{\ displaystyle {\ frac {2} {\ sqrt {2}}} = {\ sqrt {2}}}
60
∘
{\ displaystyle 60 ^ {\ circ}}
π
3
{\ displaystyle {\ frac {\ pi} {3}}}
2
1
=
2
{\ displaystyle {\ frac {2} {\ sqrt {1}}} = 2}
2
3
=
2
3
3
{\ displaystyle {\ frac {2} {\ sqrt {3}}} = {\ frac {2} {3}} {\ sqrt {3}}}
90
∘
{\ displaystyle 90 ^ {\ circ}}
π
2
{\ displaystyle {\ frac {\ pi} {2}}}
-
{\ displaystyle -}
1
2
4th
=
1
{\ displaystyle {\ frac {1} {2}} {\ sqrt {4}} = 1}
Other important values are:
Angle (degree)
Radians
Secans
cosecant
15th
∘
{\ displaystyle 15 ^ {\ circ}}
π
12
{\ displaystyle {\ tfrac {\ pi} {12}}}
6th
-
2
{\ displaystyle {\ sqrt {6}} - {\ sqrt {2}}}
6th
+
2
{\ displaystyle {\ sqrt {6}} + {\ sqrt {2}}}
18th
∘
{\ displaystyle 18 ^ {\ circ}}
π
10
{\ displaystyle {\ tfrac {\ pi} {10}}}
1
5
50
-
10
5
{\ displaystyle {\ tfrac {1} {5}} {\ sqrt {50-10 {\ sqrt {5}}}}}
1
+
5
{\ displaystyle 1 + {\ sqrt {5}}}
36
∘
{\ displaystyle 36 ^ {\ circ}}
π
5
{\ displaystyle {\ tfrac {\ pi} {5}}}
5
-
1
{\ displaystyle {\ sqrt {5}} - 1}
1
5
50
+
10
5
{\ displaystyle {\ tfrac {1} {5}} {\ sqrt {50 + 10 {\ sqrt {5}}}}}
54
∘
{\ displaystyle 54 ^ {\ circ}}
3
π
10
{\ displaystyle {\ tfrac {3 \ pi} {10}}}
1
5
50
+
10
5
{\ displaystyle {\ tfrac {1} {5}} {\ sqrt {50 + 10 {\ sqrt {5}}}}}
5
-
1
{\ displaystyle {\ sqrt {5}} - 1}
72
∘
{\ displaystyle 72 ^ {\ circ}}
2
π
5
{\ displaystyle {\ tfrac {2 \ pi} {5}}}
1
+
5
{\ displaystyle 1 + {\ sqrt {5}}}
1
5
50
-
10
5
{\ displaystyle {\ tfrac {1} {5}} {\ sqrt {50-10 {\ sqrt {5}}}}}
75
∘
{\ displaystyle 75 ^ {\ circ}}
5
π
12
{\ displaystyle {\ tfrac {5 \ pi} {12}}}
6th
+
2
{\ displaystyle {\ sqrt {6}} + {\ sqrt {2}}}
6th
-
2
{\ displaystyle {\ sqrt {6}} - {\ sqrt {2}}}
180
∘
{\ displaystyle 180 ^ {\ circ}}
π
{\ displaystyle \ pi}
-
1
{\ displaystyle -1}
-
{\ displaystyle -}
270
∘
{\ displaystyle 270 ^ {\ circ}}
3
π
2
{\ displaystyle {\ frac {3 \ pi} {2}}}
-
{\ displaystyle -}
-
1
{\ displaystyle -1}
360
∘
{\ displaystyle 360 ^ {\ circ}}
2
π
{\ displaystyle 2 \ pi}
1
{\ displaystyle 1}
-
{\ displaystyle -}
Evidence Sketches:
sec
(
45
∘
)
=
csc
(
45
∘
)
=
2
{\ displaystyle \ sec (45 ^ {\ circ}) = \ csc (45 ^ {\ circ}) = {\ sqrt {2}}}
right triangle in the unit circle (with hypotenuse 1) is then isosceles , and according to Pythagoras applies .
1
2
+
1
2
=
x
2
⇒
x
=
2
{\ displaystyle 1 ^ {2} + 1 ^ {2} = x ^ {2} \ Rightarrow x = {\ sqrt {2}}}
sec
(
60
∘
)
=
csc
(
30th
∘
)
=
2
{\ displaystyle \ sec (60 ^ {\ circ}) = \ csc (30 ^ {\ circ}) = 2}
opposite cathetus .
x
{\ displaystyle x}
sec
(
30th
∘
)
=
csc
(
60
∘
)
=
2
3
3
{\ displaystyle \ sec (30 ^ {\ circ}) = \ csc (60 ^ {\ circ}) = {\ tfrac {2} {3}} {\ sqrt {3}}}
sin
(
30th
∘
)
=
1
2
{\ displaystyle \ sin (30 ^ {\ circ}) = {\ tfrac {1} {2}}}
(
1
x
)
2
+
(
1
2
)
2
=
1
2
⇒
1
x
2
=
3
4th
⇒
x
2
=
4th
3
⇒
x
=
2
3
3
{\ displaystyle ({\ tfrac {1} {x}}) ^ {2} + \ left ({\ tfrac {1} {2}} \ right) ^ {2} = 1 ^ {2} \ \ Rightarrow \ {\ tfrac {1} {x ^ {2}}} = {\ tfrac {3} {4}} \ \ Rightarrow \ x ^ {2} = {\ tfrac {4} {3}} \ \ Rightarrow \ x = {\ tfrac {2} {3}} {\ sqrt {3}}}
sec
(
72
∘
)
=
csc
(
18th
∘
)
=
1
1
4th
(
5
-
1
)
=
1
+
5
{\ displaystyle \ sec (72 ^ {\ circ}) = \ csc (18 ^ {\ circ}) = {\ frac {1} {{\ tfrac {1} {4}} ({\ sqrt {5}} -1)}} = 1 + {\ sqrt {5}}}
golden section occurs in the pentagram , where the halved angle in the tips is 18 °.
sec
(
36
∘
)
=
csc
(
54
∘
)
=
1
1
4th
(
1
+
5
)
=
5
-
1
{\ displaystyle \ sec (36 ^ {\ circ}) = \ csc (54 ^ {\ circ}) = {\ frac {1} {{\ tfrac {1} {4}} (1 + {\ sqrt {5 }})}} = {\ sqrt {5}} - 1}
golden ratio occurs in the regular pentagon , where the halved interior angle is equal to 54 °.
sec
(
75
∘
)
=
csc
(
15th
∘
)
{\ displaystyle \ sec (75 ^ {\ circ}) = \ csc (15 ^ {\ circ})}
half-angle formulas for sine and cosine.
sec
(
15th
∘
)
=
csc
(
75
∘
)
{\ displaystyle \ sec (15 ^ {\ circ}) = \ csc (75 ^ {\ circ})}
Further function values that can be represented with square roots See also: Sine and Cosine: Further function values that can be specified with square roots
Because of secant each of the reciprocal is the cosine and cosecant is the reciprocal of sine, can the function values and if and with square roots represent when the for and is possible. In general, the four basic arithmetic operations and square roots can be used explicitly and precisely when the angle can be constructed with a compass and ruler , especially if it is of the shape
sec
(
x
)
{\ displaystyle \ sec (x)}
sec
(
x
)
{\ displaystyle \ sec (x)}
sin
(
x
)
{\ displaystyle \ sin (x)}
cos
(
x
)
{\ displaystyle \ cos (x)}
csc
α
{\ displaystyle \ csc \ alpha \;}
sec
α
{\ displaystyle \ sec \ alpha \;}
α
{\ displaystyle \ alpha \;}
α
{\ displaystyle \ alpha \;}
α
=
k
360
∘
2
n
p
1
...
p
r
{\ displaystyle \ alpha = k {\ frac {360 ^ {\ circ}} {2 ^ {n} p_ {1} \ dots p_ {r}}}}
is, where , and which are prime numbers for Fermatsche .
k
∈
Z
{\ displaystyle k \ in \ mathbb {Z} \;}
n
∈
N
0
{\ displaystyle n \ in \ mathbb {N} _ {0} \;}
p
i
{\ displaystyle p_ {i} \;}
i
=
1
,
...
,
r
{\ displaystyle i = 1, \ dots, r \;}
Inverse functions Secans:
On half a period length, e.g. B. the function is reversible ( arc secans ):
x
∈
[
0
,
π
]
{\ displaystyle x \ in [0, \ pi]}
x
=
arcsec
(
y
)
{\ displaystyle x = \ operatorname {arcsec} (y)}
cosecant
On half a period length, e.g. B. the function is reversible ( arccosecans ):
x
∈
[
-
π
2
,
π
2
]
{\ displaystyle x \ in \ left [- {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right]}
x
=
arccsc
(
y
)
{\ displaystyle x = \ operatorname {arccsc} (y)}
Series development Secans:
sec
(
x
)
=
4th
π
∑
k
=
0
∞
(
-
1
)
k
(
2
k
+
1
)
(
2
k
+
1
)
2
π
2
-
4th
x
2
{\ displaystyle \ sec (x) = 4 \ pi \, \ sum _ {k = 0} ^ {\ infty} {\ frac {(-1) ^ {k} (2k + 1)} {(2k + 1 ) ^ {2} \ pi ^ {2} -4x ^ {2}}}}
Cosecant:
csc
(
x
)
=
1
x
-
2
x
∑
k
=
1
∞
(
-
1
)
k
k
2
π
2
-
x
2
=
∑
k
=
-
∞
∞
(
-
1
)
k
x
x
2
-
k
2
π
2
{\ displaystyle \ csc (x) = {\ frac {1} {x}} - 2x \, \ sum _ {k = 1} ^ {\ infty} {\ frac {(-1) ^ {k}} { k ^ {2} \ pi ^ {2} -x ^ {2}}} = \ sum _ {k = - \ infty} ^ {\ infty} {\ frac {(-1) ^ {k} \, x } {x ^ {2} -k ^ {2} \ pi ^ {2}}}}
Derivation Secans:
d
d
x
sec
(
x
)
=
d
d
x
1
cos
(
x
)
=
+
sin
(
x
)
cos
2
(
x
)
=
+
sec
(
x
)
⋅
tan
(
x
)
=
+
sec
2
(
x
)
csc
(
x
)
{\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ sec (x) = {\ frac {\ mathrm {d}} {\ mathrm {d} x}} {\ frac {\ mathrm {1}} {\ cos (x)}} = {\ frac {+ \ sin (x)} {\ cos ^ {2} (x)}} = + \ sec (x) \ cdot \ tan (x) = + {\ frac {\ sec ^ {2} (x)} {\ csc (x)}}}
cosecant
d
d
x
csc
(
x
)
=
d
d
x
1
sin
(
x
)
=
-
cos
(
x
)
sin
2
(
x
)
=
-
csc
(
x
)
⋅
cot
(
x
)
=
-
csc
2
(
x
)
sec
(
x
)
{\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ csc (x) = {\ frac {\ mathrm {d}} {\ mathrm {d} x}} {\ frac {\ mathrm {1}} {\ sin (x)}} = {\ frac {- \ cos (x)} {\ sin ^ {2} (x)}} = - \ csc (x) \ cdot \ cot (x) = - {\ frac {\ csc ^ {2} (x)} {\ sec (x)}}}
integral Secans:
∫
sec
(
x
)
d
x
=
ln
|
1
+
sin
(
x
)
cos
(
x
)
|
+
C.
=
ln
|
sec
(
x
)
+
tan
(
x
)
|
+
C.
=
ln
|
tan
(
x
2
+
π
4th
)
|
+
C.
=
1
2
ln
(
1
+
sin
x
1
-
sin
x
)
+
C.
{\ displaystyle \ int \ sec (x) \, \ mathrm {d} x = \ ln \ left | {\ frac {1+ \ sin (x)} {\ cos (x)}} \ right | + C = \ ln {\ Big |} \ sec (x) + \ tan (x) {\ Big |} + C = \ ln \ left | \ tan \ left ({\ frac {x} {2}} + {\ frac {\ pi} {4}} \ right) \ right | + C = {\ frac {1} {2}} \ ln \ left ({\ frac {1+ \ sin x} {1- \ sin x}} \ right) + C}
cosecant
∫
csc
(
x
)
d
x
=
ln
|
sin
(
x
)
1
+
cos
(
x
)
|
+
C.
=
ln
|
tan
(
x
2
)
|
+
C.
{\ displaystyle \ int \ csc (x) \, \ mathrm {d} x = \ ln \ left | {\ frac {\ sin (x)} {1+ \ cos (x)}} \ right | + C = \ ln \ left | \ tan \ left ({\ frac {x} {2}} \ right) \ right | + C}
Complex argument
sec
(
x
+
i
⋅
y
)
=
2
cos
(
x
)
cosh
(
y
)
cos
(
2
x
)
+
cosh
(
2
y
)
+
i
2
sin
(
x
)
sinh
(
y
)
cos
(
2
x
)
+
cosh
(
2
y
)
{\ displaystyle \ sec (x + \ mathrm {i} \! \ cdot \! y) = {\ frac {2 \ cos (x) \ cosh (y)} {\ cos (2x) + \ cosh (2y)} } + \ mathrm {i} \; {\ frac {2 \ sin (x) \ sinh (y)} {\ cos (2x) + \ cosh (2y)}}}
x
,
y
∈
R.
{\ displaystyle x, y \ in \ mathbb {R}}
csc
(
x
+
i
⋅
y
)
=
-
2
sin
(
x
)
cosh
(
y
)
cos
(
2
x
)
-
cosh
(
2
y
)
+
i
2
cos
(
x
)
sinh
(
y
)
cos
(
2
x
)
-
cosh
(
2
y
)
{\ displaystyle \ csc (x + \ mathrm {i} \! \ cdot \! y) = {\ frac {-2 \ sin (x) \ cosh (y)} {\ cos (2x) - \ cosh (2y) }} + \ mathrm {i} \; {\ frac {2 \ cos (x) \ sinh (y)} {\ cos (2x) - \ cosh (2y)}}}
x
,
y
∈
R.
{\ displaystyle x, y \ in \ mathbb {R}}
Use for numerical calculations - historical significance
Before electronic calculating machines were ubiquitous, tables were used for the trigonometric functions, mostly in printed books. Multiplying by such a function value from a table was more convenient and practical than dividing by such a value (this also applies to non-increasing root values, etc.); If there is a sine or cosine in the denominator in a formula, it is convenient to write the corresponding cosecant or secant values in the numerator instead of these values.
In the age of generally available electronic pocket calculators, this argument is only of historical significance; Secans and cosecans are no longer mentioned in the newer formula collections and are also not implemented as functions (with their own key) in the computers. For this purpose, these functions have simply become superfluous; they solved a problem that no longer exists.
See also Web links Individual evidence
^ Konstantin A. Semendjajew: Taschenbuch der Mathematik ISBN 3-8171-2007-9 , pp. 1220 ( limited preview in Google Book search).
↑ George Hoever: Higher Mathematics compact . Springer Spectrum, Berlin Heidelberg 2014, ISBN 978-3-662-43994-4 ( limited preview in Google book search).
^ Emil Artin : Galois theory. Verlag Harri Deutsch, Zurich 1973, ISBN 3-87144-167-8 , p. 85.
<img src="https://de.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">

























































































![x \ in [0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/49dc087a4edaa359c2dbf3c9064e1370e6782934)

![x \ in \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1456d52196a1482372d7760aa863f111d53aa824)









