Orthoptic curve

The orthoptic curve ( Greek ορθοπτική , straight vision ' ) of a plane curve is in mathematics the geometric location of all points of intersection of orthogonal tangents of the curve . ${\displaystyle k}$ ${\displaystyle k}$

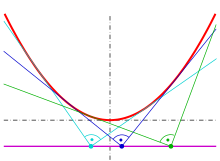
Parabola with an orthoptic curve (purple straight line).

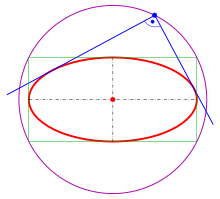
Ellipse with orthoptic curve (purple circle)

Hyperbola with orthoptic curve (purple circle)

Examples: The orthoptic curve

1. a parabola is its guideline (proof: see below ),
2. an ellipse is the circle (see below ), ${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$ ${\displaystyle x^{2}+y^{2}=a^{2}+b^{2}}$
3. of a hyperbola is the circle (in this case there are no orthogonal tangents, see below ), ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\,a>b,}$ ${\displaystyle x^{2}+y^{2}=a^{2}-b^{2}}$ ${\displaystyle a\leq b}$
4. of an astroid is the 4-leaf rosette (quadrifolium) with the equation (in polar coordinates) ${\displaystyle x^{2/3}+y^{2/3}=1}$

   ${\displaystyle r={\tfrac {1}{\sqrt {2}}}\cos(2\varphi ),\ 0\leq \varphi <2\pi ,}$(see below ).

Generalizations:

1. An isoptic curve of a plane curve is the geometric location of all intersection points of tangents of the curve that intersect at a fixed angle (see below ). ${\displaystyle k}$ ${\displaystyle k,}$
2. An isoptic curve of two plane curves is the geometric location of all points of intersection of tangents of the curves that intersect at a fixed angle . ${\displaystyle k_{1},k_{2}}$ ${\displaystyle k_{1},k_{2}}$
3. The Thales circle over a segment can be understood as an orthoptic curve of two circles degenerated to the points . ${\displaystyle {\overline {P_{1}P_{2}}}}$ ${\displaystyle P_{1},P_{2}}$

Note: In ophthalmology there are the similar terms orthoptics and orthoptist .

Orthoptic curve of a parabola

Any parabola can be described by an equation through a suitable displacement and rotation in a Cartesian coordinate system . The slope in a parabolic point is . If you replace in the variable with , you get a parametric representation of the parabola with the slope as parameter: The tangent in a parabola point has the equation with the still unknown -section , which can be determined by inserting the coordinates of the parabola point. For any point of such a tangent one obtains the quadratic equation for the slope ${\displaystyle y=ax^{2}}$ ${\displaystyle (x,ax^{2})}$ ${\displaystyle m=2ax}$ ${\displaystyle (x,ax^{2})}$ ${\displaystyle x}$ ${\displaystyle x={\tfrac {m}{2a}}}$ ${\displaystyle \ ({\tfrac {m}{2a}},{\tfrac {m^{2}}{4a}})\;.}$ ${\displaystyle y=mx+n}$ ${\displaystyle y}$ ${\displaystyle n}$ ${\displaystyle \ y=mx-{\tfrac {m^{2}}{4a}}\;.}$ ${\displaystyle (x,y)=(x_{0},y_{0})}$ ${\displaystyle m}$

${\displaystyle y_{0}=mx_{0}-{\frac {m^{2}}{4a}}\ \leftrightarrow \ \quad m^{2}-4ax_{0}\;m+4ay_{0}=0\;,}$

whose solutions are the slopes of the two tangents through . According to Vieta's theorem, the absolute term of this equation is equal to the product of its solutions, which must be equal to −1 because of the assumed orthogonality of the tangents: ${\displaystyle m_{1},m_{2}}$ ${\displaystyle (x_{0},y_{0})}$

${\displaystyle m_{1}m_{2}=4ay_{0}=-1}$

The last equation is to

${\displaystyle y_{0}=-{\frac {1}{4a}}}$

equivalent to. It is the equation of the guideline of the parabola.

Orthoptic curve of an ellipse or hyperbola

ellipse

Let the considered ellipse. ${\displaystyle \;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;}$

(1) The vertical tangents through the main vertices intersect the horizontal tangents through the secondary vertices in the points . These four points of intersection lie on a circle around the coordinate origin with a radius . ${\displaystyle E}$ ${\displaystyle (\pm a,0)}$ ${\displaystyle (0,\pm b)}$ ${\displaystyle (\pm a,\pm b)}$ ${\displaystyle {\sqrt {a^{2}+b^{2}}}}$

(2) Except for the main vertex, every point of the ellipse is the point of contact of a tangent with the main shape . Solving the tangent equation (see ellipse ) results in ${\displaystyle (u,v)}$ ${\displaystyle E}$ ${\displaystyle y=mx+n}$ ${\displaystyle {\frac {u}{a^{2}}}x+{\frac {v}{b^{2}}}y=1}$ ${\displaystyle y}$

${\displaystyle m=-{\frac {b^{2}u}{a^{2}v}}}$and . ${\displaystyle n={\frac {b^{2}}{v}}}$

Because of the point symmetry to the coordinate origin, there are two parallel tangents for every slope , the main forms of which differ precisely in the sign of . For one pair each is only dependent on, and the position of on the ellipse enables a coordinate-free representation: ${\displaystyle m}$ ${\displaystyle t_{1,2}}$ ${\displaystyle n}$ ${\displaystyle t_{1,2}}$ ${\displaystyle n^{2}}$ ${\displaystyle m}$ ${\displaystyle (u,v)}$

${\displaystyle n^{2}\cdot 1={\frac {b^{4}}{v^{2}}}\cdot ({\frac {u^{2}}{a^{2}}}+{\frac {v^{2}}{b^{2}}})=(\pm {\frac {b^{2}u}{av}})^{2}+b^{2}=m^{2}a^{2}+b^{2}}$

For the general main form of a non-perpendicular tangent, this results in : ${\displaystyle E}$

${\displaystyle y=m\;x\;\pm {\sqrt {m^{2}a^{2}+b^{2}}}}$

For any point on such a tangent, solving the functional equation for yields the quadratic equation ${\displaystyle (x,y)=(x_{0},y_{0})}$ ${\displaystyle m}$

${\displaystyle m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0,}$

whose solutions are the slopes of the two tangents through . According to Vieta's theorem, the absolute term of this equation is equal to the product of its solutions. Except for those considered in (1), two tangents intersect with the slope product of orthogonal straight lines in orthogonal if and only if ${\displaystyle m_{1},m_{2}}$ ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle (x_{0},y_{0})}$

${\displaystyle {\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=m_{1}m_{2}=-1}$

or equivalent

${\displaystyle x_{0}^{2}+y_{0}^{2}=a^{2}+b^{2}}$.

(3) With (1) and (2) the following generally applies:

• The points of intersection of orthogonal tangents lie on a circle around the origin with the radius this is the orthoptic curve of the ellipse . Equivalent to: ${\displaystyle {\sqrt {a^{2}+b^{2}}};}$ ${\displaystyle E}$
• From any point on the orthoptic circle, the ellipse appears at an opening angle of ${\displaystyle 90^{\circ }.}$

hyperbole

The ellipse case can be taken almost literally for the hyperbolic case. The only necessary changes are: 1) replace with and 2) restrict with . This gives: ${\displaystyle b^{2}}$ ${\displaystyle -b^{2}}$ ${\displaystyle m}$ ${\displaystyle |m|>b/a}$

• The points of intersection of orthogonal tangents are at a fixed circle of radius It must be. ${\displaystyle {\sqrt {a^{2}-b^{2}}}.}$ ${\displaystyle a>b}$

Orthoptic curve of an astroid

Orthoptic curve (purple) of an astroid

An astroid can be identified through the parametric representation

${\displaystyle {\vec {c}}(t)=(\cos ^{3}t,\sin ^{3}t),\;0\leq t<2\pi }$

describe. With the help of the condition you can determine the distance (in the parameter area) at which a tangent that is too orthogonal is located. Regardless of the parameter, it follows that it applies. The equations of the (orthogonal) tangents in points and are: ${\displaystyle {\vec {\dot {c}}}(t)\cdot {\vec {\dot {c}}}(t+\alpha )=0}$ ${\displaystyle \alpha }$ ${\displaystyle {\vec {\dot {c}}}(t)}$ ${\displaystyle t}$ ${\displaystyle \alpha =\pm {\tfrac {\pi }{2}}}$ ${\displaystyle {\vec {c}}(t)}$ ${\displaystyle {\vec {c}}(t+{\tfrac {\pi }{2}})}$

${\displaystyle y=-\tan t(x-\cos ^{3}t)+\sin ^{3}t}$

${\displaystyle y={\tfrac {1}{\tan t}}(x+\sin ^{3}t)+\cos ^{3}t}$

Their point of intersection has the coordinates:

${\displaystyle x=\sin t\cos t(\sin t-\cos t)}$

${\displaystyle y=\sin t\cos t(\sin t+\cos t)}$

This is at the same time a parameter representation of the associated orthoptic curve. If the parameter is eliminated , the implicit representation is obtained ${\displaystyle t,}$

${\displaystyle 2(x^{2}+y^{2})^{3}-(x^{2}-y^{2})^{2}=0.}$

If we introduce the new parameter , we get (proof: addition theorems ): ${\displaystyle \varphi =t-{\tfrac {5}{4}}\pi }$

${\displaystyle x={\tfrac {1}{\sqrt {2}}}\cos(2\varphi )\,\cos \varphi }$

${\displaystyle y={\tfrac {1}{\sqrt {2}}}\cos(2\varphi )\,\sin \varphi }$

The simple polar representation can be used here

${\displaystyle r={\frac {1}{\sqrt {2}}}\cos(2\varphi ),\ 0\leq \varphi <2\pi }$

read off.

• The orthoptic curve of an astroid is a four-leaf (quadrifolium).

Isoptic curves of parabola, ellipse and hyperbola

Isoptic curves (purple) of a parabola for the angles 80 and 100 degrees

Isoptic curves (purple) of an ellipse for angles 80 and 100 degrees

Isoptic curves (purple) of a hyperbola for the angles 80 and 100 degrees

In the following, the isoptic curves for an intersection angle are specified and referred to as -isoptic curves. For the evidence see p. below . ${\displaystyle \alpha \neq 90^{\circ }}$ ${\displaystyle \alpha }$

Isoptic curve equations

parabola

The -isoptic curves of the parabola with the equation are the branches of the hyperbola ${\displaystyle \alpha }$ ${\displaystyle y=ax^{2}}$

${\displaystyle x^{2}-\tan ^{2}\alpha \;(y+{\frac {1}{4a}})^{2}-{\frac {y}{a}}=0.}$

The two branches of the hyperbola provide the isoptic curves for the two angles (see picture). ${\displaystyle \alpha ,180^{\circ }-\alpha }$

ellipse

The -isoptic curves of the ellipse with the equation are parts of the curve of the 4th degree ${\displaystyle \alpha }$ ${\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1}$

${\displaystyle \tan ^{2}\alpha \;(x^{2}+y^{2}-a^{2}-b^{2})^{2}=4(a^{2}y^{2}+b^{2}x^{2}-a^{2}b^{2})}$ (see picture).

hyperbole

The isoptic curves of the hyperbola with the equation are parts of the curve of the fourth degree ${\displaystyle \alpha }$ ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$

${\displaystyle \tan ^{2}\alpha \;(x^{2}+y^{2}-a^{2}+b^{2})^{2}=4(a^{2}y^{2}-b^{2}x^{2}+a^{2}b^{2}).}$

The isoptic curves of the ellipse and hyperbola are spiral curves .

proofs

parabola

A parabola can be parameterized by the tangent slope : ${\displaystyle y=ax^{2}}$ ${\displaystyle m=2ax}$

${\displaystyle {\vec {c}}(m)=\left({\frac {m}{2a}},{\frac {m^{2}}{4a}}\right),\,m\in \mathbb {R} }$

The tangent to the slope has the equation ${\displaystyle m}$

${\displaystyle y=mx-{\frac {m^{2}}{4a}}.}$

A point lies on the tangent when ${\displaystyle (x_{0},y_{0})}$

${\displaystyle y_{0}=mx_{0}-{\frac {m^{2}}{4a}}}$

holds, that is, the slopes of the two tangents by satisfy the quadratic equation ${\displaystyle m_{1},m_{2}}$ ${\displaystyle (x_{0},y_{0})}$

${\displaystyle m^{2}-4ax_{0}m+4ay_{0}=0.}$

So that the intersection angle of the two tangents is or must be ${\displaystyle \alpha }$ ${\displaystyle 180^{\circ }-\alpha }$

${\displaystyle \tan ^{2}\alpha =\left({\frac {m_{1}-m_{2}}{1+m_{1}m_{2}}}\right)^{2}}$

be valid. If one solves the quadratic equation for inserting the two solutions into the last equation, the equation is obtained after removing the denominators that contain them ${\displaystyle m,}$ ${\displaystyle m_{1},m_{2}}$ ${\displaystyle x_{0},y_{0}}$

${\displaystyle x_{0}^{2}-\tan ^{2}\alpha \;\left(y_{0}+{\frac {1}{4a}}\right)^{2}-{\frac {y_{0}}{a}}=0.}$

This is the hyperbola equation above, the branches of which are the two isoptic curves of the parabola to the angles and . ${\displaystyle \alpha }$ ${\displaystyle 180^{\circ }-\alpha }$

ellipse

For an ellipse , the approach for the orthoptic curve up to the quadratic equation can be used ${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

${\displaystyle m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0}$

take over. Here, as in the parabola case, one has to solve the quadratic equation, insert the solutions into the equation and eliminate the denominators. The asserted equation of the 4th degree results: ${\displaystyle m_{1},m_{2}}$ ${\displaystyle \tan ^{2}\alpha =({\tfrac {m_{1}-m_{2}}{1+m_{1}m_{2}}})^{2}}$

${\displaystyle \tan ^{2}\alpha \left(x_{0}^{2}+y_{0}^{2}-a^{2}-b^{2}\right)^{2}=4\left(a^{2}y_{0}^{2}+b^{2}x_{0}^{2}-a^{2}b^{2}\right)}$

hyperbole

The solution for the hyperbolic case results from the ellipse case by replacing by (as with the orthoptic curves, see above ). ${\displaystyle b^{2}}$ ${\displaystyle -b^{2}}$

Comment: For the visualization of the curves see implicit curve .

Web links

• Special plane curves.
• Mathcurve: Orthoptic.
• Mathcurve: Isoptic.

literature

• Boris Odehnal: Equioptic Curves of Conic Sections. In: Journal for Geometry and Graphics. Volume 14, 2010, No. 1, pp. 29-43.
• Hermann Schaal: Linear Algebra and Analytical Geometry. Volume III, Vieweg, 1977, ISBN 3-528-03058-5 , p. 220.
• Jacob Steiner's lectures on synthetic geometry. B. G. Teubner, Leipzig 1867 ( Google Books ), Part 2, p. 186.
• Maurizio Ternullo: Two new sets of ellipse related concyclic points. In: Journal of Geometry. 2009, 94, pp. 159-173.
• Thierry Dana-Picard, Nurit Zehavi, Giora Mann: From conic intersections to toric intersections: The case of the isoptic curves of an ellipse. In: The Mathematics Enthusiast. Volume 9, Article 4 (PDF; 1.6 MB).

Individual evidence

1. ^ Quadrifolium in the English language Wikipedia.