Steiner's theorem (geometry)

Definition of the Steiner generation of a conic section

Perspective illustration between straight lines

The set of Steiner , also Steiner generation of a conic section , named after the mathematician Swiss Jakob Steiner , is an alternative way, a non-degenerate conic section in a projective plane over a body ( pappussche plane to be defined):

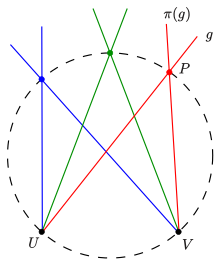
• If there is a projective but not perspective mapping of one tuft to the other for two straight tufts in two points (all straight lines through the point or ) , the intersection points of assigned straight lines form a non-degenerate conic section. (see 1st picture) ${\displaystyle U,V}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle \pi }$

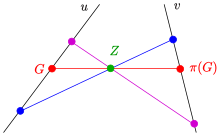
A perspective mapping of a straight line at a point onto the line at a point is understood to mean a bijection (one-to-one assignment) of the straight line in onto the straight line in such that assigned straight lines intersect on a fixed straight line . is called the axis of the perspective illustration (see 2nd picture). ${\displaystyle \pi }$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle \pi }$

A projective mapping is understood to be the execution of a finite number of perspective maps of a straight line in a row.

As a body you can z. For example , imagine the real numbers , the rational numbers or the complex numbers . But finite bodies are also allowed as coordinate areas. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {C} }$

Remark: The fundamental theorem for projective planes states that a projective mapping in a Pappus projective plane is already clearly determined by the specification of the images of 3 straight lines. This means that when Steiner creates a conic section, apart from the basic points, only the images of three straight lines have to be specified. The conic section is then clearly determined by these 5 determining pieces. ${\displaystyle U,V}$

Note: The term “perspective” comes from the dual statement: If the points of a straight line are projected from a point (center) onto a straight line , this mapping is called perspective (see dual case). ${\displaystyle u}$ ${\displaystyle Z}$ ${\displaystyle v}$

Simple example: If you move the point and its tuft of straight lines into the point in the first picture and then rotate the tuft in by a fixed angle , the displacement together with the rotation creates a projective mapping of the tuft of straight lines in onto the tuft of straight lines in . The resulting conic section is a circle because of the set of peripheral angles . ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle \varphi }$ ${\displaystyle U}$ ${\displaystyle V}$

example

Example of a Steiner generation of a conic section: construction of a point

In the following example, the images of the lines are given: . The projective image can be represented as a product (one behind the other) of the following perspective images : ${\displaystyle a,u,w}$ ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$ ${\displaystyle \pi }$ ${\displaystyle \pi _{b},\pi _{a}}$

1) is the perspective mapping of the tuft in on the tuft in with the axis . ${\displaystyle \pi _{b}}$ ${\displaystyle U}$ ${\displaystyle O}$ ${\displaystyle b}$

2) is the perspective mapping of the tuft in on the tuft in with the axis . ${\displaystyle \pi _{a}}$ ${\displaystyle O}$ ${\displaystyle V}$ ${\displaystyle a}$

One can convince oneself that the projective mapping actually has the claimed property . This means that the image and thus any number of points of the conic section can be constructed for any straight line . Since only the conic intersection point or lies on the straight line or , and are tangents of the conic section. ${\displaystyle \pi =\pi _{a}\pi _{b}}$ ${\displaystyle \pi (a)=b,\pi (u)=w,\pi (w)=v}$ ${\displaystyle g}$ ${\displaystyle \pi (g)=\pi _{a}\pi _{b}(g)}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u}$ ${\displaystyle v}$

The easiest way to prove that a conic section is created by this construction is to transition to an affine restriction with the straight line as the distance line, the point as the zero point of a coordinate system with the points as the distance points of the x or y axis and the point . The affine part of the conic section is then the hyperbola . ${\displaystyle w}$ ${\displaystyle O}$ ${\displaystyle U,V}$ ${\displaystyle E=(1,1)}$ ${\displaystyle y=1/x}$

Comment:

1. The Steiner generation of a conic section has concrete practical significance in the construction of ellipses , hyperbolas and parabolas .
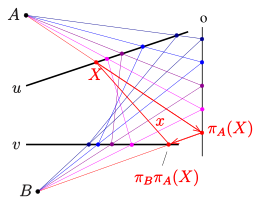
2. The figure for the construction of a point (3rd picture) is the 4-point expansion of Pascal's theorem .
3. The creation of the parabola can be found in projective conic section . ${\displaystyle y=x^{2}}$

Stone generation of a dual conic section

dual ellipse

Steiner generation of a dual conic section

Definition of a perspective map

Definitions and dual generation

If you dualize (see principle of duality ) a non-degenerate conic section of a projective plane, the tangents take on the role of the points:

A non-degenerate dual conic consists of the entirety of the tangents of a non-degenerate conic.

A dual conic section can also be generated using Steiner's method:

• If one has a projective , but not perspective, mapping of one row of points onto the other for two rows of points on two straight lines, the straight lines connecting the points assigned to them form a non-degenerate dual conic section. ${\displaystyle u,v}$ ${\displaystyle \pi }$

A perspective mapping of a row of points of a straight line on the row of points of a straight line is understood as a bijection (one-to-one assignment) of the points from to the points from in such a way that the connecting straight lines of assigned points intersect at a fixed point . is called the center of the perspective illustration (see picture). ${\displaystyle \pi }$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle \pi }$

A projective mapping is understood to be the execution of a finite number of perspective maps one after the other.

The validity of the generation of a dual conic section results from the duality principle for projective planes.

Examples

Dual conic section for two given perspective images ${\displaystyle \pi _{A},\pi _{B}}$

1: Two perspective images:
Given: (1) two straight lines , (2) a perspective image with a center that maps onto a third straight line , and (3) a perspective image with a center that maps onto . ${\displaystyle u,v}$
${\displaystyle \pi _{A}}$ ${\displaystyle A}$ ${\displaystyle u}$ ${\displaystyle o}$
${\displaystyle \pi _{B}}$ ${\displaystyle B}$ ${\displaystyle o}$ ${\displaystyle v}$

(4) The straight lines and must not go through the intersection of the straight lines ! ${\displaystyle AB}$ ${\displaystyle o}$ ${\displaystyle W}$ ${\displaystyle u,v}$

The projective mapping of the row of points from onto the row of points from is not in perspective. For each point, the straight line is therefore an element of a dual conic section that has not degenerated through the specifications. ${\displaystyle \pi =\pi _{B}\pi _{A}}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle X}$ ${\displaystyle x={\overline {X\pi (X)}}}$

(If (4) does not apply, a fixed point and the image is in perspective!) ${\displaystyle W}$ ${\displaystyle \pi }$

Steiner generation of a dual conic section: and its image points are given. The conic section, the tangents of which are generated here, goes through the points and has the tangents there . ${\displaystyle A,U,W}$ ${\displaystyle B,W,V}$ ${\displaystyle U,V}$ ${\displaystyle u,v}$

2: Three points and their images are given:
The following example is the dualization of the above example for the stone generation of a conic section.
The images of the points are given: . The projective image can be represented as a product (one behind the other) of the following perspective images : ${\displaystyle A,U,W}$ ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$ ${\displaystyle \pi }$ ${\displaystyle \pi _{B},\pi _{A}}$

1) is the perspective mapping of the row of points from to the row of points from with the center . ${\displaystyle \pi _{B}}$ ${\displaystyle u}$ ${\displaystyle o}$ ${\displaystyle B}$

2) is the perspective mapping of the row of points on to the row of points on with the center . ${\displaystyle \pi _{A}}$ ${\displaystyle o}$ ${\displaystyle v}$ ${\displaystyle A}$

One can convince oneself that the projective mapping actually has the claimed property . This means that the image and thus any number of tangents of the conic section can be constructed for any point . Since only the conic section line or passes through the point or , and points of the conic section and the straight lines are tangents in . ${\displaystyle \pi =\pi _{A}\pi _{B}}$ ${\displaystyle \pi (A)=B,\,\pi (U)=W,\,\pi (W)=V}$ ${\displaystyle G}$ ${\displaystyle \pi (G)=\pi _{A}\pi _{B}(G)}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle u,v}$ ${\displaystyle U,V}$

Individual evidence

1. ↑ Projective Geometry , short script, Uni Darmstadt (PDF; 180 kB), p. 16.
2. ^ Jacob Steiner's lectures on synthetic geometry , BG Teubner, Leipzig 1867 (at Google Books: [1] ), Part 2, p. 96 (in Google PDF version on p. 339).
3. ↑ Hanfried Lenz : Lectures on projective geometry , Akad. Verl. Leipzig, 1965, p. 56
4. ^ H. Lüneburg : The Euclidean plane and its relatives , p. 104.
5. ^ W. Blaschke : Projektive Geometrie , p. 56
6. ↑ Projective Geometry , short script, Uni Darmstadt (PDF; 180 kB), p. 10.
7. ^ Planar Circle Geometries, an Introduction to Moebius, Laguerre and Minkowski Planes. (PDF; 891 kB), p. 38.
8. ↑ H. Lenz: Lectures on projective geometry , BI, Mannheim, 1965, p. 49.