Perspective mapping

Perspective assignment is a term from projective geometry and describes in a projective plane a special relationship between one-dimensional basic structures , i.e. a row of points (all points of a straight line) or a straight line (all straight lines through a fixed point).

In the simplest case, the projection of one row of points onto another from one point represents a perspective assignment of two rows of points. However, a straight line can also be assigned to a row of points. Perspective assignments can be continued under sufficient conditions to perspectives (collineations) of the projective level.

A projective assignment between two basic structures is the execution of a finite number of perspective assignments one after the other. If two basic structures are assigned to one another through perspective or projective assignment, one also says that they are in a perspective or projective position .

The importance of perspective or projective assignments can be seen in the main theorem of projective geometry and Steiner's theorem on the creation of a conic section.

Row of dots and straight lines in perspective position

The points on and the straight lines through are assigned to each other in perspective ${\displaystyle P}$ ${\displaystyle a}$ ${\displaystyle g}$ ${\displaystyle Z}$

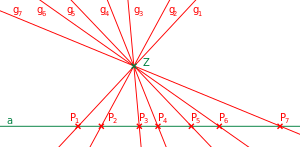
The geometrically simplest perspective assignment of one-dimensional structures in a projective plane is the assignment between a row of points , i.e. the set of points of a straight line in the plane and a line bundle of the same plane, i.e. the set of straight lines through a fixed point on the plane that is not with incised. The assignment can be formally defined as follows: ${\displaystyle a}$ ${\displaystyle Z}$ ${\displaystyle a}$

${\displaystyle \Delta (a,Z):a\ni P\mapsto (P+Z)\ni Z.}$

This means that each point on the connecting line is assigned to the picture see the upper right. The assignment is well-defined and bijective based on the incidence axioms for projective levels alone. This shows: ${\displaystyle P}$ ${\displaystyle a}$ ${\displaystyle P+Z}$ ${\displaystyle \Delta (a,Z)}$

1. In a projective plane, each projective row of points is, as an incidence structure, isomorphic to the incidence structure given by the tuft structure, provided it is not located on. You can see that this last condition can be omitted by repeated perspective assignment. ${\displaystyle (a,\{a\},I_{a})}$ ${\displaystyle (\{g|g\mathop {I^{-1}} Z\},\{Z\},(I^{-1})_{Z})}$ ${\displaystyle Z}$ ${\displaystyle a}$
2. This results in: In every projective plane all rows of points are incidence isomorphic to one another and to all straight line tufts. In particular, the “point sets” of these structures are equally powerful .
3. In concrete terms, this means for finite levels: every straight line contains the same number of points , every tuft contains the same number of straight lines and it is . That means: every finite level is a symmetrical - block diagram . The number here is the order of the finite plane. ${\displaystyle v_{1}=q+1}$ ${\displaystyle b_{1}=q+1}$ ${\displaystyle v_{1}=b_{1}}$ ${\displaystyle 2-(q^{2}+q+1,q+1,1)}$ ${\displaystyle q}$
4. In every Papposian level there is a correlation of the level into its (in the sense of the incidence structure) dual level , which continues the assignment . ${\displaystyle ({\mathcal {P}},{\mathcal {G}},I)}$ ${\displaystyle ({\mathcal {G}},{\mathcal {P}},I^{-1})}$ ${\displaystyle \Delta (a,Z)}$
5. In each Desargue's projective level, a double ratio defined on a row of points can be transferred to point clusters and vice versa through the assignment.
6. In every arranged level , the arrangement of a row of points can be transferred to a cluster of points and vice versa through the assignment.
7. In every topological projective plane , point clusters and point rows are homeomorphic .

Two rows of points in perspective

The point triple of the row of points lies on from the center in perspective to the point triple of the row of points ${\displaystyle (A_{1},A_{2},A_{3})}$ ${\displaystyle a}$ ${\displaystyle Z}$ ${\displaystyle (B_{1},B_{2},B_{3})}$ ${\displaystyle b}$

If one a perspective assignment of the row of points on a straight line on the dot clusters of the straight line passing through a point having such a tuft from the same point on the dot row another line composed , then one obtains a perspective mapping between the rows of and . The prerequisite is that the common center does not lie on either of the two straight lines : ${\displaystyle a}$ ${\displaystyle Z}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a,b}$

${\displaystyle \pi =\pi (a,Z,b):=\left(\Delta (b,Z)\right)^{-1}\circ \Delta (a,Z)}$

You can also define this assignment yourself:

${\displaystyle \pi (a,Z,b)(A)=B:\Leftrightarrow \left(A\in a\land B=(A+Z)\cap b\right)}$

The intersection of the connecting straight line with the straight line is assigned to a point. The second definition is preferable because the central perspective mapping from the point of the picture may theoretically easier (no duality!) And goes on under weaker conditions: ${\displaystyle A\in a}$ ${\displaystyle A+Z}$ ${\displaystyle b}$ ${\displaystyle Z}$

Cross line construction in a Desargue plane

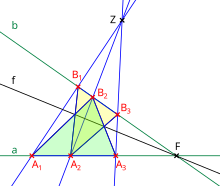
• In a Desarguese level there is at least one projectivity that continues. It can be chosen as a perspective with the center and its axis, if the plane also satisfies the Fano axiom , can be constructed from two different point-image point pairs, if there is not the intersection point below that, which is assigned by itself , see also The figure on the right: The (only possible) center for perspectivity is the intersection of the two tracks . A fixed point , ie a point on the axis is determined as the intersection of prototype line with its image straight so . ${\displaystyle \pi =\pi (a,Z,b)}$ ${\displaystyle Z}$ ${\displaystyle (A_{1},\pi (A_{1})),(A_{2},\pi (A_{2}))}$ ${\displaystyle F=a\cap b}$ ${\displaystyle \pi }$ ${\displaystyle \left(\pi (F)=F\right)}$ ${\displaystyle Z=(A_{1}+B_{1})\cap (A_{2}+B_{2})}$ ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle a=A_{1}+A_{2}}$ ${\displaystyle b=B_{1}+B_{2}}$ ${\displaystyle F=a\cap b}$

A second point of the axis results from two point-image point pairs by connecting them “crosswise” as shown in the figure (the lines etc. in the figure). Please note that the triangles highlighted in color are from central perspective and that the axis for this configuration according to Desargue's theorem is: The intersection points of assigned triangle sides are the two "cross intersection points" shown in the picture and the fixed point described above . ${\displaystyle A_{1}B_{2}}$ ${\displaystyle Z}$ ${\displaystyle f}$ ${\displaystyle F}$

• In any projective plane is the general plane in a resumable collineation when in the bilge Barlotti figure the plane to a pair with belongs. The collineation does not need to be clearly defined, but then, if the plane fulfills the Fano axiom, there is also a projectivity that continues the assignment, a perspectivity with a center . ${\displaystyle \mathbb {P} }$ ${\displaystyle \pi (a,Z,b)}$ ${\displaystyle Z}$ ${\displaystyle {\mathcal {B}}(\mathbb {P} )}$ ${\displaystyle (c,Z)\in {\mathcal {B}}(\mathbb {P} )}$ ${\displaystyle c\not \in \{a,b\}}$ ${\displaystyle Z}$

The (central) perspective assignment between two projective straight lines can also be specialized in an affine manner: If a far point, then induces a bijective parallel projection on the affine subsets of the point rows . These parallel projections play a similar central role in synthetic affine geometry as do the perspectives in projective geometry. ${\displaystyle Z}$ ${\displaystyle \pi }$ ${\displaystyle a,b}$

notation

The fact that an ordered set of collinear points lies in perspective of an ordered set of the same kind can be used to define a relation on the set of all - tuples of collinear points . This relation is (in the example in the figure above right) as ${\displaystyle (A_{1},A_{2},\ldots )}$ ${\displaystyle T}$ ${\displaystyle n}$ ${\displaystyle \left(n\in \mathbb {N} ,\,n\geq 2\right)}$ ${\displaystyle T:=\bigcup _{n=2}^{\infty }T_{n};T_{n}:=\{(A_{1},A_{2},\ldots A_{n})|\exists g\in {\mathcal {G}}:A_{1},A_{2},\ldots A_{n}\in g\}}$

${\displaystyle (A_{1},A_{2},A_{3})\doublebarwedge (B_{1},B_{2},B_{3});\quad (A_{1},A_{2},A_{3},F)\doublebarwedge (B_{1},B_{2},B_{3},F)}$ etc. noted

or more precisely, with the mediating center above the relation symbol as

${\displaystyle (A_{1},A_{2},A_{3}){\stackrel {Z}{\doublebarwedge }}(B_{1},B_{2},B_{3});\quad (A_{1},A_{2},A_{3},F){\stackrel {Z}{\doublebarwedge }}(B_{1},B_{2},B_{3},F)}$

written down. If this applies to (not necessarily different) centers , then you write . If one continues this relation transitively (over a finite number instead of just two mediating centers) then the relation in and in each subset is an equivalence relation . One then says of the points that they are projectively related to one another or they are also projective to one another . Note: ${\displaystyle Y,Z:\,\left[(A_{1},A_{2},A_{3}){\stackrel {Y}{\doublebarwedge }}(B_{1},B_{2},B_{3})\right]\land \left[(B_{1},B_{2},B_{3}){\stackrel {Z}{\doublebarwedge }}(C_{1},C_{2},C_{3})\right]}$ ${\displaystyle (A_{1},A_{2},A_{3})\barwedge (C_{1},C_{2},C_{3})}$ ${\displaystyle \barwedge }$ ${\displaystyle T}$ ${\displaystyle T_{n}\subset T}$ ${\displaystyle (A_{1},A_{2},A_{3});(C_{1},C_{2},C_{3})}$

1. For the perspective position to one another (relation ) and the projective position (relation ) to one another of points, the sequence of both point sets is important! The tuple notation used here, which formally ensures this, is usually not (consistently) used in the literature . ${\displaystyle \doublebarwedge }$ ${\displaystyle \barwedge }$
2. In general, there must be no collineation for two tuples that are perspective or projectively related to one another, which maps one tuple to the other! If such a collineation exists, then there is also a projectivity with this property. This is always the case for projectively related tuples over a Desarguean plane, and over every plane trivially if the two tuples are identical. Each tuple from is apparently projective to itself, usually it is agreed that such a tuple should even be in perspective to itself, the mediating center outside the carrier line is then arbitrary. Since identity is a projectivity, there is also a continuing collineation with it, but this can at most be the only continuation for one level of Lenz-Barlotti class I.1 . ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle T}$
3. The modern notation explained here for ways of speaking of the 19th century is basically a superfluous formalism due to the language of modern set theory : The bijective mapping given by is itself a relation; the point series can be used as a counting set by itself, using it if necessary , equips it with a well-order , and thus any arbitrary, even infinite, subset of the series of points from correctly "numbering". The same applies to the rows of points that are projectively assigned to one another, that is to say are in the relation to one another. ${\displaystyle \pi =\pi (a,Z,b)}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \barwedge }$

Two straight lines in a perspective position

The straight lines through are in perspective to the straight lines through in relation to the axis . For the red lines drawn in the picture this is noted as. ${\displaystyle Y}$ ${\displaystyle Z}$ ${\displaystyle a}$ ${\displaystyle (g_{1},g_{2},g_{3}){\stackrel {a}{\doublebarwedge }}(h_{1},h_{2},h_{3})}$

Dual perspectives for assignment of two dot rows of a center of the position of two perspective pencil of lines (with the points is as carriers) from an axis of defined. The axis must not lie in any of the assigned clusters, i.e. it must not contain any of the points . ${\displaystyle Y,Z}$ ${\displaystyle a}$ ${\displaystyle Y,Z}$

${\displaystyle \Pi (Y,a,Z):=\Delta (a,Z)\circ \left(\Delta (a,Y)\right)^{-1}}$

Independent definition:

${\displaystyle \Pi (Y,a,Z)(g)=(g\cap a)+Z;\;\left(Y\in g\right)}$

For this perspective mapping (axial-) of straight tuft through to the pencil of lines through the axis of apply the dual to the statements of the previous paragraph statements. ${\displaystyle \Pi (Y,a,Z)}$ ${\displaystyle Y}$ ${\displaystyle Z}$ ${\displaystyle a}$

The relation notation (relation ) and a transitive continuation (relation ) between tuples of straight lines from each point cluster is agreed analogously to the one described above for point tuples, the ways of speaking are also analogous: triples with lying (from the axis ) perspective to each other , are therefore also projectively related to one another , etc. ${\displaystyle {\stackrel {a}{\doublebarwedge }}}$ ${\displaystyle \barwedge }$ ${\displaystyle n}$ ${\displaystyle (g_{1},g_{2},g_{3}){\stackrel {a}{\doublebarwedge }}(h_{1},h_{2},h_{3})}$ ${\displaystyle a}$ ${\displaystyle \left((g_{1},g_{2},g_{3})\barwedge (h_{1},h_{2},h_{3})\right)}$

Row of dots and conic section or oval in perspective position

In a Papposian projective plane, which satisfies the Fano axiom, every non-degenerate conic section, in the figure a circle, can be related in perspective and bijective to a row of points of a straight line that does not incise with the center . The tangent “opposite” the center was chosen as the straight line for this illustration. This is not an essential prerequisite: If you choose any other straight line that does not contain the center, then you can also map to an actual point , with the tangent at in . ${\displaystyle a}$ ${\displaystyle Z}$ ${\displaystyle a}$ ${\displaystyle a'}$ ${\displaystyle Z}$ ${\displaystyle a'\cap t}$ ${\displaystyle t}$ ${\displaystyle k}$ ${\displaystyle Z}$

The figure on the right shows a circle and a straight line , the point sets of which are in perspective to one another from the center on the circular line. The assignment assigns the intersection point (in the projectively closed plane) to each point of the row of points , which is different from , unless this intersection only contains this center . The connecting lines that convey the assignment are shown in the figure by blue half-lines. The "connecting straight line " is the tangent to at the point , because this tangent has a "double-counting" intersection with . With this choice, this straight line meets this straight line at its far point, indicated in the picture by two arrows. ${\displaystyle k}$ ${\displaystyle a}$ ${\displaystyle Z}$ ${\displaystyle \pi =\pi (a,Z,k)}$ ${\displaystyle P}$ ${\displaystyle (P+Z)\cap k}$ ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle t:=Z+Z}$ ${\displaystyle k}$ ${\displaystyle Z}$ ${\displaystyle k}$ ${\displaystyle a}$

It was already explained above that the mapping bijectively assigns the row of points to the set of straight lines. The answers to the following three questions about the relationship between points on a circular line (more generally: points on a non-degenerate conic section ) say that it is a bijective function (the injectivity is then trivially given): ${\displaystyle \Delta (a,Z)}$ ${\displaystyle {\mathcal {Q}}}$

1. Does every straight line through except the tangent in the conic section intersect the conic section again, so is it definable for every point? ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle \pi }$
2. Can the mapping be clearly defined or can there be straight lines that meet more than twice? ${\displaystyle P+Z}$ ${\displaystyle k}$
3. Is the mapping surjective, so is every point on the circular line hit by a straight line?

Justifications

1. If a straight line did not intersect the conic section at any other point except in , then this straight line would also be a tangent at the point . However, for purely computational reasons (non-degenerate conic section!), This only occurs once when inserting the linear equations into the quadratic equation. In the picture when the far point is from . ${\displaystyle P_{0}+Z}$ ${\displaystyle Z}$ ${\displaystyle Z}$ ${\displaystyle P_{0}}$ ${\displaystyle a}$
2. Straight lines that meet the conic section more than twice cannot exist, otherwise the conic section would have degenerated. ${\displaystyle P+Z}$
3. A point not hit has a straight line connecting it with the center, but this intersects , so it is hit. ${\displaystyle Q\neq Z}$ ${\displaystyle a}$ ${\displaystyle Q}$

Inferences

For an oval in a Papposian plane, which satisfies the Fano axiom, the perspective assignment from a center to a straight line is also a bijective, perspective assignment; this is exactly how the ovals are defined. Therefore the following statements apply to every quadric as well as to every oval in such a plane: ${\displaystyle {\mathcal {Q}}}$ ${\displaystyle Z\in {\mathcal {Q}}}$ ${\displaystyle a\not \ni Z}$ ${\displaystyle {\mathcal {Q}}}$ ${\displaystyle {\mathcal {Q}}}$

• The question of continuability does not arise for the assignment , since collinear points are related to non-collinear points. ${\displaystyle \pi =\pi (a,Z,{\mathcal {Q}})}$
• If the plane is finite, then contains exactly elements, where is the order of the plane. ${\displaystyle {\mathcal {Q}}}$ ${\displaystyle q+1}$ ${\displaystyle q}$
• To be (in various ways, depending on the choice of ) one-dimensional coordinate introduce, thus this curve to a one-dimensional projective space above the body of the coordinate plane. ${\displaystyle {\mathcal {Q}}}$ ${\displaystyle Z,a}$
• An arrangement of the projective plane induces a unique arrangement on each circle and vice versa.
• In a topological projective plane is homeomorphic to every projective line. Special: A straight line in a topological projective plane is a topological circle. ${\displaystyle {\mathcal {Q}}}$

Projective mappings and the law of projective geometry

A perspective assignment between two different straight lines of a projective plane. If several such assignments are linked , one speaks of a projective assignment between the definition area of ​​the first assignment , the row of points of a straight line and the image area of ​​the last assignment , which is a row of points on a straight line . Then it can be. Every perspective assignment is also a projective assignment, but generally not the other way around. In the picture, the perspective relation and therefore also the generalized projective relation apply . ${\displaystyle \pi :a\rightarrow b}$ ${\displaystyle \pi _{n}\circ \cdots \circ \pi _{1}}$ ${\displaystyle \pi _{1}}$ ${\displaystyle a_{1}}$ ${\displaystyle \pi _{n}}$ ${\displaystyle a_{n}}$ ${\displaystyle a_{1}=a_{n}}$ ${\displaystyle (A_{1},A_{2},A_{3}){\stackrel {Z}{\doublebarwedge }}(B_{1},B_{2},B_{3})}$ ${\displaystyle (A_{1},A_{2},A_{3})\barwedge (B_{1},B_{2},B_{3})}$

• A projective assignment is a concatenation of perspective assignments (see above) between the rows of points of two different projective straight lines.

The following statement was in the geometry of the location of the 19th century as a law of projective geometry refers to:

A projectivity is determined when three points of a straight line and the corresponding three of the other straight lines are given.

With this formulation of the sentence should be noted:

1. “Projectivity” here denotes a projective assignment , and not a projective collineation of the entire plane or even of space! Nothing is said here about the existence or uniqueness of such a continuation .
2. In this context, it is assumed that both projective straight lines lie in a common plane, i.e. that they intersect each other equally. The linked perspective assignments can then also be made entirely on this level.
3. The correspondence of the sentence ("corresponding points") is in the more modern formulation a relation between point triples , that is, between ordered sets of three points ( different for this sentence ). In other words: It is important for the sentence which of the three points on the first straight line “corresponds” to which on the second.

A modern formulation that takes these three conditions into account is:

Axiom P7 ′: Let there be different straight lines in a projective plane. Let there be triples of different points. Then there is exactly one projective assignment , so that applies to this projective assignment, see also the first figure on the right. ${\displaystyle a,b}$ ${\displaystyle A_{1},A_{2},A_{3}\in a;B_{1},B_{2},B_{3}\in b}$ ${\displaystyle \pi :a\rightarrow b}$ ${\displaystyle (A_{1},A_{2},A_{3})\barwedge (B_{1},B_{2},B_{3})}$

Dual to the perspective or  projective assignment between two rows of points, the corresponding assignments for the straight line are defined by two points , in the picture the assignment is axial-perspective from the axis . One writes for the reproduced concurrent lines: . ${\displaystyle Y,Z}$ ${\displaystyle a}$ ${\displaystyle (g_{1},g_{2},g_{3}){\stackrel {a}{\doublebarwedge }}(h_{1},h_{2},h_{3})}$

The following variants of the main clause are equivalent statements about a projective level and equivalent to Pappos's theorem (PA):

• Axiom P7 ′
• Axiom P7: Let it be a straight line in a projective plane. Let there be two triples from three different points . Then there is at most one projective assignment with respect to which applies. ${\displaystyle a}$ ${\displaystyle (A_{1},A_{2},A_{3}),(B_{1},B_{2},B_{3})}$ ${\displaystyle a}$ ${\displaystyle \pi :a\rightarrow a}$ ${\displaystyle (A_{1},A_{2},A_{3})\barwedge (B_{1},B_{2},B_{3})}$
• Axiom P7 ″: Let there be different straight lines in a projective plane, their point of intersection. Then every projective assignment that fixes (that is, with ) a perspective assignment. ${\displaystyle a,b}$ ${\displaystyle F=a\cap b}$ ${\displaystyle \pi :a\rightarrow b}$ ${\displaystyle F}$ ${\displaystyle \pi (F)=F}$

For each projective level, the three named P7 statements are equivalent to the dualized statements. As an example, the dual form of P7 :

D7: Let it be a point in a projective plane. Let two triples from three different straight lines go through . Then there is at most one projective assignment with respect to which applies. ${\displaystyle Z}$ ${\displaystyle (g_{1},g_{2},g_{3}),(h_{1},h_{2},h_{3})}$ ${\displaystyle Z}$ ${\displaystyle \Pi :\{g|g\ni Z\}\rightarrow \{g|g\ni Z\}}$ ${\displaystyle (g_{1},g_{2},g_{3})\barwedge (h_{1},h_{2},h_{3})}$

literature

• Albrecht Beutelspacher , Ute Rosenbaum: Projective geometry . From the basics to the applications (=  Vieweg Studium: advanced course in mathematics ). 2nd, revised and expanded edition. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X .
• Arrigo Bonisoli: On collineation groups of finite planes . Socrates Intensive Program, Dipartimento di Matematic a Università della Basilicata, Potenza, Italy ( ugent.be [PDF; accessed on January 8, 2012] As the title suggests: group structure of the collineation group).
• Harold Scott MacDonald Coxeter : Real Projective Geometry of the Plane . After the 2nd engl. Edition translated by W. Burau. Ed .: Wilhelm Blaschke (=  Mathematical Individual Writings . Volume 3 ). 1st German edition. R. Oldenbourg, Munich 1955 (The textbook brings the classic, real "geometry of the situation" of the 19th century in a relatively modern formulation. Above all, the author or translator explains in detail who certain ideas and ways of speaking are based on and the translator explains differences between German and American usage).
• Erich Hartmann: Projective Geometry . Technical University, Darmstadt 2006 ( mathematik.tu-darmstadt.de [PDF; accessed on January 8, 2012] short script).
• Lars Kadison, Matthias T. Kromann: Projective Geometry and Modern Algebra . Birkhäuser, Boston / Basel / Berlin 1996, ISBN 3-7643-3900-4 (Consequences of the Fano axiom and the theorems of Desargues and Pappos for the transitivity properties of projective groups).
• Günter Pickert : Projective levels . 2nd Edition. Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-07280-2 (application of perspectives especially in non-Desarguese levels).
• Hans Walser: Projective images, graphic approach . Eidgenössische Technische Hochschule, Zurich ( ethz.ch [PDF; accessed on January 8, 2012] lecture notes; numerous illustrations, most of which, however, belong to exercises and must therefore be completed (following instructions in the text)).

Law of Projective Geometry

• Harold Scott MacDonald Coxeter : Real Projective Geometry of the Plane . After the 2nd engl. Edition translated by W. Burau. Ed .: Wilhelm Blaschke (=  Mathematical Individual Writings . Volume 3 ). 1st German edition. R. Oldenbourg, Munich 1955 (The textbook brings the classic, real "geometry of the situation" of the 19th century in a relatively modern formulation. Above all, the author or translator explains in detail who certain ideas and ways of speaking are based on and the translator explains differences between German and American usage).
• Karl Georg Christian von Staudt : Geometry of the situation . 1857, § 110, p. 52 (formulation and proof of the main theorem of projective geometry for the real case).

References and comments

1. ↑ ^{a b c} The plus sign between points is understood here according to Pickert (1975) in such a way that the sum of the points represents the straight line connecting them. In Desargue's case, the standard model is actually the sum of two subspaces of a (left) vector space.
2. ↑ denotes the incidence relation restricted to the row of points . ${\displaystyle I_{a}}$ ${\displaystyle a}$
3. ↑ For the parameters in the designation one applies the incidence axiom: Two straight lines intersect at exactly one point. For the total number of points, all points on all straight lines are counted from one point . This number is . In doing so, you initially counted several times, namely times, and therefore deducted from the product. Beutelspacher and Rosenbaum (2004) ${\displaystyle t=2,v_{0}=q^{2}+q+1}$ ${\displaystyle t-(v_{0},v_{1},b_{2})}$ ${\displaystyle t=2,b_{2}=1}$ ${\displaystyle v_{0}}$ ${\displaystyle P_{0}}$ ${\displaystyle P_{0}}$ ${\displaystyle b_{1}\cdot v_{1}-q=(q+1)^{2}-q}$ ${\displaystyle P_{0}}$ ${\displaystyle (q+1)}$ ${\displaystyle q}$
4. ↑ ^{a b c} For this it is not necessary that the perspective assignment to a correlation of the entire level can be continued on its dual level.
5. ↑ If one looks at two cross- sectional configurations and the triangles in isolation, then one also has a pappus configuration, but because the triples are in perspective to each other, Desargue's sentence applies. Kadison and Kromann (1996), chapter 6: The Fundamental theorem for perspectivities on a line
6. ↑ After Coxeter (1955) p. 27. According to Coxeter, the notation goes to Veblen and Young: Projective Geometry . tape I . Boston 1910. back.
7. ↑ In any planes, if it is possible over a finite number of centers, a maximum of 4 mediating centers is sufficient, in Desargue’s planes three if the point tuples are on the same straight line, otherwise two. Pickert (1975)
8. ↑ For example also in Coxeter (1955)!
9. ↑ Coxeter (1955), p. 28.
10. ↑ ^{a b c} Beutelsbacher, Rosenbaum (2004), Chapter 4: Quadratic sets .
11. ↑ The choice of the center on the circular line is essential for this argument: The quadratic equation to be solved has a solution in the coordinate field (Pappos plane) and thus (assuming the Fano axiom, which applies) also a second solution, which is either double -counting is the same or different from the first. ${\displaystyle K}$ ${\displaystyle \operatorname {char} (K)\neq 2}$
12. ↑ by Staudt (1857)
13. ↑ Name and formulation of the sentence from Coxeter (1955), 4: Theorem of Pappos , 4.2: The main law of projective geometry .
14. ↑ ^{a b} Translated from Kadison and Kromann (1996): 6.1: The Fundamental theorem: Axiom P7.
15. ↑ The intersection point may also appear in one or both triples! Kadison and Kromann (1996): 6.1: The Fundamental theorem: Axiom P7 ${\displaystyle S=a\cap b}$
16. ↑ Translated from Kadison and Kromann (1996): 6.1: The Fundamental theorem: Axiom P7.