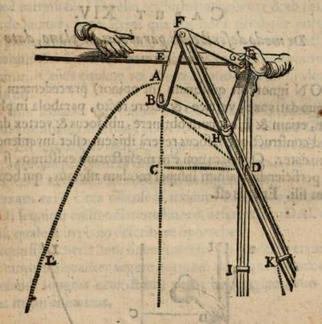
Parabolic circle by Frans van Schooten

Parabolic circle by Frans van Schooten

The parabolic circle by Frans van Schooten is a mechanism that creates the shape of a parabola . In 1657, Frans van Schooten published a parabolic circle in LIBER IV in his work EXERCITATIONUM MATHEMATICARUM LIBRI QUINQUE.

The parabolic circle essentially consists of four parts:

1. a fixed main runner, the front edge of which runs through the point , ${\displaystyle E}$
2. a diamond with the points of articulation with the circular needle in the first fixed point of the diamond, ${\displaystyle BHGF,}$ ${\displaystyle B,}$
3. a split diagonal stick with the pen in ${\displaystyle |FK|,}$ ${\displaystyle D,}$
4. a movable guide rail arranged orthogonally to the main rail, with the point as the second fixed point of the diamond. ${\displaystyle |GI|}$ ${\displaystyle G,}$

The guide rail is slidably mounted on the main rail. Together they form a right angle . A so-called sliding block at the point of the guide rail enables a movable connection between the split diagonal bar and the guide rail ${\displaystyle |GI|}$ ${\displaystyle D}$ ${\displaystyle |GI|,}$ ${\displaystyle |FK|}$ ${\displaystyle |GI|.}$

The two hands drawn should clarify the handling of the parabolic circle. After inserting the compass into the focal point, hold the main rail with one hand. With the other hand, using a handle at the point, a turning and sliding movement is performed. As a result, the guide rail together with the diagonal rod forces the pen into a parabolic path. ${\displaystyle B,}$ ${\displaystyle G}$ ${\displaystyle B}$ ${\displaystyle |GI|,}$ ${\displaystyle |FK|,}$ ${\displaystyle D}$

A possible reason why the curves drawn with Frans van Schooten's parabolic circle are exact parabolas is described in the following section, Geometric Consideration .

Geometric view

To clarify why the curves generated with the parabolic circle are exact parabolas, in the following first a parabolic point is determined in a basic construction according to the definition with a guideline and then the parabolic circle is basically incorporated. The sequence of movements is explained in Draw a parabola . The names of the points are taken from the above original illustration of parabolic circles by Frans van Schooten . ${\displaystyle D}$

Parabolic point as defined with guideline

Figure 1: Parabolic point as defined with guideline ${\displaystyle l}$

With the names of the points used in Figure 1, a decisive statement of the definition with guideline reads :

"A parabola is the geometric location of all points whose distance from a special fixed point - the focal point  - is the same as the distance from a special straight line - the guideline  ." ${\displaystyle D}$ ${\displaystyle d(D,B)}$ ${\displaystyle B}$ ${\displaystyle d(D,l)}$ ${\displaystyle l}$

After drawing in the guideline , the parabolic axis is drawn; it gives the intersection . Now you set the focal point at a freely selectable distance from the guideline (the greater this distance, the flatter the curvature of the parabola becomes), e.g. B. below the point for a downwardly open parabola. With the drawn guideline and the selected focal point , the parabola is already determined mathematically. The parabola (green) can e.g. B. can be entered using a dynamic geometry software (DGS) . ${\displaystyle l}$ ${\displaystyle E}$ ${\displaystyle B}$ ${\displaystyle l}$ ${\displaystyle E}$ ${\displaystyle l}$ ${\displaystyle B}$

If one draws a circle estimated opening each have a circular arc at and around the just on the guideline resulting intersection ; the points of intersection are and A subsequent line through and is also the perpendicular bisector of the distance The ensuing vertical to guidance from the point intersecting the perpendicular bisector in the searched point and brings the isosceles triangle ${\displaystyle B}$ ${\displaystyle l}$ ${\displaystyle G}$ ${\displaystyle R}$ ${\displaystyle S.}$ ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle M_{S}}$ ${\displaystyle |BG|.}$ ${\displaystyle l}$ ${\displaystyle G}$ ${\displaystyle M_{S}}$ ${\displaystyle D}$ ${\displaystyle GBD.}$

The isosceles triangle with ${\displaystyle GBD}$

${\displaystyle |DB|=|DG|,}$

is a half diamond in which the perpendicular to the center is a tangent to the parabola . The tangent touches the parabola at the point. Thus the constructed point is a parabola point. ${\displaystyle M_{S}}$ ${\displaystyle D.}$ ${\displaystyle D}$

Construction of the parabolic circle

Fig. 2: Outline sketch

• So that the parabolic circle can draw a complete parabolic line, it is necessary to place the parabolic point (drawing pen ) within the diamond. It should be noted that in the original illustration above, Frans van Schooten's parabolic circle lies outside the diamond. With this position of only a shortened parabolic line can be drawn; z. B. counterclockwise until the pen is at the hinge point of the diamond. ${\displaystyle D}$ ${\displaystyle D}$ ${\displaystyle D}$ ${\displaystyle D}$ ${\displaystyle H}$

The schematic diagram opposite (Fig. 2) is a continuation of the basic construction of the parabolic point as defined with a guideline ${\displaystyle l}$ (Fig. 1). The parabola (green) has been hidden for a better overview. The necessary points and as well as the guideline and the perpendicular bisector are determined, so it only needs a simple incorporation of the essential parts of the parabolic circle above-described. ${\displaystyle B,G}$ ${\displaystyle D}$ ${\displaystyle l}$ ${\displaystyle M_{S}}$

First, the two side lengths and the rhombus, with an estimated compass opening, larger than the distance , are determined on the vertical line . The connection of the points of articulation with and with follows and completes the diamond with the isosceles triangle (light blue). This is followed by drawing in the diagonal bar from the pivot point beyond . Finally, the guide rail is drawn as a vertical (orthogonal) on the guideline at the point . It cuts the diagonal bar , as indicated, also in the parabolic point of the isosceles triangle (pink). ${\displaystyle {\overline {FG}}}$ ${\displaystyle {\overline {GH}}}$ ${\displaystyle |GD|}$ ${\displaystyle M_{S}}$ ${\displaystyle B}$ ${\displaystyle F}$ ${\displaystyle B}$ ${\displaystyle H}$ ${\displaystyle BHGF}$ ${\displaystyle BGF}$ ${\displaystyle |FK|}$ ${\displaystyle F}$ ${\displaystyle H}$ ${\displaystyle |GI|,}$ ${\displaystyle l}$ ${\displaystyle G}$ ${\displaystyle |FK|}$ ${\displaystyle D}$ ${\displaystyle GBD}$

Draw a parabola

Fig. 3: Animated principle sketch

If the parabolic compass is moved by hand as described above (Figure 3), the hinge point runs along the guideline and the pen ( ) runs in the gap of the diagonal rod The guide rail forces the diagonal rod to act as a constant vertical line of the continuously changing isosceles triangles and ,. From this it follows: In every rotated position of the parabolic circle applies ${\displaystyle G}$ ${\displaystyle l}$ ${\displaystyle D}$ ${\displaystyle |FK|.}$ ${\displaystyle |GI|}$ ${\displaystyle |FK|}$ ${\displaystyle M_{S},}$ ${\displaystyle GBF}$ ${\displaystyle GBD}$

${\displaystyle |DB|=|DG|.}$

This shows: The curves drawn with the parabola are exact parabolas.

Applications

Image 4: Parabolic circle, animated concept drawing, reproduction of the replica from the mathematics laboratory of the University of Münster

• In the station of the project mathematics laboratory of the WWU Münster , a stable and practicable replica of the parabolic circle by Frans van Schooten with small changes is shown. With the help of this real model, students can, among other things, experimentally explore the components, functionality and the mathematical background of the parabolic circle.

The adjacent concept drawing (Fig. 4) is a reproduction of this replica. The designations of the relevant points correspond to those in Figure 1.

Structure of the replica, basic principle by Frans van Schooten:

1. Base plate (light gray)
2. Cross slide (green)
3. Slide guide (light blue) with attachment (anthracite) and stops (black)
4. Guide rail (acid green) with sliding block (black)
5. Diamond (anthracite)
6. Diagonal bar (honey colored)
7. Stop rail (ocher) with guideline (blue) for the drawing sheet (white) ${\displaystyle l}$
8. Guide of the focus rail (light blue)
9. Focus rail (gray), adjustable rail for adjusting the focus ${\displaystyle B.}$

• In 2015, Christian van Randenborgh published a wooden replica from 2010 in his work Tools for imparting knowledge in mathematics lessons. In it, he explains the circle of parables using, among other things, the following six, as he says, “ideas”:

“The idea behind the parabolic compass is to draw parabolas (point P = pen).

The wooden replica shows that the essential mechanical idea of the parabolic circle is the joint diamond (FRLQ).

With the parabolic circle, the mathematical idea can be found in the construction and in the functionality.

The didactic idea will be discussed in more detail later. ³³

In a corresponding use in the classroom with the students one arises Terms idea how to draw with the parabolic compass and what you can use it.

All of this indicates that the parabolic circle also embodies a certain interest in mathematics and a certain view of geometry, in short: it carries a cultural-historical idea . "

See also

Thread construction of a parabola

literature

• C. Edward Sandifer: Van Schooten's Ruler Constructions . In: Convergence . August 2010, doi : 10.4169 / convergence20141101 (English).

Individual evidence

1. ↑ Frans van Schooten: EXERCITATIONUM mathematicarum LIBRI QUINQUE. Lugdunum Batavorum [= Leiden ]: Johannes Elsevirius, 1656–1657, table of contents, p. 7 online copy (Google) , accessed on February 6, 2019.
2. ↑ Frans van Schooten: EXERCITATIONUM MATHEMATICARUM, LIBER IV. SIVE DE ORGANICA CONICARUM SECTIONUM IN PLANO DESCRIPTIONE, ... title page, p. 293 online copy (Google) , accessed on February 6, 2019.
3. ↑ Frans van Schooten: EXERCITATIONUM MATHEMATICARUM LIBER IV… Parabolic Circle, pp. 356–359 Online copy (Google) , accessed on February 6, 2019.
4. ↑ Sabine Baum: Digital tools. Simulations and mathematical modeling . In: Gilbert Greefrath, Hans-Stefan Siller (Hrsg.): Reality references in mathematics lessons . Springer Spectrum, Wiesbaden 2018, ISBN 978-3-658-21939-0 , 5.5 Mathematical Instruments - The Parabolic Circle, p. 104–105 , Fig. 5.12 a ( limited preview in Google Book Search [accessed on February 6, 2019]).
5. ↑ MATHEMATICS laboratory, describing the project. Retrieved February 6, 2019 . 
6. ↑ Sabine Baum: Digital tools. Simulations and mathematical modeling . In: Gilbert Greefrath, Hans-Stefan Siller (Hrsg.): Reality references in mathematics lessons . Springer Spectrum, Wiesbaden 2018, ISBN 978-3-658-21939-0 , 5.5 Mathematical Instruments - The Parabolic Circle, p. 105 , Fig. 5.13 a ( limited preview in Google Book Search [accessed February 9, 2019]).
7. ^ Christian van Randenborgh: Instruments for imparting knowledge in mathematics lessons . Springer Spectrum, Wiesbaden 2015, ISBN 978-3-658-07290-2 , 1.2.1 Van Schooten's circle of parables as a conglomerate of ideas, p. 7th ff ., Fig. 1.2 ( limited preview in Google Book Search [accessed on February 6, 2019]).
8. ^ Christian van Randenborgh: Instruments for imparting knowledge in mathematics lessons . Springer Spectrum, Wiesbaden 2015, ISBN 978-3-658-07290-2 , 1.2.1 The parabolic circle by van Schooten as a conglomerate of ideas, wood replica from 2010, p. 9 ff ., Fig. 1.3 ( limited preview in Google Book Search [accessed on February 6, 2019]).