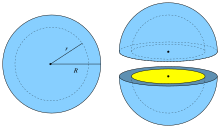
Spherical shell

from Wikipedia, the free encyclopedia
Spherical shell, right: cut open

A spherical shell (also called a hollow sphere ) is the difference between two concentric spheres with different radii .

The plane sections of a spherical shell are circular disks or circular rings .

Volume and surface

If the radii of the two spheres are the volume of the spherical shell

and the surface

.

Shell models of celestial bodies

In the natural sciences spherical shells often used for modeling of inhomogeneous bodies when they approximate sphericity own.

In the case of celestial bodies - which are spherical from a mean diameter of around 500 km - these spherical shells are set in such a way that they have a constant density (mean rock or gas density ). In order for such a celestial body to be in hydrostatic equilibrium , its (spherical) layer surfaces must also be level surfaces .

Some examples are:

In the calculation models, the spherical shells have to meet other conditions that primarily affect pressure and heat transfer . For example, with a star in a stable state, gravity has to keep the radiation and gas pressure in equilibrium everywhere , and the energy that penetrates to the outside must always be the same in the outer spherical shells. Otherwise there would be a build-up of heat and the star would become unstable (see supernova ).

Weightlessness inside a spherical shell

The interior of a spherical shell is weightless . This becomes plausible by breaking it down into symmetrical shell parts, whose gravitational forces cancel each other out

Spherical shells are of particular importance when calculating the gravitational field . In the interior of a hollow spherical shell, the gravity potential is constant because their gravitational forces cancel each other out (see picture). Therefore, if you “lift off” layer by layer from a spherically symmetrical body (eliminated by calculation), the gravitation in the remaining body does not change. The geophysicist Karl Ledersteger calls this the principle of defoliation .

This allows the gravitational field of every larger celestial body to be calculated relatively precisely. However, a complication is due to the rotation and centrifugal force resulting flattening . It is smaller in the interior than near the surface, so that the parallelism of the layers or the density shells is no longer given. Today, however, the corresponding calculations can be carried out using computers by breaking down the bodies into many small elementary bodies.

Galactic rotation

The o. E. Weightlessness inside a spherical shell means in our galaxy that the stars outside of our solar system have no gravitational effect if they are roughly evenly distributed on the different sides of the galaxy. As a result, the Kepler laws no longer apply , for which a single, centrally located mass is the prerequisite. For the actual rotation of the outer Milky Way (around 250 million years in the vicinity of the Sun), the Oort rotation formula was derived a few decades ago . Today, similar spherical shell models can help estimate the extent of dark matter .

Applications in electrical engineering

The special properties of spherical shells are also important when calculating charges and currents . In this way it can be demonstrated that electrical charges are evenly distributed on a conductive spherical surface. In the 18th century, this was the prerequisite for deriving Coulomb's law .

The effect of the Faraday cage can also be proven by a spherical shell model, and the charge and current strength in an electrical conductor in an analogous way.

Further examples

Further examples of spherical shells or hollow spheres are