Soap bubble
A soap bubble is a thin film of soapy water that traps a certain amount of air or other gas to form a hollow sphere that is often iridescent and shimmering. Freshly made soap bubbles show elastic body vibrations, sometimes release water droplets under the effect of gravity, are tolerated or carried by air currents, dry increasingly (if the surrounding air is not saturated with water), become more sensitive to stress from a blast of air or even contact over time with the (dry) surface of another body. Soap bubbles often burst after a short time, sometimes spontaneously.
Keeping soap bubbles in the air and alive for a long time, achieving special figures or size is the subject of artistic handicraft. Soap bubbles are objects of investigation in physics, chemistry and geometry and serve as a clear model for minimal areas .
Soap bubbles can be easily blown by hand or by machine and are used as a stage effect.
Because of this slight transience, 'soap bubble' has become a metaphor for something that is attractive, but nonetheless meaningless and meaningless. This is reflected, for example, in the phrase "The dream burst like a soap bubble" or in the synonym "soap bubble economy " for bubble economy .
In art , at least since the baroque era, the soap bubble has been consistently used iconographically as a vanita symbol and reflects both the beauty and the volatility of human life.
Soap bubbles solve complex spatial problems in mathematics in a physical way , as they form the smallest surface between points and edges in a state of equilibrium .
construction
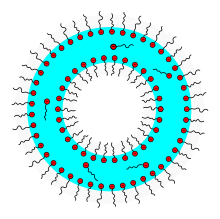
Soap bubbles consist of a thin ( dipolar ) film of water on which soap molecules attach inside and outside with a polar, hydrophilic carboxylate group facing the water and a non-polar, hydrophobic alkyl radical facing away from the water .
The structure is similar to that of biomembranes , but with soap bubbles the water is inside the membrane, not outside.
Why soap bubbles burst
A soap bubble is created when a thin film of water mixes with soap molecules. When inflated, a spherical shape is created. As a result of the gravitational run-off ( drainage ) of the liquid located between the soap film surfaces, a soap bubble increasingly thins in its upper part. You can observe this when you pull a soap film onto the opening of a cup and then hold it vertically. In addition, in the course of the leakage process, soap film-stabilizing surfactant molecules accumulate in the lower area of the soap bubble, so that its upper area is additionally destabilized due to the relative lack of surfactant molecules adsorbed on the surface. In fact, most of the soap bubbles pop in the upper part. Evaporation can be prevented by “locking” the soap bubble or a film of soap in a mason jar . This significantly extends the life of the bladder.
The layer thickness of the soap bubble can be observed: If the surface reflects in colorful interference colors , the layer thickness is comparable to the wavelength of the light. As the layer thickness decreases, the soap skin initially becomes colorless and then dark at the end.
In weightlessness, soap bubbles survive for around one minute, twice as long as on earth. The bladder wall is thicker and more even, and can withstand a pinprick.
Physical basics
Surface tension
The generation of soap bubbles is possible because the surface of a liquid - in this case water - has a surface tension that leads to an elastic behavior of the surface. It is often assumed that the soap is necessary to increase the surface tension of the water. However, the opposite is the case: the surface tension of soapy water is only about a third of that of water. Making soap bubbles with pure water is so difficult because the surface tension is too high, which causes the bubble to burst instantly. In addition, the soap slows down evaporation so that the bubbles last longer. The gas pressure in a soap bubble is higher than the pressure outside, see Young-Laplace equation .
Spherical shape
The surface tension is also the reason for the spherical shape of the soap bubbles. By minimizing the surface, it forces the bubble into this shape, since of all possible shapes for a given volume the sphere has the smallest surface. Without external forces (especially gravity in combination with air friction ) all bubbles would have an ideal spherical shape. Due to their low weight, soap bubbles come very close to this ideal in reality.
Several connected soap bubbles
When two soap bubbles collide, the same principles continue to operate, and the bubbles take on the shape with the smallest surface area. Their common wall bulges into the larger bubble, as a smaller soap bubble has a higher internal pressure. If both soap bubbles are the same size, there is no bulge and the partition is flat.
Plateau's rules state that when several soap bubbles come together, all angles are the same. In a foam with many bubbles, three surfaces always meet at an angle of 120 °. The surface is also minimal here. The same surface tension creates an equilibrium of forces . Four edges meet at an angle of about 109 ° 28 '16 "in a node , also known as a vertex . These rules were established in the nineteenth century on the basis of experimental research by the Belgian physicist Joseph Plateau .
Reflection and interference
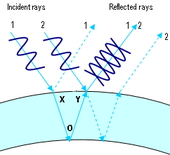
The shimmering colors are created by the interference of light waves on the thin soap skin. The interference leads to the cancellation of part of the color spectrum within a certain viewing angle . The remaining part is perceived in color, as only the complete color spectrum produces white light.
Since the wall of a soap bubble has a certain thickness, incident light is reflected twice - once on each side of the wall (see right). The slightly different path lengths of the two light rays (and special effects on the outer wall, see below) lead to a path difference between them. If the path difference is exactly half a wavelength, the wave troughs of one beam coincide with the wave crests of the other (see second picture). The total is zero, i.e. the corresponding color is deleted. This is called destructive interference, in contrast to constructive interference, in which the two rays are positively superimposed due to a different path difference (third picture).
The actual color of the soap bubble (i.e. the wavelength of the extinguished light or the length of the path difference) depends on the thickness of the soap film and the illumination angle of the surface. The dependence on the layer thickness can be observed when the soap bubble thins out through evaporation. As the thickness decreases, other colors are eliminated. Ultimately, if the thickness of the wall is less than half the smallest wavelength of visible light, no visible light waves cancel each other out and complementary colors can no longer be observed. In this condition, the soap bubble wall is thinner than two ten thousandths of a millimeter. With an even smaller layer thickness one can observe dark spots due to other effects (see below) - it will probably burst in the next moment.
The prerequisite for interference phenomena, the coherence of the wave trains, is fulfilled because of the thinness of the layer. In addition to the different geometric path lengths, another effect also contributes to the path difference:
The wave reflected directly at the air-soap skin interface (point X in the second picture) experiences a phase jump around or while the phase of the transmitted wave remains unchanged even after reflection at the soap skin-air interface (point O in the diagram). There is no phase jump here. The entire path difference is made up of the different path lengths and the phase jump in the reflection at the outer interface.
This also explains the darkening of the bubble in the immediate moment before bursting, when the thickness of the soap skin has decreased to a very small value: This is due to the fact that the transmitted wave, which previously took the longer path through the soap skin, is now practically none covers a longer distance than the direct reflected wave and therefore does not change its phase relative to this. The reflected wave has experienced the phase jump mentioned above, which leads to destructive interference (cancellation) of all waves.
If a soap bubble had the same wall thickness everywhere, the path difference would only be defined by the angle of illumination, and it would show a uniform color gradient. Since the liquid film in a soap bubble, which moves through an air flow, is swirled by air friction, the wall thickness is not homogeneous. Under favorable conditions, these turbulences can be seen with the naked eye. If the soap bubble hovers relatively calmly, however, only a few turbulences occur: You can observe individual, relatively even bands of color. The mostly existing fluctuations in thickness due to the force of gravity are relatively uniform and in principle do not disturb the uniform color gradient.
These colors are easier to make visible in a flat soap film. Such a flat film can e.g. B. be formed in a rectangular or circular frame from thin polymer fibers or thin wire. The optimal conditions for the visibility of the interference colors are indirect lighting (e.g. a sheet of white paper that is illuminated by a halogen lamp) with a 45 degree angle of incidence and observation in reflection at a 45 degree angle of reflection. The background behind the soap film should be dark.
At the edges the film forms a meniscus either with the frame or with a fluid reservoir at the bottom of the film. In the latter case, a combination of gravitation and capillary force is the driving force that causes an inhomogeneous film thickness.
Turbulence and aesthetic moving patterns in the area of the meniscus and at the edges with the frame are caused by hydrodynamic instabilities, in which the Marangoni effect most likely plays an important role.
Frozen soap bubbles
The membrane of a soap bubble can freeze at low temperatures without bursting. This happens with flying soap bubbles at temperatures below −10 ° C outdoors or with adhering soap bubbles in the freezer. They are stable for up to 10 minutes. Sometimes frozen soap bubbles can survive landing on hard and cold surfaces.
The freezing of a soap bubble lying on snow typically occurs through the growth of plumage-like crystals from the adjacent snow, which acts as a germ, and can take about 2 seconds.
use
Shows
Soap bubble shows combine entertainment with artistic performance. A high level of craftsmanship is required, as is perfect soap bubble solutions.
Examples of common performances:
- huge soap bubbles, which often contain objects or people,
- Handling the soap bubbles with bare hands,
- angular soap bubbles in the shape of cubes , tetrahedra , etc.,
- Connect multiple bubbles to more complex structures or sculptures
- Visually appealing effects, for example smoke-filled bubbles or the use of laser light ,
- Soap bubbles filled with helium floating upwards
- Connection of soap bubbles and fire.
Soap bubbles in math
A soap film forms a natural minimal surface . Mathematical research has been focusing on minimal areas since the 19th century. The experiments of the Belgian physicist Joseph Plateau (cf. Plateau problem ) made a significant contribution to this .
An example: As early as 1884, Herrmann Amandus Schwarz proved that a spherical soap bubble has the smallest possible surface area of a certain volume of air. However, it is only in the last few decades that an appropriate language for such problems has been found with the help of geometric measurement theory . In 2000 succeeded Michael Hutchings , Frank Morgan , Manuel Ritoré and Antonio Ros proof that two connected bubbles (a so-called double bubble ) enclosing two different sized volumes of air with the smallest possible surface area (also double bubble theorem ; English double bubble theorem ).
Soap bubbles in architecture
For a long time, soap bubbles were the only means of reliably determining the optimal incline of non-trivial roof structures based on cable systems and supporting arches. For this purpose, the construction was shaped as a frame out of wire and then dipped in soapy water. Careful pulling out resulted in curves that had to be considered the experimentally found optimum of the shape. The result was fixed by photography and other methods and transferred to the associated construction drawings. The respective statics for the given shape could then be determined using other methods. One example of this methodology is the Munich Olympic site .
Toy soap bubbles

One of the earliest artistic depictions of soap bubbles as children's toys can be found in Pieter Bruegel's painting The Children's Games from 1560, which suggests that soap bubbles have been used by children for entertainment for at least 500 years. The mass production of soap began in the 19th century, whereby the soap manufacturer Pears used for marketing in particular John Everett Millais ' painting Soap Bubbles ("Bubbles"), which shows his grandchildren playing with soap bubbles.
In 1948 the chemist Rolf Hein developed a new formula for a detergent, which however had the disadvantage of foaming too much. He had the liquid soap filled into bottles, added a blow ring made of a fine spring wire coil with a handle bent into a ring and sold the product specifically as a children's toy under the brand name Pustefix . Since then, combinations of plastic tubes filled with lye and a blow tube have been mainly used to produce soap bubbles.
literature
- CV Boys : Soap Bubbles. Their colors and the forces which mold them . Dover Publications, New York 1990, ISBN 0-486-20542-8
- Hannelore Dittmar-Ilgen: Why do soap bubbles burst? Physics for the curious . Hirzel-Verlag, Stuttgart 2003, ISBN 3-7776-1149-2
- Cyriel Isenberg: The Science of Soap Films and Soap Bubbles . Tieto Books, Clevedon North Somerset 1978, ISBN 0-905028-02-3
- J. Vogel: Gerthsen Physik . Springer textbook. Springer Verlag, Heidelberg
- CV Boys: Soap bubbles and the forces that form them , nature and knowledge, Volume W 13, Desch, Munich 1961
Web links
Individual evidence
- ↑ science.ORF.at/AFP: Soap bubbles live longer in space. In: science.ORF.at. July 9, 2014, accessed July 9, 2014 .
- ↑ Sam Watons: Researchers test bubble theory in zero gravity, Online at timesnews.net
- ↑ Ashley Leonard: How to Make a Bubble That Doesn't Pop ehow.com, undated, accessed January 24, 2017.
- ↑ Freezing soap bubbles photographed in the snow ... pilleus pulcher, google +, January 23, 2017, accessed January 25, 2017. - Series of images.
- ↑ Michael Hutchings; Frank Morgan; Manuel Ritoré; Antonio Ros: Proof of the double bubble conjecture . In: Announc. Amer. Math. Soc. , 2000, 6 pp. 45-49, pdf .
- ↑ Ansgar Mönter: The one with the soap bubble , from August 17, 2011.
- ^ The story of Pustefix. In: pustefix.de. Retrieved June 6, 2019 .