Euclidean Algorithm

The Euclidean algorithm is an algorithm from the mathematical branch of number theory . It can be used to calculate the greatest common divisor of two natural numbers . The method is named after the Greek mathematician Euclid , who described it in his work " The Elements ".

The greatest common divisor of two numbers can also be determined from their prime factorization . However, if the prime factorization of neither of the two numbers is known, the Euclidean algorithm is the fastest method for calculating the greatest common divisor.

The Euclidean algorithm cannot only be applied to natural numbers. Rather, it can be used to calculate the greatest common divisor of two elements of every Euclidean ring . This includes, for example, polynomials over a body .

The classic algorithm

But if CD does not measure AB, and you take the smaller from the larger alternately with AB, CD, then one number must (finally) remain that measures the previous one.

(From Euclid, The Elements, edited by Clemens Thaer , Wissenschaftliche Buchgesellschaft Darmstadt , VII book, §2)

Example: gcd (44,12) = 4

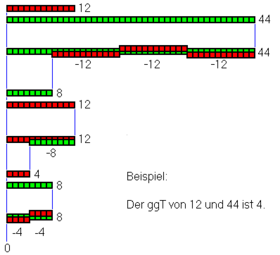
Euclid calculated the greatest common divisor by looking for a common "measure" for the lengths of two lines. To do this, he repeatedly subtracted the smaller of the two lengths from the larger. He takes advantage of the fact that the greatest common divisor of two numbers (or lengths) does not change when you subtract the smaller from the larger.

If the difference between and is very large, many subtraction steps may be necessary. Even before Euclid, Hippasus of Metapontium used this so-called change removal geometrically for the proof of incommensurability in certain regular n-vertices: In the square or in the regular pentagon, for example, there is no common divisor (measure) of a side with the diagonal. ${\displaystyle a}$ ${\displaystyle b}$

Nowadays is used in general, the division algorithm, described below, wherein the steps 2 and 3 are replaced by allowing, in place of the difference and , for the remainder of the division of by decreases. Another advantage of this variant is that it can be applied to any Euclidean rings (for example polynomial rings over a body ) in which the classical algorithm does not work. ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle r}$ ${\displaystyle m}$ ${\displaystyle n}$

Description by pseudocode

The classic algorithm shown here in pseudocode for nonnegative integers a and b:

EUCLID_OLD(a,b)
1  wenn a = 0 dann
3    Ergebnis = b
4  sonst
5    solange b ≠ 0
6      wenn a > b dann
8        a  ${\displaystyle \leftarrow }$ a - b
9      sonst
10       b  ${\displaystyle \leftarrow }$ b - a
11     //
12   //
13   Ergebnis = a
14 //

This algorithm can also be specified in a recursive version:

EUCLID_OLD_RECURSIVE(a,b)
1  wenn b = 0 dann
2    Ergebnis = a
3  sonst
4    wenn a = 0 dann
5      Ergebnis = b
6    sonst
7      wenn a > b dann
8        Ergebnis = EUCLID_OLD_RECURSIVE(a - b, b)
9      sonst
10       Ergebnis = EUCLID_OLD_RECURSIVE(a, b - a)
11     //
12   //
13 //

Modern Euclidean Algorithm

Nowadays, the repeated subtractions of a value that occur in the classic algorithm are replaced by a single division with the remainder . The modern Euclidean algorithm now performs such a division with remainder in every step. It starts with the two numbers and , whose greatest common factor is to be determined. ${\displaystyle a}$ ${\displaystyle b=r_{0}}$

${\displaystyle a=q_{1}\cdot r_{0}+r_{1}}$

In each subsequent step, the divisor and the remainder of the previous step are used to divide again by the remainder, until a division works, that is, the remainder is zero.

${\displaystyle r_{0}=q_{2}\cdot r_{1}+r_{2}}$

${\displaystyle r_{1}=q_{3}\cdot r_{2}+r_{3}}$

${\displaystyle \vdots }$

${\displaystyle r_{n-1}=q_{n+1}\cdot r_{n}+0}$

The divisor of the last division is then the greatest common factor. ${\displaystyle r_{n}}$

${\displaystyle \operatorname {ggT} (a,b)=r_{n}}$

Since the numbers are halved at least in every second step, the process is extremely fast even with large numbers.

example

The greatest common divisor of and is calculated using the Euclidean algorithm as follows: ${\displaystyle \color {MidnightBlue}1071}$ ${\displaystyle \color {OliveGreen}1029}$

${\displaystyle {\begin{array}{rcll}{\color {MidnightBlue}1071}&=&1\cdot {\color {OliveGreen}1029}&+{\color {BurntOrange}42}\\{\color {OliveGreen}1029}&=&24\cdot {\color {BurntOrange}42}&+{\color {OrangeRed}21}\\{\color {BurntOrange}42}&=&2\cdot {\color {OrangeRed}21}&+0\end{array}}}$

The greatest common factor of and is thus . ${\displaystyle \color {MidnightBlue}1071}$ ${\displaystyle \color {OliveGreen}1029}$ ${\displaystyle \color {OrangeRed}21}$

Description by pseudocode

In the following, the modern Euclidean algorithm is described in both a recursive and an iterative variant. Where and are the two numbers whose greatest common divisor is to be calculated. ${\displaystyle a}$ ${\displaystyle b}$

Recursive variant

EUCLID(a,b)
1  wenn b = 0 dann
2    Ergebnis = a
3  sonst
4    Ergebnis = EUCLID(b, Divisionsrest(a durch b))    // siehe Modulo-Funktion
5  //

Iterative variant

EUCLID(a,b)
1  solange b ≠ 0
2      h  ${\displaystyle \leftarrow }$ Divisionsrest(a durch b)        // Siehe Modulo-Funktion
3      a  ${\displaystyle \leftarrow }$ b
4      b  ${\displaystyle \leftarrow }$ h
5  //
6  Ergebnis = a

Correctness of the algorithm

A division with remainder is performed in each step of the algorithm.

${\displaystyle r_{i-1}=q_{i+1}\cdot r_{i}+r_{i+1}\qquad 0\leq r_{i+1}<r_{i}}$

Division by remainder has the property that

${\displaystyle \operatorname {ggT} (r_{i-1},r_{i})=\operatorname {ggT} (r_{i},r_{i+1})}$

applies.

In the last step of the algorithm

${\displaystyle r_{n-1}=q_{n+1}\cdot r_{n}+0}$

is and therefore it applies ${\displaystyle r_{n+1}=0}$

${\displaystyle \operatorname {ggT} (r_{n-1},r_{n})=\operatorname {ggT} (r_{n},0)=r_{n}}$

As in the first step and was is ${\displaystyle r_{i-1}=a}$ ${\displaystyle r_{i}=b}$

${\displaystyle \operatorname {ggT} (a,b)=r_{n}}$

Historical development

Depiction of Euclid by Justus of Ghent (15th century)

The Euclidean algorithm is the oldest known non-trivial algorithm . The procedure was started by Euclid around 300 BC. In his work The elements described. In Book VII (Proposition 1 and 2) he formulated the algorithm for whole numbers and in Book X (Proposition 2 and 3) for real numbers. The latter version is a geometrical algorithm, and Euclid called it anthyphairesis . He was looking for the greatest common "measure" of two routes: a third route, so that the length of the two original routes are a multiple of the length of the third route.

The method was probably not invented by Euclid, as he summarized the findings of earlier mathematicians in the elements. The mathematician and historian Bartel Leendert van der Waerden suspects that Book VII is a textbook on number theory already used by the Pythagoreans . Hippasus of Metapontium led around 500 BC. BC presumably performed his proof of the incommensurability of certain lines and diagonals on the basis of the Euclidean algorithm, and Eudoxus of Knidos (around 375 BC) probably also knew the method. Aristotle (around 330 BC) referred to this method in his work Topik (158b, 29–35).

Centuries later, the Euclidean algorithm was discovered independently in India and China, mainly to solve Diophantine equations from astronomy and to create accurate calendars. In the fifth century, the Indian mathematician and astronomer Aryabhata described the algorithm as a "pulverizer," probably due to its effectiveness in solving Diophantine equations. The Chinese mathematician and astronomer Sun Tzu has already described a special case of the Chinese remainder of the sentence, but the general solution was provided by Qin Jiushao in his book Shushu Jiuzhang ( Chinese  數 書 九章  /  数 书 九章  - "Mathematical Treatise in Nine Chapters" ) released. In modern Europe, the Euclidean algorithm was described again for the first time in the second edition of Bachets Problèmes plaisants et délectables, qui se font par les nombres . The algorithm was used in Europe to solve Diophantine equations and to calculate the continued fraction expansion. Nicholas Saunderson published the extended Euclidean algorithm and attributed it to Roger Cotes as a method for the efficient computation of continued fractions.

In the 19th century, the Euclidean algorithm gave the impetus to the development of new number systems such as the Gaussian numbers and the Eisenstein numbers . In 1815 Carl Friedrich Gauss used the Euclidean algorithm to show the unambiguous factoring of the Gaussian numbers. However, his work was not published until 1832. Gauss also mentioned the algorithm in his Disquisitiones Arithmeticae published in 1801 , but only as a method for calculating continued fractions. Peter Gustav Lejeune Dirichlet seems to be the first to describe the Euclidean algorithm as the basis of a large part of number theory. He noted that many of the results of number theory, such as unique factorization, also apply to other number systems in which the Euclidean algorithm can be applied. Dirichlet's lectures on number theory were edited and expanded upon by Richard Dedekind , who used the Euclidean algorithm for studying algebraic numbers , a new, more general type of number. For example, Dedekind was the first to prove Pierre de Fermat's two-squares theorem by clearly factoring the Gaussian numbers. Dedekind introduced the concept of the Euclidean ring , a number system in which a generalized variant of the Euclidean algorithm can be applied. In the last decades of the 19th century, the Euclidean algorithm gradually stepped back from Dedekind's more general theory of ideals .

In 1829, Jacques Charles François Sturm developed the Sturm chains to calculate the number of zeros of a polynomial in a given interval. A variant of the Euclidean algorithm is used to determine the individual links in a chain.

In the past, there have been countless attempts to generalize the Euclidean algorithm to more than two natural numbers, for example in order to find, in addition to their greatest common divisor, also optimal (roughly the smallest possible) multipliers which, in linear combination with the numbers, provide this divisor. The modern state of research on this was presented by Havas, Majewski and Matthews.

The Euclidean algorithm was the first algorithm to compute integer relationships of commensurable real numbers. In recent years, further algorithms have been developed for this task, for example the Ferguson – Forcade algorithm from 1979 and related algorithms, the LLL algorithm , the HJLS algorithm (after the authors H åstad , J ust , L agarias and S chnorr ) and the PSLQ algorithm (after partial sum of squares plus LQ matrix decomposition ). In 2001 it was shown that the instability of the HJLS algorithm reported by some authors was merely due to an inexpedient implementation and that this algorithm is equivalent to the PSLQ algorithm. Its multidimensional generalizations by George Szekeres (1970), Helaman Ferguson and Rodney Forcade (1981), Just (1992), von Rössner and Schnorr (1996) and the very general approach by Lagarias (1994) are based more closely on the actual Euclidean algorithm .

In 1969, Cole and Davie developed the two-player game "Euclid", which is based on the Euclidean algorithm. There is an optimal strategy in this game. The two players start with two stacks of and stones. In each round a player takes -x as many stones from the larger pile as the smaller pile is. In this way the next player can reduce the larger pile of stones to stones, where the size of the smaller pile is. The player who completely removes a stack wins. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle m}$ ${\displaystyle x}$ ${\displaystyle x-my}$ ${\displaystyle y}$

Runtime analysis

Number of steps to calculate GCD ( x , y ). Red points mean few steps, yellow, green and blue points relatively more steps. The dark blue line has the gradient Φ, where Φ is the golden ratio .

With the Euclidean algorithm, the GCF can be calculated with relatively little effort (compared to calculating the prime factorization of the numbers a and  b ). The runtime analysis shows that the worst case of input is two consecutive Fibonacci numbers . With consecutive Fibonacci numbers, the remainder is always the next smaller Fibonacci number. In the worst case, the number of divisions required is Θ (log ( ab )), where log ( ab ) is proportional to the number of digits in the input (see Landau symbols ) .

Since the time required to divide two numbers depends on the number of digits in the numbers, the actual running time is O ( log (ab) ^ 3 ) if the division is carried out naively. Due to the complete transfer of the actual calculation into the frequency domain by means of a special fast Fourier transformation , as it is used in the Schönhage-Strassen algorithm , faster reciprocal value calculation with the Newton method (in the frequency domain) for division and subsequent reverse transformation using inverse fast Fourier Transformation one arrives at a theoretical lower limit of Ω ( n⋅ log ( n )), where n is the maximum number of digits of a and b .

The variant of the Euclidean algorithm developed by Schönhage could be further accelerated by parallelization on a multi-processor system.

Asymptotic estimates are available for the number of steps, where Porter's constant plays a role.

Euclidean algorithm and continued fraction decomposition

The quotients that appear in the Euclidean algorithm are exactly the part denominators that appear in the continued fraction of . Here for the above example with highlighted digits: ${\displaystyle {\frac {a}{b}}}$

1071	= 1	× 1029	+ 42
1029	= 24	× 42	+ 21
42	= 2	× 21	+ 0

The continued fraction can be developed from this:

${\displaystyle {\frac {1071}{1029}}=\mathbf {1} +{\frac {42}{1029}}=\mathbf {1} +{\frac {1}{\frac {1029}{42}}}=\mathbf {1} +{\frac {1}{\mathbf {24} +{\frac {21}{42}}}}=\mathbf {1} +{\frac {1}{\mathbf {24} +{\frac {1}{\mathbf {2} }}}}=[1;24,2]}$.

This procedure can also be used for any real number . If it is not rational, the algorithm just never ends. The resulting sequence of quotients then represents the infinite continued fraction of . ${\displaystyle r}$ ${\displaystyle r}$ ${\displaystyle r}$

Other number systems

As described above, the Euclidean algorithm is used to calculate the greatest common divisor of two natural numbers. The algorithm can, however, also be generalized to real numbers and more exotic number systems such as polynomials , quadratic numbers and the non-commutative Hurwitz quaternions. In the latter case, the Euclidean algorithm is used to show the important property of a unique factorization. This means that such a number can be uniquely broken down into irreducible elements , the generalization of prime numbers. Unique factorization is fundamental to many proofs of number theory.

Rational and real numbers

As already described by Euclid in book 10 of his work "The Elements", the Euclidean algorithm can also be applied to real numbers. The goal of the algorithm is then to find a real number such that the two are numbers and integer multiples of that number. This task is synonymous with the search for an integer relationship between the two real numbers and , i.e. the calculation of two integers and , for which applies. Euclid used this algorithm when considering the incommensurability of routes. ${\displaystyle g}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle s}$ ${\displaystyle t}$ ${\displaystyle sa+tb=0}$

The Euclidean algorithm for real numbers differs in two ways from its counterpart for integers. For one, the remainder is a real number, even though the quotients are still integers. On the other hand, the algorithm does not always end after a finite number of steps. However, if he does so, then the fraction is a rational number; so there are two whole numbers and with ${\displaystyle r_{k}}$ ${\displaystyle q_{k}}$ ${\displaystyle {\tfrac {a}{b}}}$ ${\displaystyle m}$ ${\displaystyle n}$

${\displaystyle {\frac {a}{b}}={\frac {mg}{ng}}={\frac {m}{n}}}$

and can be written as a continued fraction . If the algorithm doesn't end, then the fraction is an irrational number and is identical to the infinite continued fraction . Examples of infinite continued fractions are the golden number and the square root of 2 . In general, the algorithm is unlikely to stop because almost all ratios of two real numbers are irrational numbers. ${\displaystyle [q_{0};q_{1},q_{2},\ldots ,q_{N}]}$ ${\displaystyle {\tfrac {a}{b}}}$ ${\displaystyle [q_{0};q_{1},q_{2},\ldots ]}$ ${\displaystyle \Phi =[1;1,1,\ldots ]}$ ${\displaystyle {\sqrt {2}}=[1;2,2,\ldots ]}$ ${\displaystyle {\tfrac {a}{b}}}$

Polynomials

Polynomials in a variable over a body form a Euclidean ring . The polynomial division is for these polynomials a division with remainder and the Euclidean algorithm can be carried out in the same way as with the whole numbers. The calculation of the greatest common divisor of the polynomials and in is , for example, as follows: ${\displaystyle f=x^{4}+x^{3}+x+1}$ ${\displaystyle g=x^{2}-1}$ ${\displaystyle \mathbb {R} [x]}$

${\displaystyle x^{4}+x^{3}+x+1=\left(x^{2}+x+1\right)\cdot \left(x^{2}-1\right)+\left(2x+2\right)}$

${\displaystyle x^{2}-1=\left({\frac {1}{2}}x-{\frac {1}{2}}\right)\cdot (2x+2)+0}$

Therewith (or the associated polynomial ) is a greatest common divisor of and . ${\displaystyle 2x+2}$ ${\displaystyle x+1}$ ${\displaystyle f}$ ${\displaystyle g}$

Polynomials with coefficients from a factorial ring

We hold a factorial ring (i.e. a ring with prime factorization that is unique except for units) and consider polynomials from the polynomial ring , i.e. polynomials in a variable with coefficients . In the special case , where a body, we get the ring of polynomials in two variables over . ${\displaystyle R}$ ${\displaystyle R[x]}$ ${\displaystyle x}$ ${\displaystyle R}$ ${\displaystyle R=k[y]}$ ${\displaystyle k}$ ${\displaystyle k[x,y]}$ ${\displaystyle k}$

In , division with remainder is no longer generally feasible. Z. B. and in . Polynomial division in returns the quotient that is not in . However, we can define a pseudodivision as follows: Let and polynomials off with degree or , let be the leading coefficient of the polynomial , and . Then there are polynomials such that ${\displaystyle R[x]}$ ${\displaystyle f=x^{2}+1}$ ${\displaystyle g=2x+1}$ ${\displaystyle \mathbb {Z} [x]}$ ${\displaystyle \mathbb {Q} [x]}$ ${\displaystyle {\frac {1}{2}}x-{\frac {1}{4}}}$ ${\displaystyle \mathbb {Z} [x]}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle R[x]}$ ${\displaystyle d_{f}}$ ${\displaystyle d_{g}}$ ${\displaystyle g_{0}}$ ${\displaystyle g}$ ${\displaystyle \delta :=d_{f}-d_{g}}$ ${\displaystyle q,r\in R[x]}$

${\displaystyle g_{0}^{\delta +1}f=qg+r,}$

again being of a lesser degree than . The GCF of and can be determined by repeating the pseudodivision , but the procedure is inefficient in practice, since the factors cause the coefficients of the intermediate results to grow exponentially. To avoid this, the content of the remainder can be removed after each step , which in turn requires GCF calculations in . The GCF can be calculated more efficiently with the sub-resultant method. ${\displaystyle r}$ ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle g_{0}^{\delta +1}}$ ${\displaystyle r}$ ${\displaystyle R}$

variants

Stein's algorithm , named after him, comes from Josef Stein and works without the complex divisions. He only uses divisions by two, which can be performed very quickly by a computer. For this reason, this algorithm is also called the binary Euclidean algorithm. The performance advantage on real computers only becomes apparent when the integer type exceeds the register width of the processor.

If you remember the quotients of the intermediate steps with the Euclidean algorithm , then a representation can be made ${\displaystyle q_{i}}$

${\displaystyle \operatorname {ggT} (a,b)=sa+tb}$

with whole numbers and find. This is called the extended Euclidean algorithm . With this, the inverses can be calculated in residual class rings . ${\displaystyle s}$ ${\displaystyle t}$

Another extension is the algorithm behind the law of square reciprocity . With this the Jacobi symbol can be calculated efficiently.

Web links

Wikibooks: Algorithm collection for the Euclidean algorithm  - learning and teaching materials

• Christian Spannagel : The Euclidean Algorithm . Lecture series, 2012.

Individual evidence

1. ↑ Bartel Leendert van der Waerden : Awakening Science. Egyptian, Babylonian and Greek mathematics . Birkhäuser Verlag, Basel 1956, p. 188 .
2. ^ Donald E. Knuth : The Art of Computer Programming . 3. Edition. tape 2 : Seminumerical Algorithms . Addison-Wesley Professional, 1997, ISBN 0-201-89684-2 , pp. 334-337 .
3. ^ ^{A b} John Stillwell : Elements of Number Theory . Springer-Verlag, 2003, ISBN 0-387-95587-9 , p. 41-42 .
4. ↑ ^{a b c d} James Joseph Tattersall: Elementary number theory in nine chapters . Cambridge University Press, 2005, ISBN 978-0-521-85014-8 , pp. 70-72 .
5. ↑ Kenneth H. Rosen, Bart Goddard: Elementary Number Theory and Its Applications . 2000, ISBN 0-201-87073-8 , pp. 86-87 .
6. ↑ Øystein Ore : Number Theory and Its History . McGraw – Hill, New York 1948, p. 247-248 .
7. ↑ James Joseph Tattersall: Elementary number theory in nine chapters . Cambridge University Press, 2005, ISBN 978-0-521-85014-8 , pp. 72, 184-185 .
8. ^ Carl Friedrich Gauß : Theoria residuorum biquadraticorum .
9. ^ ^{A b} John Stillwell: Elements of Number Theory . Springer-Verlag, 2003, ISBN 0-387-95587-9 , p. 31-32 .
10. ^ Peter Gustav Lejeune Dirichlet & Richard Dedekind : Lectures on number theory . 2nd Edition. Friedrich Vieweg and son, Braunschweig 1871, p. 30-31 ( gdz.sub.uni-goettingen.de ).
11. ↑ Peter Gustav Lejeune Dirichlet, Richard Dedekind: Lectures on number theory . 4th edition. Friedrich Vieweg and Son, Braunschweig 1894, Supplement XI.
12. ↑ see for example: George Havas, Bohdan S. Majewski, Keith R. Matthews: Extended GCD algorithms ( Memento of the original from March 5, 2014 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF, 160 kB). Technical Report TR0302, The University of Queensland, Brisbane 1994. or G. Havas, BS Majewski, KR Matthews: Extended GCD and Hermite normal form algorithms via lattice basis reduction ( Memento of the original from March 5, 2014 in the Internet Archive ) Info: Der Archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF, 266 kB). Experimental Mathematics 7 (1998) No. 2, pp. 125-136 and the extensive bibliography therein  
13. ↑ Eric W. Weisstein : Integer Relation . In: MathWorld (English).
14. ^ Alan Meichsner: Integer relation algorithms and the recognition of numerical constants. Master's thesis, Simon Fraser University, June 2001.
15. ↑ George Szekeres: Multidimensional continued fractions. Ann. Univ. Sci. Budapest. Sectio Math. 13 (1970), pp. 113-140
16. ^ Helaman RP Ferguson, Rodney W. Forcade: Multidimensional Euclidean algorithms. J. Reine Angew. Math. 334 (1982) pp. 171-181
17. ↑ Bettina Just: Generalizing the continued fraction algorithm to arbitrary dimensions. SIAM J. Comput. 21: 909-926 (1992)
18. ↑ Carsten Rössner, Claus-Peter Schnorr: An optimal, stable continued fraction algorithm for arbitrary dimension. Electronic Colloquium on Computational Complexity, ECCC-TR96-020
    Carsten Rössner, Claus-Peter Schnorr: An optimal, stable continued fraction algorithm. In: Lecture Notes Computer Science 1084, Springer 1996, pp. 31-43
19. ↑ Jeffrey Lagarias: Geodesic multidimensional continued fractions. Proc. London Math. Soc. 69 (1994) pp. 464-488
20. ^ AJ Cole, AJT Davie: A game based on the Euclidean algorithm and a winning strategy for it . In: Mathematica Gazette . tape 53 , 1969, p. 354-357 , doi : 10.2307 / 3612461 .
21. ^ EL Spitznagel: Properties of a game based on Euclid's algorithm . In: Mathematical Magazine . tape 46 , 1973, p. 87-92 .
22. ↑ Joe Roberts: Elementary Number Theory: A Problem Oriented Approach . MIT Press, Cambridge, MA 1977, ISBN 0-262-68028-9 , pp. 1-8 .
23. ^ Giovanni Cesari: Parallel implementation of Schönhage's integer GCD algorithm . In: ANTS-III (Lecture Notes Computer Science) . tape 1423 . Springer-Verlag, 1998, p. 64-76 .