Collapsing circle

The collapsing compass , also called Euclidean compass or folding compass , is a compass that snaps shut when you lift it from the sheet. This is usually a theoretical consideration because most circles do not collapse.

Euclid uses collapsing compasses in his geometry. In Proposition 2 of Book I of the Elements , he proves how you can still transfer any distance with such a compass and a ruler, i.e. the equivalence of the construction with a ruler and collapsing and non-collapsing compasses.

Problem definition and definition of terms

For constructions with compasses and ruler , a non-collapsing compass is usually used. In the original construction problems of Euclid, however, a collapsing compass was assumed, the radius of which cannot be fixed when lifting from the sheet in order to draw another circle with this radius.

Note that a collapsing circle is a mathematical consideration. According to Euclid, there is always a straight line (which can be constructed with a ruler) for two points A and B, which runs through both points, as well as two circles, one around A and one around B, with the radius of the line from A to B.

This gives you almost all possible constructions that can be made with a pair of compasses and a ruler, except for taking a segment AB with a pair of compasses and drawing a circle with this radius around a third point C.

A collapsing circle is a circle that can be used to draw a circle. However, after the circle has been drawn, the set radius collapses: the compass snaps together so that you cannot set the compass on another point and draw a circle with the same radius - unless a point already exists that corresponds to the new one Point already has this distance.

In fact, the result is that further steps with a collapsing compass and a ruler can also be used to construct circles that can be drawn around a third point using the radius as the distance between two points. See below for proof.

Mathematical explanation for constructions with compasses and ruler

Let be a set of points im , the set of all straight lines im that pass through at least two points , the set of all circles whose centers are the points from and whose radii are equal to the distances between two points from . ${\displaystyle \mathrm {\mathrm {M} } }$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathrm {G(\mathrm {M} )} }$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathrm {\mathrm {M} } }$ ${\displaystyle \mathrm {K(\mathrm {M} )} }$ ${\displaystyle \mathrm {\mathrm {M} } }$ ${\displaystyle \mathrm {\mathrm {M} } }$

Then is the set of all points that can be constructed from constructions with compasses and ruler using the following operations: ${\displaystyle {\hat {M}}}$ ${\displaystyle \mathrm {\mathrm {M} } }$

1. Section of two different straight lines ${\displaystyle \mathrm {G} (\mathrm {M} )}$
2. Cut a straight line out with a circle out ${\displaystyle \mathrm {G} (\mathrm {M} )}$ ${\displaystyle \mathrm {K} (\mathrm {M} )}$
3. Cut out two different circles ${\displaystyle \mathrm {K} (\mathrm {M} )}$

It makes no difference whether you work with a collapsing or a non-collapsing compass, because all points that can be constructed using a non-collapsing compass can also be constructed with a collapsing compass. Proof see construction below. ${\displaystyle {\hat {M}}}$ ${\displaystyle {\hat {M}}}$

However: Let now be the set of all points that can be constructed from M by constructions with a collapsing compass and ruler and the set of all points that can be constructed from M by constructions with a non-collapsing compass and ruler in just one step . ${\displaystyle M^{\prime }}$ ${\displaystyle {\tilde {M}}}$

Then the following applies: because even for a three-element set of points A, B, C the intersection of a straight line through A and B with a circle with a radius around C is in , but not in . The construction of this circle around C requires a few more steps with a collapsing circle (see below). ${\displaystyle {\tilde {M}}\not =M'}$ ${\displaystyle \mathrm {M} }$ ${\displaystyle \mid {\overline {AB}}\mid }$ ${\displaystyle {\tilde {M}}}$ ${\displaystyle M^{\prime }}$

Constructing a circle around a point with a distance between two points other than radius with a collapsing circle

In order to show that the same points can be constructed with a collapsing compass and a ruler as with a non-collapsing compass and a ruler, it suffices to show that with a collapsing compass and ruler the construction of a circle around a point with a distance between two other points as a radius is possible. Sections from such a circle with a straight line or with another (possibly similar) circle are then easily possible, since both circles (or the circle and the straight line) can already be constructed, i.e. their cuts accordingly.

proof

(1) Initial situation		(2) Point D. ${\displaystyle a}$

(1) There are three points A, B, C. In the drawing, the straight lines through A and B as well as through A and C are already drawn. The straight line through B and C is not required. ${\displaystyle a}$ ${\displaystyle b}$

The aim is to construct a circle around C with the length of the path as a radius , in order to create an intersection with the straight line . ${\displaystyle \mid {\overline {AB}}\mid }$ ${\displaystyle b}$

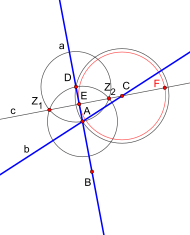
For this, two parallels must be formed, one for each of the two existing straight lines. The first parallel (to ) should go through point C, and the second parallel (to ) should go through point B. ${\displaystyle d}$ ${\displaystyle a}$ ${\displaystyle e}$ ${\displaystyle b}$

(2) To construct the first of these parallels, a circle with a radius is drawn around point C. This intersects the straight line in A and another point D. (If it is perpendicular to , is natural . In this case, the next step can be omitted and A can be used directly as the point E to be determined in this step.) ${\displaystyle \mid {\overline {AC}}\mid }$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle A=D}$

(3) Point E. ${\displaystyle a}$		(4) Point F on ${\displaystyle c}$

(3) Now a circle with a radius is drawn around A and around D and the points of intersection of these two circles (here Z ₁ and Z ₂ ) are connected to form a straight line . The straight line is a perpendicular from C to , i.e. H. a straight line through C. that is too perpendicular. H. the intersection of with is denoted as E. ${\displaystyle \mid {\overline {AD}}\mid }$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle c}$ ${\displaystyle a}$

(4) This is followed by determining the point on this perpendicular F at the same distance as E C by a circle with radius C is pulled. ${\displaystyle c}$ ${\displaystyle \mid {\overline {CE}}\mid }$

(5) parallel ${\displaystyle d||a}$		(6) parallel ${\displaystyle e||b}$

(5) With the help of E and F, two circles with a radius can be drawn that intersect at two points (here G and H). These two points define a perpendicular to the perpendicular ( ) to (i.e. a parallel to ) that runs through point C. This parallel is called. Thus the first parallel is constructed. The parallel to can be constructed in the same way . This gives a parallelogram and the intersection point K of the two parallels and . ${\displaystyle \mid {\overline {EF}}\mid }$ ${\displaystyle c}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle d}$ ${\displaystyle e}$ ${\displaystyle b}$ ${\displaystyle d}$ ${\displaystyle e}$

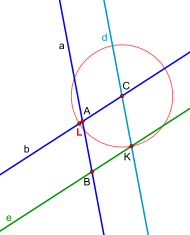
(6) For a better overview, the two constructions of the parallels are divided into two pictures.

(7) parallelogram and ${\displaystyle a||d}$ ${\displaystyle b||e}$		(8) Result: point L

(7) The distance is obviously as long as . ${\displaystyle {\overline {CK}}}$ ${\displaystyle {\overline {AB}}}$

(8) Now only a circle with a radius around C has to be drawn. This cuts . Intersection L is the point we are looking for. ${\displaystyle \mid {\overline {CK}}\mid }$ ${\displaystyle b}$

annotation

The proof assumes that C is not on . In such a case, the method described can be used to draw a circle with the radius around any point P that is not on (i.e., P is used instead of C in the construction above). During the construction, a straight line is created (analogous to the construction above) that goes through P and is too parallel. The constructed circle intersects at two points Q and R (analogous to K in the construction above), whereby it obviously holds that . ${\displaystyle a}$ ${\displaystyle \mid {\overline {AB}}\mid }$ ${\displaystyle a}$ ${\displaystyle p}$ ${\displaystyle d}$ ${\displaystyle a}$ ${\displaystyle p}$ ${\displaystyle \mid {\overline {PQ}}\mid =\mid {\overline {PR}}\mid =\mid {\overline {AB}}\mid }$

This allows the construction to be performed a second time, using the length of one of these two lines as the radius for the circle around C (i.e., now P and Q are used as A and B in the construction above). Since and are parallel and since C is on , but P is not, C is not on either , so the construction works now. In addition, the construction of a parallel to in the subsequent construction can obviously be skipped. ${\displaystyle a}$ ${\displaystyle p}$ ${\displaystyle a}$ ${\displaystyle p}$ ${\displaystyle p}$

literature

• C. Bessenrodt: Algebra I, winter semester 2003/2004 - point 1.1 - lecture notes (PDF; 1.0 MB)
• Robin Hartshorne : Euclid and Beyond 1. Euclid's Geometry Springer-Verlag New York, Inc. in 2000; 2 Ruler and Compass Constructions, page 18.

Web links

• Collapsing circle, proof using an alternative solution

Individual evidence

1. ↑ Knut Smoczyk: Geometrie für das Lehramt , Norderstedt: Books on Demand, 2019, page 221, 7.1. Euclidean tools; (Online copy (BoD)) ISBN 978-3-7481-6616-0 ; accessed on March 25, 2019.
2. ↑ Heinz Lüneburg: Of numbers and sizes. Volume 2. Birkhäuser, ISBN 978-3-7643-8778-5 , page 336.
3. ^ ^{A b} William Dunham : Mathematics from A – Z: An alphabetical tour through four millennia , Springer Basel AG, Greek Geometry, page 103 ff .; accessed on December 30, 2018.