Manhattan metric

The lines in red, blue and yellow are three examples of the Manhattan distance between the two black dots (each 12 units long); the green line represents the Euclidean distance for comparison , which has a length of units. ${\displaystyle 6{\sqrt {2}}\approx 8.5}$

The Manhattan metric (also Manhattan distance , Mannheim metric , taxi or city ​​block metric ) is a metric in which the distance between two points and as the sum of the absolute differences between their individual coordinates is defined: ${\displaystyle d}$ ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle d(a,b)=\sum _{i}\left|a_{i}-b_{i}\right|}$

The underlying geometry was first examined by Hermann Minkowski .

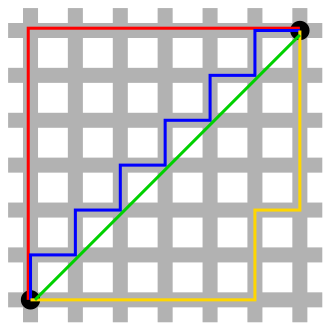
This distance definition gets its name from the checkerboard-like arrangement of the building blocks and the orthogonal street grid of Manhattan , which force a taxi driver to overcome the distance between two addresses by lining up “vertical” and “horizontal” stretches of road. The inner city of Mannheim has a comparable structure.

A taxi driver who plans his route using such a system always covers the same distance on the journey to his destination, provided he only uses routes that bring him closer to his destination. In doing so, it never leaves a rectangle aligned with the grid, the opposite corners of which lie on the start and destination points.

The Manhattan metric is the metric generated by the sum norm (1 norm) of a vector space.

For example, in the graphic opposite, the Manhattan metric is in a two-dimensional space, so that

${\displaystyle d(a,b)=|a_{1}-b_{1}|+|a_{2}-b_{2}|=|6|+|6|=12}$

where and are the points marked in black. ${\displaystyle a=(a_{1},a_{2})}$ ${\displaystyle b=(b_{1},b_{2})}$

See also

• French railway metric

Web links

• Eric W. Weisstein : Taxicab Metric . In: MathWorld (English).

Individual evidence

1. ↑ Christian Royer: Simultaneous optimization of production locations, production quantities and distribution areas . Utz, Wiss., Munich 2001, ISBN 3-8316-0042-2 , p. 55 .