Initial topology

As initial topology with respect to an imaging family is known in the topology , the coarsest topology on a set that this family of mappings from other topological spaces constantly makes. The initial topology is thus created by "backward transferring" the topological structures present in the image spaces to the crowd . This is the application of a more general concept from category theory to topological spaces, with which important “natural spaces” such as product and sub-spaces can be placed in a common framework. ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle X}$

definition

Given is a set , a family of topological spaces and a family of mappings of into the spaces . A topology on is called an initial topology with respect to the family if it has one of the following three equivalent properties: ${\displaystyle X}$ ${\displaystyle (Y_{i},T_{i})}$ ${\displaystyle f_{i}\colon X\to Y_{i}}$ ${\displaystyle X}$ ${\displaystyle Y_{i}}$ ${\displaystyle S}$ ${\displaystyle X}$ ${\displaystyle (Y_{i},T_{i},f_{i})}$

1. ${\displaystyle S}$is the coarsest topology with respect to which all mappings are continuous. ${\displaystyle X}$ ${\displaystyle f_{i}}$
2. The archetypes of all open sets under all mappings of the family form a sub-basis of the topology . ${\displaystyle f_{i}^{-1}(O),\;(O\in T_{i})}$ ${\displaystyle S}$
3. A function from a topological space in is continuous if and only if is continuous for each . ${\displaystyle g}$ ${\displaystyle Z}$ ${\displaystyle X}$ ${\displaystyle f_{i}\circ g}$ ${\displaystyle i\in I}$

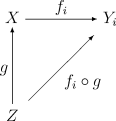
Note that the diagram is not a universal property.

Remarks

The three formulations of the definition illuminate different aspects of the initial topology:

1. Here it is viewed as the smallest upper bound of certain topologies in the association of all topologies . Each individual image pulls back a topological structure from its image space and the initial topology is the coarsest topology that contains all these topologies, i.e. the product of the union of these topologies. With this definition the existence of the initial topology can be proven. ${\displaystyle X}$ ${\displaystyle f_{i}}$ ${\displaystyle S_{i}}$ ${\displaystyle X}$ ${\displaystyle S}$
2. This definition is constructive. It can be used to generate any open sets of the initial topology, see Basis (topology) . Since a topology is uniquely determined by a sub-base, the uniqueness of the initial topology easily follows from this definition .
3. The abstract characterization justifies the designation “initial” topology and allows these structures to be viewed in the more general framework of category theory. The final topology can be characterized by its dual property.

Examples

Some frequently used constructions of topological spaces can be understood as initial topologies:

• The subspace topology is the initial topology on the subset with respect to the natural inclusion mapping.
• The product topology is the initial topology with regard to the natural projections onto the factor spaces.
• The weak topology on a standardized vector space is the initial topology with regard to the continuous linear forms on (i.e. the topological dual space of ). ${\displaystyle E}$ ${\displaystyle E}$ ${\displaystyle E'}$ ${\displaystyle E}$
• If a family of topologies is given on a set , then the initial topology with regard to the identity (the coarsest topology that makes the identical mapping from to continuous in all topologies) is precisely the smallest upper bound of the family in the association of topologies to . ${\displaystyle X}$ ${\displaystyle T_{i}}$ ${\displaystyle X}$ ${\displaystyle (X,T_{i})}$ ${\displaystyle (T_{i})}$ ${\displaystyle X}$

Categorical description

The above universal property cannot easily be expressed within the category of topological spaces, since in it one can only talk about continuous functions between topological spaces and not about sets and arbitrary functions between them (unless one identifies a set with the discrete topology on it or similar). However, it can be characterized when a topological space carries the initial topology with respect to a family of continuous mappings from this space. So be an object in Top and a family of morphisms. then carries the initial topology with regard to that if every bimorphism with morphisms that satisfy is an isomorphism : Because such a bimorphism corresponds to a bijective continuous mapping, i.e. a (not necessarily real) coarsening, and if the coarsest topology is already present, which is compatible with the maps, such coarsening must be an isomorphism (ie a homeomorphism ). For a one-element family, whose element is a monomorphism , this condition corresponds precisely to the condition for an extreme monomorphism; it immediately follows that the extreme monomorphisms are the topological embeddings . ${\displaystyle X}$ ${\displaystyle f_{i}\colon X\to Y_{i}}$ ${\displaystyle X}$ ${\displaystyle f_{i}}$ ${\displaystyle g\colon X\to Z}$ ${\displaystyle h_{i}\colon Z\to Y_{i}}$ ${\displaystyle f_{i}=h_{i}g}$

If, on the other hand, you want to define the initial topology for a family of not necessarily continuous functions, you have to take the detour via the category of sets and relate them to Top using the forget function .

literature

• Boto von Querenburg : Set theoretical topology (= Springer textbook ). 3rd, revised and expanded edition. Springer-Verlag, Berlin a. a. 2001, ISBN 3-540-67790-9 .
• Eraldo Giuli (Ed.): Categorical Topology. Proceedings of the L'Aquila Conference (1994). Kluwer Academic, Dordrecht u. a. 1996, ISBN 0-7923-4049-3 .
• Harro Heuser : Functional Analysis. Theory and application (= mathematical guidelines ). 3rd, revised edition. Teubner-Verlag, Stuttgart 1992, ISBN 3-519-22206-X .