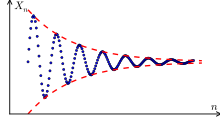
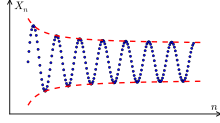
Cauchy episode

Example of a Cauchy sequence: the distance between the terms of the sequence becomes arbitrarily small in the course of the sequence.

Example of a sequence that is not a Cauchy sequence: the distance between the terms of the sequence does not become arbitrarily small in the course of the sequence.

A Cauchy sequence (or Cauchy sequence ), Cauchy sequence or fundamental sequence is a sequence in mathematics in which the distance between the terms of the sequence becomes arbitrarily small in the course of the sequence. Cauchy sequences are named after the French mathematician Augustin-Louis Cauchy and are of fundamental importance for the structure of analysis .

The limit of a Cauchy sequence of real numbers is always a real number. The limit of a Cauchy sequence of rational numbers can also be an irrational number . In general all Cauchy sequences of elements of a metric space converge if and only if the space is complete . Each incomplete metric space, by the formation of equivalence classes of Cauchy sequences completed be.

Cauchy sequences of numbers

definition

A sequence of rational or real numbers is called a Cauchy sequence or fundamental sequence if there is an index for each , so that from this index onwards all sequence members are less than apart from one another. This condition can be formally expressed as ${\displaystyle (a_{i})_{i\in \mathbb {N} }}$ ${\displaystyle \varepsilon >0}$ ${\displaystyle N}$ ${\displaystyle \varepsilon }$

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad \left|a_{m}-a_{n}\right|<\varepsilon }$

write, where represents the amount of a number. ${\displaystyle |\cdot |}$

Remarks

• In the definition, by and also by can be replaced. ${\displaystyle \geq N}$ ${\displaystyle >N}$ ${\displaystyle <\varepsilon }$ ${\displaystyle \leq \varepsilon }$

• Equivalent to this definition, one can also demand that for every positive number, no matter how small, there is an interval of length in which almost all of the elements of the sequence lie. ${\displaystyle \varepsilon }$ ${\displaystyle 2\varepsilon }$

• This definition largely corresponds to the definition for convergent sequences, but without using the concept of the limit value of a sequence. Cauchy sequences were therefore also previously referred to as "self-convergent sequences" or "concentrated sequences".

Examples

• The episode is a Cauchy episode. Namely, for any given one, one can choose one that is fulfilled. If arbitrarily chosen, then applies ${\displaystyle a_{i}={\tfrac {1}{i}}}$ ${\displaystyle \varepsilon >0}$ ${\displaystyle N}$ ${\displaystyle N>{\tfrac {1}{\varepsilon }}}$ ${\displaystyle n\geq m>N}$

${\displaystyle |a_{m}-a_{n}|=\left|{\frac {1}{m}}-{\frac {1}{n}}\right|=\left|{\frac {n-m}{mn}}\right|<{\frac {n}{mn}}={\frac {1}{m}}<{\frac {1}{N}}<\varepsilon }$.

• The episode is not a Cauchy episode. Be chosen and any natural number. Then you can and choose and it still applies ${\displaystyle a_{i}=i}$ ${\displaystyle \varepsilon ={\tfrac {1}{2}}}$ ${\displaystyle N}$ ${\displaystyle n=N+1}$ ${\displaystyle m=n+1}$

${\displaystyle |a_{m}-a_{n}|=|m-n|=1\geq \varepsilon }$.

completeness

There are sequences of rational numbers whose sequence members pile up in the manner described, but without having a limit value in the set of rational numbers. An example of this is the sequence of rational numbers with the formation rule (see Heron method )

${\displaystyle a_{1}:=1,\quad a_{i+1}:={\frac {a_{i}}{2}}+{\frac {1}{a_{i}}}}$.

This sequence is a Cauchy sequence, but it has the irrational number as its limit and therefore does not converge within the set of rational numbers. The problem that many limit values ​​of Cauchy sequences are not contained in the set of rational numbers led to the idea of completing the number range to the set of real numbers. ${\displaystyle {\sqrt {2}}}$ ${\displaystyle \mathbb {Q} }$ ${\displaystyle \mathbb {R} }$

Cauchy sequences in metric spaces

definition

More generally, the term Cauchy sequence is defined for metric spaces , i.e. arbitrary sets on which a metric is given. A sequence of elements in is called a Cauchy sequence if ${\displaystyle (X,d)}$ ${\displaystyle X}$ ${\displaystyle d}$ ${\displaystyle (x_{i})_{i\in \mathbb {N} }}$ ${\displaystyle X}$

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad d(x_{m},x_{n})<\varepsilon }$

applies. So there is an index for every real number , so that for all natural numbers the distance between the corresponding members of the sequence is. ${\displaystyle \varepsilon >0}$ ${\displaystyle N}$ ${\displaystyle m,n\geq N}$ ${\displaystyle d(x_{m},x_{n})<\varepsilon }$

A geometric formulation equivalent to this is: For each there is a point and an index , so that all terms ab in the open sphere lie around the point with a radius . This version only differs from the convergence definition in that here the center point may depend on the radius , while in the case of convergence the limit value of must be independent. ${\displaystyle \varepsilon >0}$ ${\displaystyle a}$ ${\displaystyle N}$ ${\displaystyle x_{N}}$ ${\displaystyle B_{\varepsilon }(a)}$ ${\displaystyle a}$ ${\displaystyle \varepsilon }$ ${\displaystyle a}$ ${\displaystyle \varepsilon }$ ${\displaystyle a}$ ${\displaystyle \varepsilon }$

completeness

Every convergent sequence in a metric space is also a Cauchy sequence. If a sequence converges to a limit value , then there is an index for each , so that applies to all . With the triangle inequality for metric spaces it then follows for all ${\displaystyle (x_{i})_{i\in \mathbb {N} }}$ ${\displaystyle x\in X}$ ${\displaystyle \varepsilon >0}$ ${\displaystyle N\in \mathbb {N} }$ ${\displaystyle d(x,x_{n})<{\tfrac {\varepsilon }{2}}}$ ${\displaystyle n\geq N}$ ${\displaystyle m,n\geq N}$

${\displaystyle d(x_{m},x_{n})\leq d(x_{m},x)+d(x,x_{n})<{\tfrac {\varepsilon }{2}}+{\tfrac {\varepsilon }{2}}=\varepsilon }$

and the sequence is thus a Cauchy sequence. However, the reverse direction does not necessarily have to be true, which ultimately led to the introduction of complete rooms . In a complete space, by definition, every Cauchy sequence has a limit value and the concept of the convergent sequence coincides with the concept of the Cauchy sequence. However, each incomplete metric space, by the formation of equivalence classes of Cauchy sequences completed be. Two Cauchy sequences and of elements in are considered equivalent if ${\displaystyle (x_{i})_{i\in \mathbb {N} }}$ ${\displaystyle (y_{i})_{i\in \mathbb {N} }}$ ${\displaystyle X}$

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad d(x_{m},y_{n})<\varepsilon }$

or what is the same

${\displaystyle \lim _{m,n\in \mathbb {N} }d(x_{m},y_{n})=0}$.

If the limit value is in one of the two sequences , then also that of the other, and the two limit values ​​are the same. ${\displaystyle X}$

See also

• Cauchy criterion
• Cauchy network

Web links

Wikibooks: Math for Non-Freaks: Cauchy Sequences and the Cauchy Criterion  - Learning and Teaching Materials

literature

• Konrad Königsberger : Analysis 1 . Springer, Berlin 2004, ISBN 3-540-41282-4
• Konrad Königsberger : Analysis 2. Springer-Verlag, Berlin / Heidelberg, 2000, ISBN 3-540-43580-8
• Otto Forster : Analysis 1. Differential and integral calculus of a variable. Vieweg-Verlag, 8th edition 2006, ISBN 3-528-67224-2

References and comments

1. ↑ order to guide a rebuttal, it is necessary to reverse the definition: . ${\displaystyle \exists \varepsilon >0~\forall N\in \mathbb {N} ~\exists m,n\geq N\colon \left|a_{m}-a_{n}\right|\geq \varepsilon }$
2. ↑ Dirk Werner : Functional Analysis . 2005, p. 2 .