Zindler curve

Zindler curve: Each of the chords of the same length halves the length of the curve and its area.

Examples of Zindler curves: convex (red) and non-convex

A Zindler curve is a closed, colon-free curve in the plane with the property that

(L) all the tendons that bisect the curve are the same length.

The simplest example of a Zindler curve is a circle . But Konrad Zindler discovered in 1921 that there were other such curves and described a construction method. In 1938, Herman Auerbach was the first to use the name Zindlerkurven (courbes de Zindler) .

An equivalent characteristic of the Zindler curves is that

(F) all chords that bisect the inner surface of the closed curve are of equal length. These are the same tendons that also halve the length of the curve.

Examples:
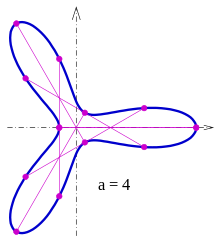
Each of the curves dependent on the family parameter (described in the complex plane for simplicity) ${\displaystyle a}$

${\displaystyle z(u)=x(u)+iy(u)=e^{2iu}+2e^{-iu}+ae^{iu/2}\;,\ u\in [0,4\pi ]\;,}$

is for a Zindler curve. For the curve is even convex. The curves for (blue), (green) and (red) can be seen in the drawing . From the curve can be derived from a constant thickness . ${\displaystyle a>4}$
${\displaystyle a\geq 24}$
${\displaystyle a=8}$ ${\displaystyle a=16}$ ${\displaystyle a=24}$
${\displaystyle a\geq 8}$

The curve with a = 4 is NOT a Zindler curve because there are chords that have a third point in common with the curve.

Proof of property (L) : From the derivation

${\displaystyle z'(u)=i{\Big (}2e^{2iu}-2e^{-iu}+{\frac {a}{2}}e^{iu/2}{\Big )}\;}$ surrendered

${\displaystyle |z'(u)|^{2}=z'(u){\overline {z'(u)}}=\cdots =8+{\frac {a^{2}}{4}}-8\cos 3u\;.}$

Thus there is a - periodic function and the equation holds for each ${\displaystyle |z'(u)|}$ ${\displaystyle 2\pi }$ ${\displaystyle u_{0}}$

${\displaystyle \int _{u_{0}}^{u_{0}+2\pi }|z'(u)|\,du=\int _{0}^{2\pi }|z'(u)|\,du\;.}$

The latter is half the length of the curve. The tendons that bisect the curve length, so be prepared by curve points to describe. The length of such a chord results ${\displaystyle \;z(u_{0})\;,\;z(u_{0}+2\pi )\;}$ ${\displaystyle u_{0}\in [0,4\pi ]}$

${\displaystyle |z(u_{0}+2\pi )-z(u_{0})|=\cdots =|2ae^{iu_{0}/2}|=2a}$

and this is therefore independent of . ${\displaystyle u_{0}}$

There are some of the tendons described here that have a third point in common with the curve (see picture). So only the curves of the sample group with Zindler curves can be . (The proof that no other points have in common with the curve for the chords used was not given here.) ${\displaystyle a=4}$ ${\displaystyle a>4}$ ${\displaystyle a>4}$

literature

• Herman Auerbach: Sur unproblemème de M. Ulam concernant l'équilibre des corps flottants. (PDF; 796 kB), Studia Mathematica 7, 1938, pp. 121–142.
• KL Mampel: About Zindler curves. Journal for pure and applied mathematics 234, 1969, pp. 12-44.
• Konrad Zindler: About convex structures. Part II. Monthly books for mathematics and physics 31, 1921, pp. 25–56.

Individual evidence

1. ↑ W. Wunderlich: Algebraic examples of plane and spatial Zindler curves. Publ. Math. Debrecen 24: 289-297 (1977) (p. 291).