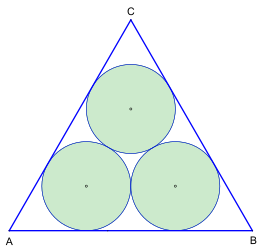
Malfatti circle

The three Malfatti circles of a triangle are circles , each of which touches at least two sides of the triangle and at least one of the other two circles.

Malfatti circles are named after Gianfrancesco Malfatti , who stated their construction in 1803 and assumed that they solved the Malfatti problem of packing three circles into a triangle that do not intersect and have maximum area .

The following picture shows Malfatti's solution to the problem of constructing three circles that touch each other and two sides of the triangle, as Malfatti's construction problem.

The following applies to the radii of the Malfatti circles of a triangle ABC:

${\displaystyle r_{A}={\frac {r}{2(s-a)}}(s-r-({\overline {IB}}+{\overline {IC}}-{\overline {IA}}))}$

${\displaystyle r_{B}={\frac {r}{2(s-b)}}(s-r-({\overline {IC}}+{\overline {IA}}-{\overline {IB}}))}$

${\displaystyle r_{C}={\frac {r}{2(s-c)}}(s-r-({\overline {IA}}+{\overline {IB}}-{\overline {IC}}))}$

It stands for the incircle radius and half the circumference of the triangle. is the center of the circle and and are the three bisectors . ${\displaystyle r}$ ${\displaystyle s}$ ${\displaystyle I}$ ${\displaystyle \omega _{\alpha },\omega _{\beta },}$ ${\displaystyle \omega _{\gamma }}$

History

The marble problem
Triangular prism with three inscribed cylindrical columns, as well as with the nine possible points of contact of the Malfatti circles.

The original Malfatti problem referred to a problem from stereotomy , the supposed solution of which Malfatti found in 1802 and published in 1803 in the Memoria di Matematica e Fisica della Società Italiana delle Scienze in his article Memoria sopra un problema stereotomico . At the beginning of his article, Malfatti formulates the task at hand.

Freely translated it reads:

In the case of a right triangular prism made of any material, for example marble, three [circular] cylinders are cut from it with the same height as the prism, but with the highest possible total volume, i.e. with the least possible material waste of the prism volume.

In his article Memoria sopra un problema stereotomico , Malfatti also points out that this stereotomic task can be reduced to a problem of surface geometry. He defines the position of the circles inscribed in the triangle, now called Malfatti circles, as follows:

Free translation

Given a triangle, construct three circles in it so that each of the circles is tangent (that is, they touch a point) with the other two and with two sides of the triangle.

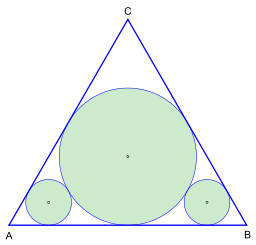
However, this was refuted in 1994 by Zalgaller and Los, who showed that the solution is instead achieved by inscribing a circle with the largest area in successive steps; Shown below in the area of ​​the triangle being covered by three circles .

As early as 1687, the Malfatti construction problem was solved by Jakob I Bernoulli in a special case (isosceles triangle) and later Jakob Steiner (1826, Crelle's Journal) gave purely geometrical solutions and Alfred Clebsch , the latter with elliptical functions (1857, Crelle's Journal). The Japanese Ajima Naonobu also came up with a solution 30 years before Malfatti in the context of Japanese architecture. That the Malfatti construction did not solve the Malfatti problem in all cases was shown by Lob and Richmond in 1930, and it was later shown that it only does this in the rarest of cases.

Geometric constructions

Ingmar Lehmann explains various solutions to the Malfatti problem in his analysis in 2003. The Malfatti problem - a topic in the promotion of gifted students . Three methods are described in detail below.

Malfatti construction

Malfatti circles according to Malfatti

Variant with previous calculations

"An elementary geometric construction that dispenses with previous algebraic calculations is relatively demanding." 

For this purpose, Lehmann derives three equations with the help of the Pythagorean theorem and the similarity of triangles , the solutions of which are provided by the tangent segments and . ${\displaystyle x\;={\overline {AC_{1}}},\;y={\overline {BC_{2}}}}$ ${\displaystyle z={\overline {CA_{2}}}}$

The following relationships are also taken into account:

${\displaystyle {\overline {AI}}={\sqrt {r^{2}+s^{2}}},\;\;\;{\overline {BI}}={\sqrt {r^{2}+t^{2}}},\;\;\;{\overline {CI}}={\sqrt {r^{2}+u^{2}}},}$

therein the terms mean

${\displaystyle s={\overline {AL_{c}}},\;t={\overline {BL_{c}}}}$ and ${\displaystyle u={\overline {CL_{a}}}.}$

With the appropriate values ​​used, it is now possible to determine a so-called auxiliary route ${\displaystyle {\overline {PQ}}}$ with the length ${\displaystyle m}$

${\displaystyle m={\frac {1}{2}}\left({\overline {AI}}+{\overline {BI}}+{\overline {CI}}-{\overline {AL_{c}}}-{\overline {BL_{c}}}-{\overline {CL_{a}}}+r\right),}$

then applies to the length ${\displaystyle m}$

${\displaystyle x={\overline {AI}}-m,\;\;\;y={\overline {BI}}-m\;\;\;z={\overline {CI}}-m.}$

If the factor is shifted to the expression in brackets, ${\displaystyle {\frac {1}{2}}}$

${\displaystyle m=\left({\frac {1}{2}}{\overline {AI}}+{\frac {1}{2}}{\overline {BI}}+{\frac {1}{2}}{\overline {CI}}-{\frac {1}{2}}{\overline {AL_{c}}}-{\frac {1}{2}}{\overline {BL_{c}}}-{\frac {1}{2}}{\overline {CL_{a}}}+{\frac {1}{2}}r\right),}$

a very simple and space-saving geometrical construction (see adjacent picture) can be displayed.

Construction description

After drawing a z. B. unequal-sided triangle with the side lengths and the center of the inscribed circle is determined using the three bisectors and . This results in the lines and The following is the dropping of the perpendicular from onto the line with the base point and the drawing of the inscribed circle around with the radius The falling of the perpendicular from up to the base point and from up to the base point follows. ${\displaystyle ABC}$ ${\displaystyle a,\;b}$ ${\displaystyle c}$ ${\displaystyle I}$ ${\displaystyle \omega _{\alpha },\omega _{\beta },}$ ${\displaystyle \omega _{\gamma }}$ ${\displaystyle {\overline {AI}},{\overline {BI}}}$ ${\displaystyle {\overline {CI}}.}$ ${\displaystyle I}$ ${\displaystyle {\overline {BC}}}$ ${\displaystyle L_{a}}$ ${\displaystyle k}$ ${\displaystyle I}$ ${\displaystyle {\overline {IL_{a}}}.}$ ${\displaystyle I}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle L_{b}}$ ${\displaystyle I}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle L_{c}}$

Now the length of the auxiliary route is determined on a straight line as follows . First, the track halves and added, from the sum of the track halves and is subtracted from the obtained residue, and finally the half Inkreisradius added. ${\displaystyle m}$ ${\displaystyle {\overline {PQ}}}$ ${\displaystyle {\frac {1}{2}}{\overline {AI}},\;{\frac {1}{2}}{\overline {BI}}}$ ${\displaystyle {\frac {1}{2}}{\overline {CI}}}$ ${\displaystyle {\frac {1}{2}}{\overline {AL_{c}}},\;{\frac {1}{2}}{\overline {BL_{c}}}}$ ${\displaystyle {\frac {1}{2}}{\overline {CL_{a}}}}$ ${\displaystyle {\frac {1}{2}}r}$

It continues with the determination of the centers of the Malfatti circles. In other words, tap the auxiliary section with the compass and transfer it to the three bisectors and from the center of the inscribed circle ; this results in the points and from the points and an arc up to the side of the triangle and from an arc up to and including the points and It follows the erection of three perpendiculars from the base points and on the relevant bisector and thus the sought center points and result ${\displaystyle {\overline {PQ}},}$ ${\displaystyle m,}$ ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ ${\displaystyle \omega _{\gamma }}$ ${\displaystyle I}$ ${\displaystyle D,\;E}$ ${\displaystyle F.}$ ${\displaystyle D}$ ${\displaystyle E}$ ${\displaystyle c}$ ${\displaystyle F}$ ${\displaystyle a}$ ${\displaystyle C_{1},\;C_{2}}$ ${\displaystyle A_{2}.}$ ${\displaystyle C_{1},\;C_{2}}$ ${\displaystyle A_{2}}$ ${\displaystyle \omega _{\alpha },\omega _{\beta },}$ ${\displaystyle \omega _{\gamma };}$ ${\displaystyle M_{A},\;M_{B}}$ ${\displaystyle M_{C}.}$

To get the points of contact and , three plumb bobs have to be felled from the center points and onto the triangle sides and again . Finally, draw in the Malfatti circles and with the radii and and you get their last three points of contact and ${\displaystyle B_{2},\;A_{1}}$ ${\displaystyle B_{1}}$ ${\displaystyle M_{A},\;M_{B}}$ ${\displaystyle M_{C}}$ ${\displaystyle b,\;a}$ ${\displaystyle b}$ ${\displaystyle k_{A},\;k_{B}}$ ${\displaystyle k_{C}}$ ${\displaystyle r_{A},\;r_{B}}$ ${\displaystyle r_{C}}$ ${\displaystyle G,\;H}$ ${\displaystyle J.}$

Thus the three Malfatti circles and with their nine possible points of contact and are constructed. ${\displaystyle k_{A},\;k_{B}}$ ${\displaystyle k_{C}}$ ${\displaystyle C_{1},\;C_{2},\;A_{1},\;A_{2},\;B_{1},\;B_{2},\;G,\;H}$ ${\displaystyle J}$

Construction according to Steiner-Petersen

Jakob Steiner generalized the Malfatti problem in 1826 by introducing three incircles made up of three partial triangles as a construction element. Steiner formulated the following sentence:

"Each of the common tangents of the Malfatti circles touches two of the three incircles of the partial triangles at the same time, with the center of the incircle of the triangle being." ${\displaystyle \triangle BCI,\;\triangle CAI,\triangle ABI,}$ ${\displaystyle I}$ ${\displaystyle \triangle ABC}$ 

Petersen found an elementary geometric solution in 1879, which is shown below.

The Malfatti circles generated using the Steiner-Petersen method have the same radii as the Malfatti circles constructed using the Malfatti method.

Construction description

For the sake of clarity, it is advantageous to show the construction in three main steps, (1) - (3). Only the relevant construction elements are transferred from the first to the second or from the second to the third main step.

Malfatti circles according to Steiner-Petersen
(1) Main step: Construction of the three incircles of the partial triangles and ${\displaystyle \triangle BCI,\;\triangle CAI}$ ${\displaystyle \triangle ABI.}$

(1) Construction of the three incircles of the partial triangles and ${\displaystyle \triangle BCI,\;\triangle CAI}$ ${\displaystyle \triangle ABI.}$

After drawing a z. B. unequal-sided triangle with the side lengths and the center of the inscribed circle is determined using the three bisectors and . The Inkreismittelpunkte and the sub-triangles and again obtained as the intersection of two bisectors, z. B. by quartering the angles and It follows the falling of the perpendicular to the line with the base point and the drawing of the inscribed circle around with the radius Felling the perpendicular from up to the base point and from up to the base point and the drawing of the last two Incircles and around their midpoints or are connected. ${\displaystyle ABC}$ ${\displaystyle a,\;b}$ ${\displaystyle c,}$ ${\displaystyle I}$ ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ ${\displaystyle \omega _{\gamma }}$ ${\displaystyle M_{P},\;M_{Q}}$ ${\displaystyle M_{R}}$ ${\displaystyle \triangle BCI,\;\triangle CAI}$ ${\displaystyle \triangle ABI}$ ${\displaystyle \alpha ,\;\beta ,}$ ${\displaystyle \gamma .}$ ${\displaystyle M_{P}}$ ${\displaystyle {\overline {BC}}}$ ${\displaystyle P}$ ${\displaystyle k_{P}}$ ${\displaystyle M_{P}}$ ${\displaystyle {\overline {M_{P}P}}.}$ ${\displaystyle M_{Q}}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle Q}$ ${\displaystyle M_{R}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle R}$ ${\displaystyle k_{Q}}$ ${\displaystyle k_{R},}$ ${\displaystyle M_{Q}}$ ${\displaystyle M_{R},}$

Malfatti circles according to Steiner-Petersen
(2) main step: construction of the three tangents and ${\displaystyle {\overline {RZ}},{\overline {PX}}}$ ${\displaystyle {\overline {QY}}}$

(2) Construction of the three tangents and ${\displaystyle {\overline {RZ}},{\overline {PX}}}$ ${\displaystyle {\overline {QY}}}$

It continues with the connecting points with the bisecting the track in and drawing in the Thales circle He cuts the inscribed circle in the points and now attracts you the first tangent from the point through the point where the inscribed circle until they reach the side of the triangle in cuts. ${\displaystyle R}$ ${\displaystyle M_{P},}$ ${\displaystyle {\overline {RM_{P}}}}$ ${\displaystyle M_{1}}$ ${\displaystyle k_{1}.}$ ${\displaystyle k_{P}}$ ${\displaystyle K}$ ${\displaystyle L.}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle k_{P},}$ ${\displaystyle b}$ ${\displaystyle Z}$

Then connect with and cut the route in half and draw the Thaleskreis . He cuts the inscribed circle in the points and the plotting of the second tangent from the point through until they reach the side of the triangle in cuts, deliver the intersection Since a point on the third tangent must be, it requires for its determination only a line of by up to the side of the triangle and the point of intersection . The third tangent is thus determined. ${\displaystyle P}$ ${\displaystyle M_{Q}}$ ${\displaystyle {\overline {PM_{Q}}}}$ ${\displaystyle M_{2}}$ ${\displaystyle k_{2}}$ ${\displaystyle k_{Q}}$ ${\displaystyle O}$ ${\displaystyle N.}$ ${\displaystyle P}$ ${\displaystyle N}$ ${\displaystyle b}$ ${\displaystyle X}$ ${\displaystyle T.}$ ${\displaystyle T}$ ${\displaystyle Q}$ ${\displaystyle T}$ ${\displaystyle c}$ ${\displaystyle Y.}$ ${\displaystyle {\overline {QY}}}$

Malfatti circles according to Steiner-Petersen
[3] Main step: Construction of the Malfatti circles and ${\displaystyle k_{A},k_{B}}$ ${\displaystyle k_{C}}$

(3) Construction of the Malfatti circles and ${\displaystyle k_{A},\;k_{B}}$ ${\displaystyle k_{C}}$

First, the bisector from the point to the bisector is drawn in the triangle ; this results in the center of the first Malfatti circle. This is followed by dropping the perpendicular from onto the line with the base point and drawing the first Malfatti circle around with the radius. Felling the perpendicular from up to with the base point and from the tangent to the base point follows. The following line down through to the bisector creates the center point. After the second Malfatti circle has been drawn in with the radius , the perpendiculars are cut from up with the base point from up with the base point and from on the tangent with the base point . The following line down through to the bisector creates the center point. Now the third Malfatti circle is drawn in around with the radius ${\displaystyle ARZ}$ ${\displaystyle \omega _{\epsilon }}$ ${\displaystyle R}$ ${\displaystyle \omega _{\alpha }}$ ${\displaystyle M_{A}}$ ${\displaystyle M_{A}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle C_{1}}$ ${\displaystyle k_{A}}$ ${\displaystyle M_{A}}$ ${\displaystyle {\overline {M_{A}C_{1}}}.}$ ${\displaystyle M_{A}}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle B_{2}}$ ${\displaystyle M_{A}}$ ${\displaystyle RZ}$ ${\displaystyle C'}$ ${\displaystyle M_{A}}$ ${\displaystyle C'}$ ${\displaystyle \omega _{\beta }}$ ${\displaystyle M_{B}.}$ ${\displaystyle k_{B}}$ ${\displaystyle M_{B}}$ ${\displaystyle {\overline {M_{B}C'}}}$ ${\displaystyle M_{B}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle C_{2},}$ ${\displaystyle M_{B}}$ ${\displaystyle {\overline {BC}}}$ ${\displaystyle A_{1}}$ ${\displaystyle M_{B}}$ ${\displaystyle PX}$ ${\displaystyle A'}$ ${\displaystyle M_{B}}$ ${\displaystyle A'}$ ${\displaystyle \omega _{\gamma }}$ ${\displaystyle M_{C}.}$ ${\displaystyle k_{C}}$ ${\displaystyle M_{C}}$ ${\displaystyle {\overline {M_{C}A'}}.}$

To the points of contact and to obtain, it still requires two solders precipitated from the center on of on and the connection of the point with ${\displaystyle A_{2},\;B_{1}}$ ${\displaystyle B'}$ ${\displaystyle M_{C}}$ ${\displaystyle {\overline {BC}},}$ ${\displaystyle M_{C}}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle M_{A}}$ ${\displaystyle M_{C}.}$

Thus the three Malfatti circles and with their nine possible points of contact and are constructed. ${\displaystyle k_{A},\;k_{B}}$ ${\displaystyle k_{C}}$ ${\displaystyle C_{1},\;C_{2},\;A_{1},\;A_{2},\;B_{1},\;B_{2},\;A',\;B'}$ ${\displaystyle C'}$

Construction according to Lob and Richmond

Construction according to H. Lob and HW Richmond,
equilateral triangle with inscribed circle, as a circle from the three Malfatti circles

H. Lob and HW Richmond published a solution in 1930, in which the inscribed circle of the equilateral exit triangle is used as a circle of three. The coverage of the triangular area by this arrangement of the circles is only marginally greater, namely by , but the task is easy and can be represented with little effort. ${\displaystyle \approx 1\,\%}$

You have proven

"[...] that the so-called Malfatti circles, i.e. those three circles that each have exactly two of the triangle sides as tangents, do not provide the maximum coverage of a triangle." 

Construction description

After drawing an equilateral triangle with sides of equal length and , the center of the inscribed circle is determined using the three bisectors and . Then the plumb bob is dropped on the line with the base point and the inscribed circle around with the radius the intersection points are with the bisector and with the bisector.The plumb bob from up to the base point and from up to the base point follows . ${\displaystyle ABC}$ ${\displaystyle a,\;b}$ ${\displaystyle c}$ ${\displaystyle I}$ ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ ${\displaystyle \omega _{\gamma }}$ ${\displaystyle I}$ ${\displaystyle {\overline {BC}}}$ ${\displaystyle D}$ ${\displaystyle k}$ ${\displaystyle I}$ ${\displaystyle {\overline {ID}};}$ ${\displaystyle E}$ ${\displaystyle \omega _{\alpha }}$ ${\displaystyle F}$ ${\displaystyle \omega _{\beta }.}$ ${\displaystyle I}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle G}$ ${\displaystyle I}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle H}$

For the smaller circles one draws two parallels to the line segment (in an equilateral triangle) One from the point to the line with the intersection , the second from the point to the line with the intersection The establishment of the perpendicular with the base point on the bisector and Establishing the perpendicular bisector with the base point results in the center points and now a circle is drawn around with the radius and a circle around with the radius . In order to get the last two points of contact, two plumb bobs are then felled on, from and from , resulting in the base points and ${\displaystyle {\overline {AB}}.}$ ${\displaystyle E}$ ${\displaystyle {\overline {AC}}}$ ${\displaystyle J}$ ${\displaystyle F}$ ${\displaystyle {\overline {BC}}}$ ${\displaystyle K.}$ ${\displaystyle J}$ ${\displaystyle \omega _{\alpha }}$ ${\displaystyle \omega _{\beta }}$ ${\displaystyle K}$ ${\displaystyle M_{A}}$ ${\displaystyle M_{B}.}$ ${\displaystyle M_{A}}$ ${\displaystyle {\overline {M_{A}E}}}$ ${\displaystyle M_{B}}$ ${\displaystyle {\overline {M_{B}F}}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle M_{A}}$ ${\displaystyle M_{B}}$ ${\displaystyle L}$ ${\displaystyle M.}$

Thus the three circles and with their nine possible points of contact and are constructed in the equilateral triangle . ${\displaystyle k,\;k_{A}}$ ${\displaystyle k_{B}}$ ${\displaystyle D,\;E,\;F,\;G,\;H,\;J,\;K,\;L}$ ${\displaystyle M}$

The triangle is covered by three circles

"The correct solution always uses the inscribed circle of the starting triangle as one of the three circles, maW, one of the circles always touches all three sides of the triangle." 

• The Malfatti method as well as the Steiner-Petersen method achieved

${\displaystyle \left({\sqrt {3}}-{\frac {1}{2}}\right)\cdot \pi \approx 0{,}72910}$ or approx. ${\displaystyle 72{,}91\,\%.}$

• The Lob and Richmond method achieved

${\displaystyle \left({\frac {11{\sqrt {3}}}{81}}\right)\cdot \pi \approx 0{,}73895}$ or approx. ${\displaystyle 73{,}90\,\%.}$

• Method with inscribed circle according to Zalgaller and Los.

The coverage of the triangular area, e.g. B. as a percentage value, depends on the selected shape of the starting triangle. The shape shown is achieved with for the corresponding areas ${\displaystyle A}$

${\displaystyle {\frac {A_{k_{1}}+A_{k_{2}}+A_{k_{3}}}{A{_{\triangle {ABC}}}}}\cdot 100\,\%\approx 72{,}70\;\%}$

• 

  Method according Malfatti and the method according to Steiner-Petersen in an equilateral triangle, covering the triangular area about 72.91%

• 

  Method according to Lob and Richmond in the equilateral triangle, coverage of the triangular area approx. 73.90%

• 

  Method according to Zalgaller and Los, coverage of the triangular area depends on the selected shape of the starting triangle; in the form shown the coverage of the triangular area is approx. 72.70%

literature

• Kurt Loeber: Contributions to the solution and history of the Malfatti problem and its extensions. Inaugural dissertation. SUB Göttingen, Göttingen Digitization Center, 1914, accessed on October 7, 2018 . 
• Marco Andreatta, Andras Bezdek, Jan P. Boronski The Malfatti Problem: two centuries of debate , Mathematical Intelligencer, 2011, No. 1
• Heinrich Dörrie : Malfatti's Problem in 100 Great Problems of Elementary Mathematics: Their History and Solutions . Dover, New York 1965, ISBN 0-486-61348-8 , pp. 147-151.
• M. Goldberg: On the Original Malfatti Problem . In Math. Mag. No. 40, 1967, pp. 241-247.
• Charles Stanley Ogilvy: Excursions in Geometry . Dover, New York 1990, ISBN 0-486-26530-7 .
• VA Zalgaller, GA Los: The solution of Malfatti's problem . In: Journal of Mathematical Sciences . 72, No. 4, 1994, pp. 3163-3177.

Web links

• Eric W. Weisstein : Malfatti Circles . In: MathWorld (English).
• Eric W. Weisstein : Malfatti's Problem . In: MathWorld (English).
• Malfatti's problem cut-the-knot.org

Individual evidence

1. ^ Andreatta et al. a. Mathematical Intelligencer, 2011, No. 1, see References
2. ↑ ^{a b c} Raúl Ibáñez: El problema de Malfatti. culturacientifica, Matemoción, April 5, 2017, accessed October 5, 2018 (Spanish). 
3. ↑ ^{a b} Kurt Loeber: Historical overview (introduction). In: Contributions to the solution and history of the Malfattian problem and its extensions. SUB Göttingen, Götinger Digitization Center, 1914, p. 2 ff , accessed on October 7, 2018 . 
4. ↑ Praise, Richmond On the Solution of Malfatti's Problem for a Triangle , Proc. London Math. Soc. 2, 287-304, 1930
5. ^ Goldberg On the Original Malfatti Problem , Mathematics Magazine, Volume 40, 1967, pp. 241-247
6. ↑ ^{a b} Ingmar LEHMANN: Construction of the Malfatti circles, pp. 3–5. (PDF) In: The Malfatti Problem - A Topic in Promoting Talented Students, 15 pages. TU Dortmund University, 2003, accessed on October 2, 2018 . 
7. ↑ Ingmar LEHMANN: Construction according to Steiner-Petersen, page 5. (PDF) In: The Malfatti problem - a topic in the promotion of the gifted. TU Dortmund University, 2003, accessed on October 2, 2018 . 
8. ↑ Ingmar LEHMANN: Construction according to Steiner-Petersen, p. 8 ff. (PDF) In: The Malfatti problem - a topic in the promotion of gifted students. TU Dortmund University, 2003, accessed on October 2, 2018 . 
9. ↑ Ingmar LEHMANN: Construction according to Lob and Richmond, p. 2. (PDF) In: The Malfatti Problem - A Topic in Promoting the Gifted. TU Dortmund University, 2003, accessed on October 2, 2018 .