Jones formalism

The Jones formalism describes linear optical images taking polarization into account . It was named after R. Clark Jones who introduced this representation in 1941. The light is represented as a plane electromagnetic wave with a complex two - dimensional Jones vector , the amplitude of the wave, and can therefore be used to describe optical effects such as interference . The formalism thus represents an improvement compared to the Stokes parameters . In contrast, however, the Jones formalism is limited to fully polarized, coherent light. The maps are represented by Jones matrices . With them, the Jones formalism enables the modeling and analysis of optical systems in which a light beam passes through a cascade of optical components.

Mathematical description

Examples of normalized Jones vectors

polarization	Direction of polarization at different times at z = 0	Jones vector	Bra-ket notation
linear in x-direction		${\displaystyle {\begin{pmatrix}1\\0\end{pmatrix}}}$	${\displaystyle |H\rangle }$
linear in y-direction		${\displaystyle {\begin{pmatrix}0\\1\end{pmatrix}}}$	${\displaystyle |V\rangle }$
linear in + 45 ° direction		${\displaystyle {\frac {1}{\sqrt {2}}}{\begin{pmatrix}1\\1\end{pmatrix}}}$	${\displaystyle |D\rangle ={\frac {1}{\sqrt {2}}}(|H\rangle +|V\rangle )}$
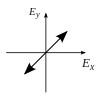
left circular		${\displaystyle {\frac {1}{\sqrt {2}}}{\begin{pmatrix}1\\\mathrm {i} \end{pmatrix}}}$	${\displaystyle |L\rangle ={\frac {1}{\sqrt {2}}}(|H\rangle +\mathrm {i} |V\rangle )}$
right circular		${\displaystyle {\frac {1}{\sqrt {2}}}{\begin{pmatrix}1\\-\mathrm {i} \end{pmatrix}}}$	${\displaystyle |R\rangle ={\frac {1}{\sqrt {2}}}(|H\rangle -\mathrm {i} |V\rangle )}$

In complex notation, the elongation of a monochromatic plane wave in a Cartesian coordinate system is location and time dependent

${\displaystyle {\vec {E}}(z,t)={\begin{pmatrix}{\tilde {E}}_{x}\\{\tilde {E}}_{y}\end{pmatrix}}e^{\mathrm {i} (kz-\omega t)}}$,

where the -axis is selected as the direction of propagation . The real numbers and denote the circular wave number or the circular frequency of the wave. The complex numbers or describe the phase and amplitude of the or component of the field. The Jones vector of this wave is then ${\displaystyle z}$ ${\displaystyle k}$ ${\displaystyle \omega }$ ${\displaystyle {\tilde {E}}_{x}}$ ${\displaystyle {\tilde {E}}_{y}}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle {\vec {J}}={\begin{pmatrix}{\tilde {E}}_{x}\\{\tilde {E}}_{y}\end{pmatrix}}}$,

that is, the explicit space and time dependency of the amplitude is suppressed when describing the wave. Furthermore, in the representation of a Jones vector, its components are usually normalized to 1 and a prefactor introduced so that the intensity remains unchanged (see examples).

The effect of an optical component on the light wave can be described by the effect of a complex-valued 2 × 2 matrix on the Jones vector if the element has no non-linear properties, ${\displaystyle \mathbf {M} }$

${\displaystyle {\vec {J}}_{\rm {out}}={\mathbf {M} }{\vec {J}}_{\rm {in}}.}$

If the light beam passes through a system of optical elements with Jones matrices , the overall effect of the optical system can be determined by a Jones matrix ${\displaystyle \mathbf {M} _{1},\ldots ,\mathbf {M} _{n}}$

${\displaystyle {\mathbf {M} }={\mathbf {M} }_{n}\cdot {\mathbf {M} }_{n-1}\cdot \ldots \cdot {\mathbf {M} }_{1}}$

describe (provided that multiple reflections between the individual components are irrelevant). The eigenpolarizations of an optical system correspond to the eigenvectors of its Jones matrix. The Jones vector is only suitable for describing completely polarized light, and accordingly only optical components that do not have any depolarizing properties can be characterized by Jones matrices. If depolarization effects are important, the more complex Stokes formalism must be used.

Jones matrices can e.g. B. describe linear polarizations or circular polarizations (rotation of the plane of polarization) and retardation plates. In the quarter plate z. B. delayed a polarization direction compared to the perpendicular to it by a quarter wavelength. With circular polarization and delay, the amount of the total amplitude does not change, and the matrices are unitary , the following applies (where complex means conjugate and T the transposition of the matrix) and . In the case of linear polarization, the amount of the total amplitude can change; the associated matrices are not unitary. ${\displaystyle \lambda }$ ${\displaystyle M^{-1}=M^{\dagger }:={\overline {M}}^{\rm {T}}}$ ${\displaystyle {\overline {M}}}$ ${\displaystyle {|M\cdot {\vec {J}}|}^{2}=({\vec {J}}^{*T}\cdot M^{\dagger }M\cdot {\vec {J}})=({\vec {J}}^{*T}\cdot {\vec {J}})={|{\vec {J}}|}^{2}=J^{2}}$

Examples of Jones matrices

Optical element	Jones matrix
Polarization filter for linearly polarized light in H position	${\displaystyle {\begin{pmatrix}1&0\\0&0\end{pmatrix}}}$
Polarization filter for linearly polarized light, in V position	${\displaystyle {\begin{pmatrix}0&0\\0&1\end{pmatrix}}}$
Polarization filter for linearly polarized light, in + 45 ° position	${\displaystyle {\frac {1}{2}}{\begin{pmatrix}1&1\\1&1\end{pmatrix}}}$
Polarization filter for linearly polarized light, in the −45 ° position	${\displaystyle {\frac {1}{2}}{\begin{pmatrix}1&-1\\-1&1\end{pmatrix}}}$
Polarization filter for linearly polarized light, rotated by the angle in the mathematically positive direction of rotation from the H position ${\displaystyle \varphi }$	${\displaystyle {\begin{pmatrix}\cos ^{2}\varphi &\cos \varphi \sin \varphi \\\sin \varphi \cos \varphi &\sin ^{2}\varphi \end{pmatrix}}}$
Polarizer for left circularly polarized light	${\displaystyle {\frac {1}{2}}{\begin{pmatrix}1&-\mathrm {i} \\\mathrm {i} &1\end{pmatrix}}}$
Polarizer for right circularly polarized light	${\displaystyle {\frac {1}{2}}{\begin{pmatrix}1&\mathrm {i} \\-\mathrm {i} &1\end{pmatrix}}}$
λ / 2 plate with fast axis in x-direction	${\displaystyle {\begin{pmatrix}-\mathrm {i} &0\\0&\mathrm {i} \end{pmatrix}}=e^{-\mathrm {i} {\frac {\pi }{2}}}\;{\begin{pmatrix}1&0\\0&e^{\mathrm {i} \pi }\end{pmatrix}}=-\mathrm {i} \;{\begin{pmatrix}1&0\\0&-1\end{pmatrix}}}$
λ / 4 plate with fast axis in x-direction	${\displaystyle {\frac {1}{\sqrt {2}}}{\begin{pmatrix}1-\mathrm {i} &0\\0&1+\mathrm {i} \end{pmatrix}}=e^{-\mathrm {i} {\frac {\pi }{4}}}\;{\begin{pmatrix}1&0\\0&e^{\mathrm {i} {\frac {\pi }{2}}}\end{pmatrix}}=e^{-\mathrm {i} {\frac {\pi }{4}}}\;{\begin{pmatrix}1&0\\0&\mathrm {i} \end{pmatrix}}}$

According to the usual way of speaking in optics, "H" as horizontal and "V" as vertical denote the orientation in the x and y directions. If the interference with other rays is not important, a common (complex) phase prefactor can be factored out, and the matrices are often specified in such a way that the first diagonal position is real.

Turned components

If an optical component is rotated by the angle θ with respect to its optical axis , then the Jones matrix for the rotated component is M ( θ ). This matrix is ​​obtained from the matrix M for the non-rotated component by the following transformation:

${\displaystyle M(\theta )=R(\theta )\,M\,R(-\theta ),}$

It is ${\displaystyle R(\theta )={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}.}$

Transition to quantum mechanics

The pure x and pure y polarization can be understood as an orthonormal basis and represented in Bra-Ket notation, as indicated in the table above. A polarization filter can then be understood, for example, as a quantum mechanical operator that projects onto an eigenstate of the system (pure x or y polarization) ( collapse of the wave function ). The corresponding projector would be for an x-polarization filter: The eigenvalue then corresponds to the portion of the incident light that has the corresponding polarization. The observable is the polarization in the x direction. The filters specified above for circularly polarized light can be constructed analogously. ${\displaystyle |H\rangle \langle H|}$

A base change can also be easily carried out in the Bra-Ket representation . The base change matrix , which is converted from the x / y base into the representation by superposition of oppositely circularly polarized waves, has the following form. ${\displaystyle S}$

${\displaystyle S={\begin{pmatrix}\langle H|R\rangle &\langle H|L\rangle \\\langle V|R\rangle &\langle V|L\rangle \end{pmatrix}}}$

Such considerations offer a clear reference to the otherwise rather abstract formalisms of quantum mechanics.

literature

• R. Clark Jones: New Calculus for the Treatment of Optical Systems. I. Description and discussion of the calculus . In: Journal of the Optical Society of America . tape 31 , no. 7 , 1941, pp. 488-493 , doi : 10.1364 / JOSA.31.000488 .
• RMA Azzam, NM Bashara: Ellipsometry and Polarized Light. North-Holland, Amsterdam ( inter alia) 1987, ISBN 0-7204-0694-3 .
• A. Gerrard, J. Burch: Introduction to Matrix Methods in Optics. John Wiley, 1975 ( limited preview in Google Book search).
• Frank Pedrotti, Leno Pedrotti: Introduction to Optics. 2nd edition, Prentice Hall, 1993, ISBN 0-13-501545-6 (Chapter 14: Matrix Treatment of Polarization).

Web links

• Jones Matrix at Science World

Individual evidence

1. ^ Frank L. Pedrotti, Leno S. Pedrotti: Introduction to Optics . Prentice-Hall, 1993, ISBN 0-13-016973-0 , pp. 288 .
2. ^ Eugene Hecht: Optics . 4th edition. Addison-Wesley Longman, Amsterdam 2001, ISBN 0-8053-8566-5 , pp. 375 .
3. ↑ ^{a b} With the representation of the right and left circular polarization one has to note that a factor has been chosen for the propagation of the plane wave , whereby among other things the formulas for left and right circular polarization are interchanged. Both conventions (opposite sign in the exponent) are used in the specialist literature, which must be taken into account when using formulas from the fields of optics and physics. ${\displaystyle e^{\mathrm {i} (kz-\omega t)}}$
4. ^ Gordon Baym: Lectures on Quantum Mechanics . 3. Edition. Westview Press, New York 1990, ISBN 0-8053-0667-6 , pp. 1-37 .