Bremsstrahlung
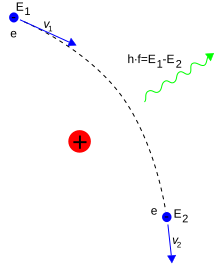
Brake radiation is the electromagnetic radiation generated by the acceleration of an electrically charged particle, e.g. B. of an electron . Contrary to the name given, this radiation occurs not only when the amount of speed decreases, but also when it increases or the speed only changes its direction. Brake radiation in the narrower sense is when particles are slowed down in matter .
From the point of view of quantum electrodynamics , the generation of bremsstrahlung can be explained by the fact that every interaction of charged particles is connected with the emission or absorption of photons , the quanta of electromagnetic radiation.
Occurrence or application
In particle accelerators (especially synchrotrons ) and storage rings, braking radiation is released when charged particles are deflected by a magnetic field , which in this context is called synchrotron radiation .
The bremsstrahlung effect is used in X-ray tubes to generate X-rays . This involves shooting electrons with a kinetic energy of 30 k eV or more onto a metal plate, which is often made of tungsten . A small part of the energy released during braking is converted into X-rays with a continuous spectrum (an X-ray continuum ).
Brake radiation can also influence the development and morphology of electrical discharges and generate high-energy terrestrial gamma-ray bursts and positrons .
Physics of bremsstrahlung
The electromagnetic field of moving charges is described by the Liénard-Wiechert potentials . Then the electric field and the magnetic field are through
given. Designate it
- the unit vector between the observation point and the position of the particle,
- the distance between the observation point and the location of the particle
- the electrical charge of the particle,
- the speed in units of the speed of light,
- the Lorentz factor ,
- the speed of light,
- the electric field constant and
- the subscript that the arguments are to be evaluated at the retarded time .
In this form, the electric and magnetic fields are divided into a speed field, which only depends on the current speed, and an acceleration field. The acceleration field has a dependency proportional to , so that its power density does not disappear in infinity. It is therefore a radiation field.
The component of the Poynting vector of this radiation field in the direction of observation, which corresponds to the power density, is
according to the radiated power at the retarded time per solid angle element
- .
This is the relativistic generalization of the Larmor formula for the energy loss of accelerated charges.
The frequency spectrum of the bremsstrahlung results from a Fourier transformation of the total energy emitted
With
- the intensity ,
- the angular frequency and
- the trajectory of the charged particle .
Spectral distribution of the bremsstrahlung of an X-ray tube

Towards short wavelengths , the spectrum has a cut-off wavelength that corresponds to the kinetic energy of the electrons, i.e. H. the entire kinetic energy of the electrons is converted into X-rays. This cut-off wavelength depends only on the acceleration voltage passed through ( anode voltage ); it is independent of the anode material; the shape of the spectrum depends on the speed distribution of the electrons and the metal used.
The shortest possible wavelength (see Duane-Hunt law ) occurs when the entire kinetic energy of the electron is converted into the radiant energy of a single photon :
With
- the elementary charge of the electron
- the acceleration or anode voltage of the X-ray tube
- the Planck's constant
- the frequency .
With
- ( c for the speed of light )
follows
Inserting the natural constants h, c and e results in the tailored size equation :
The lower limit wavelength depends only on the acceleration voltage ; at an acceleration voltage of 25 kV it is 0.05 nm . This radiation can already penetrate normal glass and thin aluminum plates. For this reason, radiation protection measures must be taken in the case of color picture tubes that work with acceleration voltages of 25 to 27 kV (black and white picture tube: approx. 18 kV) . Lead glass is therefore used for the flask.
According to Kramers, the continuous energy distribution of the bremsstrahlung when electrons enter a material is linear over the frequency. After conversion to the wavelength representation, the result is:
With
- the Kramers constant ,
- the electron flow and
- the atomic number of the atoms of the material .
In relation to the spectral number density of the photons results
With real spectra of X-ray emissions, the braking radiation that arises is superimposed by various effects. In addition, there is especially the characteristic radiation (peaks in the figure), which represents an emission spectrum of the atoms of the material, as well as its absorption bands , since the bremsstrahlung occurs under the material surface.
Electron-electron bremsstrahlung
An important process for small atomic numbers is the scattering of free electrons on the shell electrons of an atom or molecule. Since this electron-electron bremsstrahlung is a function of , but the electron-nuclear bremsstrahlung is a function of , the electron-electron bremsstrahlung can be neglected for metals . For air, however, it plays an important role in generating terrestrial gamma-ray bursts .
Web links
- desy.de: X-ray light - bremsstrahlung
- X-ray brake radiation spectrum
Individual evidence
- ↑ Köhn, C., Chanrion, O., Neubert, T. The influence of bremsstrahlung on electric discharge streamers in N 2 , O 2 gas mixtures Plasma Sources Sci. Technol. (2017), vol. 26, 015006. doi : 10.1088 / 0963-0252 / 26/1/015006 .
- ↑ Köhn, C., Ebert, U. Calculation of beams of positrons, neutrons, and protons associated with terrestrial gamma ray flashes Journal Geophys. Res. (2015), vol. 120, pp. 1620-1635. doi : 10.1002 / 2014JD022229 .
- ↑ John David Jackson: Classical Electrodynamics . 3. Edition. De Gruyter, Berlin • New York 2002, ISBN 3-11-016502-3 , pp. 766 .
- ↑ John David Jackson: Classical Electrodynamics . 3. Edition. De Gruyter, Berlin • New York 2002, ISBN 3-11-016502-3 , pp. 771-772 .
- ↑ John David Jackson: Classical Electrodynamics . 3. Edition. De Gruyter, Berlin • New York 2002, ISBN 3-11-016502-3 , pp. 779 .
- ↑ Ulm University: X-ray brake radiation
- ↑ XCIII. On the theory of X-ray absorption and of the continuous X-ray spectrum HA Kramers in Philos. Mag. Ser. 6, 46 (1923) Pages 836-871 doi : 10.1080 / 14786442308565244
- ↑ Frédéric Tessier, Iwan Kawrakow: Calculation of the electron – electron bremsstrahlung cross-section in the field of atomic electrons . In: Nuclear Instruments and Methods in Physics Research Section B . tape 266 , no. 4 , 2008, p. 625-634 , doi : 10.1016 / j.nimb.2007.11.063 .
- ↑ Köhn, C., Ebert, U. The importance of electron-electron Bremsstrahlung for terrestrial gamma-ray flashes, electron beams and electron-positron beams J. Phys. D .: Appl. Phys. as Fast Track Communication (2014), vol. 47, 252001. ( abstract )


![{\ displaystyle {\ begin {aligned} {\ vec {E}} ({\ vec {x}}, t) & = {\ frac {q} {4 \ pi \ varepsilon _ {0}}} \ left [ {\ frac {{\ vec {n}} - {\ vec {\ beta}}} {\ gamma ^ {2} (1 - {\ vec {\ beta}} \ cdot {\ vec {n}}) ^ {3} R ^ {2}}} \ right] _ {\ text {ret}} + {\ frac {q} {4 \ pi \ varepsilon _ {0} c}} \ left [{\ frac {{\ vec {n}} \ times [({\ vec {n}} - {\ vec {\ beta}}) \ times {\ dot {\ vec {\ beta}}}]} {(1 - {\ vec { \ beta}} \ cdot {\ vec {n}}) ^ {3} R}} \ right] _ {\ text {ret}} \\ {\ vec {B}} ({\ vec {x}}, t) & = {\ frac {1} {c}} \ left [{\ vec {n}} \ times {\ vec {E}} \ right] _ {\ text {ret}} \ end {aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/df219e8698af895381965ca04616b432a4f5c2c4)












![{\ displaystyle \ left [{\ vec {n}} \ cdot {\ vec {S}} \ right] _ {\ text {ret}} = {\ frac {q ^ {2}} {16 \ pi ^ { 2} \ varepsilon _ {0} c}} \ left [{\ frac {1} {R ^ {2}}} \ left | {\ frac {{\ vec {n}} \ times [({\ vec { n}} - {\ vec {\ beta}}) \ times {\ dot {\ vec {\ beta}}}]} {(1 - {\ vec {\ beta}} \ cdot {\ vec {n}} ) ^ {3}}} \ right | ^ {2} \ right] _ {\ text {ret}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a46f90f3b4274b938c2674d5b0a575a7d8f6897)


![{\ displaystyle {\ frac {\ mathrm {d} P (t ')} {\ mathrm {d} \ Omega}} = {\ frac {q ^ {2}} {16 \ pi ^ {2} \ varepsilon _ {0} c}} {\ frac {\ left | {\ vec {n}} \ times [({\ vec {n}} - {\ vec {\ beta}}) \ times {\ dot {\ vec { \ beta}}}] \ right | ^ {2}} {(1 - {\ vec {n}} \ cdot {\ vec {\ beta}}) ^ {5}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/311c1e147c0af1ea599b6a05637ef5c47187e36f)
![{\ displaystyle {\ frac {\ mathrm {d} ^ {2} I} {\ mathrm {d} \ omega \, \ mathrm {d} \ Omega}} = {\ frac {q ^ {2}} {16 \ pi ^ {3} \ varepsilon _ {0} c}} \ left | \ int _ {- \ infty} ^ {\ infty} \ mathrm {d} t \, {\ frac {{\ vec {n}} \ times [({\ vec {n}} - {\ vec {\ beta}}) \ times {\ dot {\ vec {\ beta}}}]} {(1 - {\ vec {\ beta}} \ cdot {\ vec {n}}) ^ {2}}} e ^ {\ mathrm {i} \ omega (t - {\ vec {n}} \ cdot {\ vec {x}} (t) / c) } \ right | ^ {2} = {\ frac {q ^ {2}} {16 \ pi ^ {3} \ varepsilon _ {0} c}} \ omega ^ {2} \ left | \ int _ {- \ infty} ^ {\ infty} \ mathrm {d} t \, {\ vec {n}} \ times ({\ vec {n}} \ times {\ vec {\ beta}}) e ^ {\ mathrm { i} \ omega (t - {\ vec {n}} \ cdot {\ vec {x}} (t) / c)} \ right | ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f137d7d8318c0473a3776ff87a29aa4649bd89)



















