Electrochemical double layer
Electrochemical double layer , electrolytic double layer or double layer for short are common names for boundary layers at which electrically separated charged layers face each other.
construction
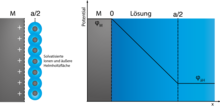
As a rule, the electrochemical double layer is understood to be the phase boundary between an electron conductor (the electrode ) and an ion conductor (the electrolyte ). A “double layer” also occurs at the liquid-liquid phase boundary of immiscible electrolytes. Typically, two charge layers face each other at the phase boundary in the charged state, which - as in every capacitor - have opposite signs. The discharged double layer carries the so-called zero charge potential on the electrodes , at which the metal side is uncharged and the solution side also carries no net charge. The "thickness" of the charged layers, i.e. H. the mean dimension perpendicular to the surface is about 0.1 nm in metals and 0.1 to 10 nm in solution; it is described by the Debye length . In the solution it depends on the mobility of the ions and the concentration of the solution, in the metal it is mainly dependent on the electron density, since the atomic cores in fixed electrodes are immobile.
Historical development of ideas about the double layer
Helmholtz model
Hermann von Helmholtz made the first considerations and investigations into double layers, see also the article Helmholtz layer .
Gouy-Chapman model
The early Helmholtz model only described a constant differential capacitance independent of the charge density and only dependent on the dielectric constant and the thickness of the double layer. But this model is only a good basis for describing charge separation. It does not take into account important factors such as diffusion or mixing of ions in the solvent, the possibility of ions being adsorbed on the surface of the electrode and the interaction between dipole moments in the solvent and in the electrode.
That is why the theory of Helmholtz was further developed by Louis Georges Gouy in 1910 and by David Leonard Chapman in 1913 . They assumed a thermal movement of the counterions in the electrolyte, which led to the formation of a diffuse layer extending over several molecular layers, the so-called Gouy-Chapman double layer , which is voltage-dependent and also depends on the concentration of the ions. In this model, the charge distribution of ions in the electrolyte is understood as a function of the distance from the metal surface and can be described with the Boltzmann statistics . This means that the electrical potential decreases exponentially from the surface of the liquid.
Star model
However, the Gouy-Chapman model fails with a heavily charged double layer. In 1924 Otto Stern combined the ideas of Helmholtz with those of Gouy and Chapman. In his model of the double layer, the layer in the electrolyte is composed of a rigid and an adjoining diffuse layer, so that the model of the star double layer results. This model takes into account the fact that ions are finite in size. Consequently, the closest possible approach of the ions to the electrode is of the order of magnitude of the ion radius.
Grahame
But Stern's model still has some limitations, for example the ions are only modeled as point charges, with the only significant interaction in the diffuse layer being that of an electrical charge , and the permittivity across the double layer is assumed to be constant, as is the viscosity of the electrolyte .

That is why David C. Grahame modified the Stern model in 1947, taking into account the solvent and solvation as well as the specific adsorption. In the Grahame model, the Helmholtz layer is bounded towards the solid phase by the inner Helmholtz surface ( English inner Helmholtz plane , IHP). It runs through the centers of adsorbed molecules of the solvent. To the liquid phase out it is through the outer Helmholtz surface ( English plane outer Helmholtz , OHP) limited and extends through the center points of the solvated ions in their distance of closest approach to the electrode. As in the star model, the diffuse layer lies outside the OHP. The ions are solvated by molecules of the solvent. This results in a structure of three layers: a solvent layer (also: inner Helmholtz layer), a layer of solvated counterions (also: outer Helmholtz layer) and a diffuse layer. In addition, Grahame described for the first time the effect of ions that have stripped off their enveloping solvation layer and touched the surface of the electrodes, although the electrode surface should actually be completely covered with solvated molecules of the electrolyte solvent. He called the accumulation of these ions on the metallic surface of an electrode “specific adsorption”.
Bockris-Müller-Devanathan model
In 1963, the electrochemist John O'Mara Bockris, together with Klaus Müller and Michael Angelo Vincent Devanathan, formulated their model of the different storage principles in electrical double layers, which, in addition to the ideas of the previous models, also takes into account the influence of the solvent on the overall effect of the double layer. With this " BMD model ", named in the order of the author names in the publication , the redox reaction, the basis of the pseudocapacity , was also described in more detail with the description of specifically adsorbed anions .
The BMD model is clearly shown in the picture. On the charged electrode, the solvent molecules adsorbed on the electrode surface form the inner Helmholtz layer. The solvated cations in the outer Helmholtz layer, which attach directly to the inner Helmholtz layer, are the counterions to the ions in the electrode and form the double-layer capacitance. In between, a specifically adsorbed cation has penetrated the inner Helmholtz layer, given its charge to the electrode with a redox reaction (pseudocapacitance) and has thus become an anion .
Schmickler and Henderson
As has been shown experimentally, the capacities of the inner double layer also clearly depend on the electrode metal used. The models mentioned so far all describe the distribution of the charges in the electrolyte and the resulting double-layer capacitance without going into the properties of the electrode material. Therefore, they cannot explain differences caused by different metals. A first double-layer model that tried to reproduce the contribution of the metal was presented as early as 1928. As Schmickler and Henderson have shown, the contribution of some metals to the double-layer capacitance can be estimated using the relatively simple Jellium model, which describes the interaction of the electron gas with the lattice of the metal ions.
Trasatti-Buzzanca
Further research on double layers with electrodes made of ruthenium dioxide led in 1971 by Sergio Trasatti and Giovanni Buzzanca to the realization that the electrochemical charging behavior of specifically adsorbed ions at low voltages is similar to that of capacitors. The specifically adsorbed ions provided a charge transfer between the ion and the electrode and later provided what is known as "pseudocapacitance". It was the first step towards pseudocapacitors .
Conway
Between 1975 and 1980 Brian Evans Conway carried out basic research on redox processes on electrodes doped with ruthenium oxide . He described 1991 the transition of the behavior of a capacitor to a (rechargeable) battery ( From Supercapacitor to Battery ) in the electrochemical energy storage and 1999, he coined the term "super capacitor" ( English Supercapacitor to identify those capacitors Faraday with the charge storage by) Redox reactions on the electrode surfaces have a significantly higher pseudocapacitance compared to the static double-layer capacitance.
The type of capacitor for which Conway coined the term supercapacitor stored the electrical charge mainly in the form of pseudocapacitance, a term that Conway used as early as 1962. Electrodes that were provided with metal oxides or conductive polymers provided particularly high values of pseudocapacitance. However, Conway was able to determine that the pseudocapacity was not based solely on “specifically adsorbed ions”. Further research results essentially provided three sources for the pseudocapacity: redox reactions, intercalation and electrosorption. The latter is an underpotential deposition of Ad atoms.
Marcus theory
The physical and mathematical basics of electron charge transfer without chemical bonds, which is the basis of pseudocapacity, were described by Rudolph Arthur Marcus . The Marcus theory named after him describes redox reactions (one-electron exchange reactions), in which the solvent is decisive during the reaction and allows the calculation of the Gibbs free activation enthalpy from the polarization properties of the solvent, the size and the distance between the reactants during electron transfer and the free enthalpy of the redox reaction. Marcus received the Nobel Prize in Chemistry in 1992 for this theory .
Applications
The existence of an electrochemical double layer that surrounds biological macromolecules ( proteins , nucleic acids ) in low-molecular electrolytes (buffer solutions) is an essential prerequisite for all methods of electrophoresis , which have become of crucial importance for the biochemistry of the macromolecules (see SDS gel electrophoresis , DNA sequencing ). The same applies to the often disruptive phenomenon of electroosmosis, which is less important in practice . In electrical engineering, the phenomenon of the double layer in supercapacitors , also known as "double-layer capacitors", as the sum of the double-layer capacitance and the pseudocapacitance, plays an important role.
See also
- Electrochemistry , for which the double layer is central
- Debye-Hückel theory , which is analogous to the models described and also uses the size called Debye length today
literature
- Héctor D. Abruña , Yasuyuki Kiya, Jay C. Henderson: Batteries and electrochemical capacitors . In: Physics Today . No. 12 , 2008, p. 43-47 ( PDF ).
- J. O'M. Bockris, MAV Devanathan, K. Muller: On the Structure of Charged Interfaces . In: Proceedings of the Royal Society . tape 274 , no. 1356 , 1963, pp. 55-79 , doi : 10.1098 / rspa.1963.0114 .
- BE Conway: Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications . Springer, Berlin 1999, ISBN 0-306-45736-9 ( limited preview in the Google book search).
- Volkmar M. Schmidt: Electrochemical process engineering. Basics, reaction technology, process optimization . Wiley-VCH, Weinheim 2003, ISBN 3-527-29958-0 , pp. 539–639 ( limited preview in Google Book Search - Chapter 7: Electrochemical Energy Technology ).
- Jiujun Zhang, Lei Zhang, Hansan Liu, Andy Sun, Ru-Shi Liu: Electrochemical Technologies for Energy Storage and Conversion . tape 1 . Wiley-VCH, Weinheim 2011, ISBN 978-3-527-32869-7 , pp. 317–376 ( limited preview in Google Book Search - Chapter 8: Electrochemical Supercapacitors ).
Individual evidence
- ↑ a b S. Srinivasan: Electrode / Electrolyte Interfaces: Structure and Kinetics of Charge Transfer . In: Fuel Cells . Springer, 2006, ISBN 978-0-387-25116-5 , pp. 27-92 .
- ↑ a b Adam Marcus Namisnyk and JG Zhu: A Survey of Electrochemical super-capacitor technology . 2003 ( PDF [accessed December 7, 2015] Bachelor thesis; University of Technology, Sydney; 2003).
- ↑ Gerald Ehrenstein: Surface charge (PDF; 79 kB) 2001. Archived from the original on September 28, 2011. Info: The archive link has been inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. Retrieved May 30, 2011.
- ↑ Otto Stern: On the theory of the electrolytic double layer . In: German Bunsen Society for Applied Physical Chemistry, Erich Müller (Hrsg.): Journal for Electrochemistry . tape 30 , no. 21-22 . Wiley ‐ VCH Verlag, November 1924, ISSN 0372-8323 , p. 508-516 , doi : 10.1002 / bbpc.192400182 ( online at the Electrochemical Science and Technology Information Resource (ESTIR) of the Electrochemical Society [PDF]).
- ↑ Gerald SMIRNOV: Electric Double Layer . 2011. Retrieved July 27, 2013.
- ^ David C. Grahame: The Electrical Double Layer and the Theory of Electrocapillarity. In: Chemical Reviews . tape 41 , no. 3 , December 1, 1947, p. 441-501 , doi : 10.1021 / cr60130a002 .
- ↑ Zbigniew Stojek: The Electrical Double Layer and Its Structure . In: Fritz Scholz (Ed.): Electroanalytical Methods: Guide to Experiments and Applications . Springer, Berlin / Heidelberg 2010, ISBN 978-3-642-02914-1 , p. 3-10 ( online ).
- ↑ M. Matsumoto: Electrocapillarity and double layer structure. In: H. Ohshima, K. Furusawa (Ed.) .: Electrical phenomena at interfaces: fundamentals, measurements, and applications. (= Surfactant science series. Vol. 76). 2nd ed. Marcel Dekker, New York 1998, pp. 87-99.
- ^ J. O'M Bockris, MAV Devanathan, K. Muller: On the Structure of Charged Interfaces . In: Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences . tape 274 , no. 1356 , June 25, 1963, pp. 55-79 , doi : 10.1098 / rspa.1963.0114 .
- ↑ Sergio Trasatti: Effect of the nature of the metal on the dielectric properties of polar liquids at the interface with electrodes. A phenomenological approach . In: Journal of Electroanalytical Chemistry and Interfacial Electrochemistry . tape 123 , no. 1 , 1981, p. 121-139 , doi : 10.1016 / S0022-0728 (81) 80047-2 .
- ^ Oscar Knefler Rice: Application of the Fermi Statistics to the Distribution of Electrons Under Fields in Metals and the Theory of Electrocapillarity . In: Physical Review . tape 31 , no. 6 , 1928, pp. 1051-1059 , doi : 10.1103 / PhysRev.31.1051 .
- ^ Wolfgang Schmickler , Douglas Henderson: The interphase between jellium and a hard sphere electrolyte. A model for the electric double layer . In: The Journal of Chemical Physics . tape 80 , no. 7 , 1984, pp. 3381-3386 , doi : 10.1063 / 1.447092 .
- ^ Wolfgang Schmickler, Douglas Henderson: New Models for the Structure of the Electrochemical Interface . In: Progress in Surface Science . tape 22 , no. 4 , 1986, pp. 323-419 , doi : 10.1016 / 0079-6816 (86) 90005-5 .
- ^ BE Conway: Transition from 'Supercapacitor' to 'Battery' Behavior in Electrochemical Energy Storage . In: Journal of The Electrochemical Society . tape 138 , no. 6 , May 1991, pp. 1539-1548 , doi : 10.1149 / 1.2085829 . ( PDF )
- ^ BE Conway: Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications . Springer, Berlin 1999, ISBN 0-306-45736-9 , pp. 1–8 ( limited preview in Google Book search). See also Brian E. Conway in Electrochemistry Encyclopedia: ELECTROCHEMICAL CAPACITORS Their Nature, Function, and Applications ( April 30, 2012 memento in the Internet Archive ) (accessed December 7, 2015)
- ^ AK Shukla, TP Kumar: PDF Pillars of Modern Electrochemistry: A Brief History . In: Electrochemistry Encyclopedia . November 2008, Central Electrochemical Research Institute.
- ^ BE Conway, E. Gileadi: Kinetic theory of pseudo-capacitance and electrode reactions at appreciable surface coverage . In: Transactions of the Faraday Society . tape 58 , no. 0 , 1962, p. 2493-2509 , doi : 10.1039 / TF9625802493 .
- ^ BE Conway, WG Pell: Double-layer and pseudocapacitance types of electrochemical capacitors and their applications to the development of hybrid devices . In: Journal of Solid State Electrochemistry . tape 7 , no. 9 , 2003, p. 637-644 , doi : 10.1007 / s10008-003-0395-7 .
- ↑ BE Conway, V. Birss, J. Wojtowicz: The role and utilization of pseudocapacitance for energy storage by supercapacitors . In: Journal of Power Sources . tape 66 , no. 1-2 , May 1997, pp. 1-14 , doi : 10.1016 / S0378-7753 (96) 02474-3 .