Fermat's principle

Analogy to Fermat's principle: What is the quickest way for a lifeguard to reach the drowning person?

The red path has the shortest running time t. The speed is on the beach and in the water . ${\displaystyle 4{\frac {m}{s}}}$ ${\displaystyle 1{\frac {m}{s}}}$

The Fermat principle (after Pierre de Fermat ) states that light in a medium takes paths between two points on which its transit time does not change with small variations of the path. In particular, the optical path length is extremal ; H. the longest or the shortest. It is also called the principle of the extremal optical path or the principle of the extremal transit time . The cause lies in the wave nature of the light and the associated interference . On non-extreme paths, the path length varies greatly with small variations in the path, and the interference is consequently destructive.

Snell's law of refraction and law of reflection can be derived from Fermat's principle . It also shows that light rays run straight in any homogeneous medium. This is also achieved by Huygens' principle , which is the local variant of Fermat's principle.

A related example

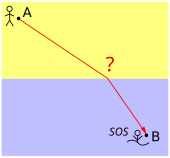
The derivation of the law of refraction from Fermat's principle is related to the question of which way a lifeguard should take if he wants to rescue someone from the water. The goal is of course to help the drowning person as quickly as possible. To do this, the lifeguard runs quickly on the beach to a point from which the path through the water is short, as he can only move slowly there. But if it runs too far, the portion of the path in the water is hardly any shorter, but the distance on land is significantly longer. In general, the fastest route is not the shortest (“beeline”).

The lifeguard doesn’t have to think twice, because if he just misses the optimal point, the time is hardly longer; at the optimal point, the time does not change at all with a small variation. This insensitivity to small variations is a special feature of the fastest route. It is the core of Fermat's principle.

Derivation of the law of refraction

Diagram for the derivation of Snell's law of refraction from Fermat's principle

The law of refraction of Snellius can be derived from Fermat's principle :

In the picture to the right of the beam sets off from top left through bottom right back. In the upper medium is the speed of light and in the lower part . This results in the running time t depending on the x-position of the point P: ${\displaystyle A=(0,a+b)}$ ${\displaystyle P=(x,b)}$ ${\displaystyle B=(d,0)}$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$

${\displaystyle t(x)=t_{1}+t_{2}={\frac {l_{1}}{c_{1}}}+{\frac {l_{2}}{c_{2}}}={\frac {\sqrt {x^{2}+a^{2}}}{c_{1}}}+{\frac {\sqrt {(d-x)^{2}+b^{2}}}{c_{2}}}}$

According to Fermat's principle, light takes the path with an extreme transit time. By deriving according to , we find the extreme values ​​of . ${\displaystyle x}$ ${\displaystyle t}$

${\displaystyle 0\;{\stackrel {!}{=}}\;{\frac {dt}{dx}}={\frac {1}{c_{1}}}{\frac {1}{2}}{\frac {1}{\sqrt {x^{2}+a^{2}}}}2x+{\frac {1}{c_{2}}}{\frac {1}{2}}{\frac {1}{\sqrt {(d-x)^{2}+b^{2}}}}2(d-x)(-1)}$

${\displaystyle \Leftrightarrow 0={\frac {1}{c_{1}}}{\frac {x}{\sqrt {x^{2}+a^{2}}}}-{\frac {1}{c_{2}}}{\frac {d-x}{\sqrt {(d-x)^{2}+b^{2}}}}}$

${\displaystyle \Leftrightarrow 0={\frac {1}{c_{1}}}{\frac {x}{l_{1}}}-{\frac {1}{c_{2}}}{\frac {d-x}{l_{2}}}}$

It is and . So it follows: ${\displaystyle \sin \alpha ={\frac {x}{l_{1}}}}$ ${\displaystyle \sin \beta ={\frac {d-x}{l_{2}}}}$

${\displaystyle \Leftrightarrow 0={\frac {1}{c_{1}}}\sin {\alpha }-{\frac {1}{c_{2}}}\sin {\beta }}$

${\displaystyle \Leftrightarrow {\frac {\sin {\alpha }}{\sin {\beta }}}={\frac {c_{1}}{c_{2}}}}$

There is still no proof that it is the minimum term.

Rays of light follow this law of refraction because it is the fastest way from to . ${\displaystyle A}$ ${\displaystyle B}$

The legitimate question arises as to how the light knows in advance which is the fastest way. Quantum mechanics provides the following answer:

It tries them all out at the same time.

In simplified terms, one can say that the contributions of all alternative paths are canceled out by incoherent overlapping.

Derivation of the law of reflection

Diagram for the derivation of the law of reflection from Fermat's principle

Just like the law of refraction, the law of reflection can also be derived with the help of Fermat's principle.

In the figure on the right, the light beam travels from left to right and is reflected in the mirror. Since the beam remains in a (homogeneous) medium, the same speed of light always applies . ${\displaystyle A=(0,a)}$ ${\displaystyle B=(d,b)}$ ${\displaystyle P=(x,0)}$ ${\displaystyle c}$

This results in the running time t depending on the x-position of the point P:

${\displaystyle t(x)=t_{1}+t_{2}={\frac {l_{1}}{c}}+{\frac {l_{2}}{c}}={\frac {\sqrt {x^{2}+a^{2}}}{c}}+{\frac {\sqrt {(d-x)^{2}+b^{2}}}{c}}}$

According to Fermat's principle, light takes the path with an extreme transit time. By deriving according to , we find the extreme values ​​of . ${\displaystyle x}$ ${\displaystyle t}$

${\displaystyle 0\;{\stackrel {!}{=}}\;{\frac {dt}{dx}}={\frac {1}{c}}{\frac {1}{2}}{\frac {1}{\sqrt {x^{2}+a^{2}}}}2x+{\frac {1}{c}}{\frac {1}{2}}{\frac {1}{\sqrt {(d-x)^{2}+b^{2}}}}2(d-x)(-1)}$

Multiplying both sides by gives you: ${\displaystyle c}$

${\displaystyle \Leftrightarrow 0={\frac {x}{\sqrt {x^{2}+a^{2}}}}-{\frac {d-x}{\sqrt {(d-x)^{2}+b^{2}}}}}$

${\displaystyle \Leftrightarrow 0={\frac {x}{l_{1}}}-{\frac {d-x}{l_{2}}}}$

It is and . So it follows: ${\displaystyle \sin \alpha ={\frac {x}{l_{1}}}}$ ${\displaystyle \sin \beta ={\frac {d-x}{l_{2}}}}$

${\displaystyle \Leftrightarrow \ 0=\sin {\alpha }-\sin {\beta }\Leftrightarrow \ \sin {\alpha }=\sin {\beta }}$

Because and are two angles in the interval and the sine is injective in this interval , the law of reflection follows: ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle [-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}]}$

${\displaystyle \alpha =\beta }$

There is still no proof that it is the minimum term.

Rays of light follow this law of reflection because it is the fastest way from to . ${\displaystyle A}$ ${\displaystyle B}$

The derivation of the law of reflection follows from that of the law of refraction, if one observes that the triangles "bottom right" (with and ) in the diagrams correspond. From with follows directly and . ${\displaystyle B}$ ${\displaystyle P}$ ${\displaystyle {\frac {\sin {\alpha }}{\sin {\beta }}}={\frac {c_{1}}{c_{2}}}}$ ${\displaystyle c_{1}=c_{2}}$ ${\displaystyle {\frac {\sin {\alpha }}{\sin {\beta }}}=1}$ ${\displaystyle \alpha =\beta }$

General mathematical formulation

The Cornu spiral illustrates the diffraction integral on which Fermat's principle is based.

Described mathematically, light passes through a medium, with the refractive index , of all possible paths between two points and precisely the path on which the transit time ${\displaystyle n(x)}$ ${\displaystyle X^{t}:t\mapsto x(t)=\left(ct,{\vec {x}}(t)\right)}$ ${\displaystyle x(t_{1})}$ ${\displaystyle x(t_{2})}$

${\displaystyle {\begin{aligned}t[X]&={\frac {1}{c}}\,\int _{t_{1}}^{t_{2}}n\left(X^{t}\right)\,{\sqrt {\left({\frac {\mathrm {d} X^{t}}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t\\&={\frac {1}{c}}\,\int _{t_{1}}^{t_{2}}n\left(x(t)\right)\,{\sqrt {c^{2}+\left({\frac {\mathrm {d} x(t)}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t\end{aligned}}}$

is stationary. The size is the time of flight between the two points. This corresponds to the Hamilton principle of the stationary action. ${\displaystyle t}$

Fermat's principle using the example of an ellipse

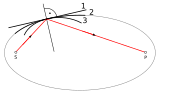
The transit time of light is usually a minimum, which means that every small change in the path increases the transit time. However, this does not always have to be the case, as the illustration on the right shows. Three possible cases are shown for a path between the two focal points and an ellipse . For any surface at the edge of this ellipse, the following applies: ${\displaystyle S}$ ${\displaystyle P}$

1. In the case of reflection on a surface with a smaller curvature than that of the ellipsoidal surface, the transit time is minimal.
2. In the case of reflection on the ellipsoidal surface, all points on the surface are equivalent: Moving the reflection point on the ellipsoidal surface does not change the transit time.
3. In the case of reflection on a surface with a greater curvature than that of the ellipsoidal surface, the running time is maximum compared with neighboring reflection points on this surface.

The Fermat principle in an inhomogeneous medium

In an inhomogeneous medium with a location-dependent refractive index, the light travels through curved paths. Therefore, the setting sun, for example, appears flattened: the rays of light from the upper edge of the sun are refracted less than those from the lower edge.

The phenomenon of the mirage also has its cause in an optically inhomogeneous medium. A layer of hot air forms over hot ground, such as a sunlit street, with a refractive index that is lower than that of the cooler air above. The rays of light that hit the hot air layer flatly are reflected back upwards.

In 1696, Johann I Bernoulli applied Fermat's principle to an optical medium with a variable refractive index in order to determine the shape of the brachistochrones , thus establishing the calculus of variations .

literature

• Florian Scheck: Theoretical Physics 3. Classical Field Theory . ISBN 3-540-42276-5 (Chapter 4.4 Geometric Optics, 4.4.3 Media with a negative refractive index).
• Roger Erb: Geometric optics with the Fermat principle In: Physics in school. 30, No. 9, 1992, pp. 291-295.

Web links

Wikibooks: Physics collection of exercises: The Fermat principle  - learning and teaching materials