major
Major (from Latin durus 'hard' ; French mode majeur , English major , Italian modo maggiore , Spanish modo mayor ) denotes a tone type in music . This can refer to a key , a scale or a chord .
In the course of the 18th century, major and minor replaced the terms modus major and modus minor ( cantus durus and cantus mollis ) for the pitches of the church modes . Since then, people have also spoken of the major-minor tonal system, or major-minor system for short .
- major minor
The major third between the fundamental and the third of the tone material under consideration is characteristic of the major character . The major third above the root is also major third called.
The auditory impression of major is often described as "bright, clear" (Latin durus = "hard"), whereas minor is often described as "dark, soft" (Latin mollis = "soft"). These characterizations should be used with caution. In particular, further associations such as B. Equating major with happy or minor with sad may apply, but should not be generalized under any circumstances, because the overall musical impression can depend on a large number of other components. So play u. a. Melodic-harmonic progressions and figures, tempo , instrumentation , dynamic parameters , but also text (if available), play a decisive role. So z. B. Mozart's Rondo alla Turca or Beethoven's piano piece Für Elise is hardly perceived as “sad”, although both compositions are in minor keys. In contrast, Herbert Grönemeyer's song Der Weg , even if the piece is in major, is regarded as a very sad composition.
For the spelling of key names, see the Notations section in the Keys article .
etymology
The expressions major and minor go back to the medieval doctrine of the hexachord . a. differentiated between the Hexachordum molle and the Hexachordum durum .
With the Hexachordum durum , starting from the note G , a higher variant of the note B , the B durum (our today's B ), was required as the third degree, while with the Hexachordum molle , starting from the tone F , one had to avoid this higher tone as the fourth degree ( Tritone ) and instead inserted the lower B minor .
To distinguish one listed in front of the lower tone B a small letter b with round abdomen ( b rotundum ) before the higher B a letter b with angular abdomen ( b quadratum ) later from which a H developed. The current form of the accidentals (a ♭ for the lower note, a ♯ for the higher note ) also goes back to this. The Italian names “bemolle” for the ♭ -sign and “bequadro” for the ♮ -symbol correspond to this .
The association of the tone genders with characteristics such as “hard” (= major) and “soft” (= minor) did not appear until much later with the disappearance of the church modes and the manifestation of the major-minor system, but has become firmly established in music theory and is still represented even in etymological dictionaries.
Major scale
Considered as a sequence of tones of whole and half steps, has the major scale (or major scale ) following structure: 1-1-½-1-1-1-½ (as two or tetrachords thought: 1-1-½ 1-1- ½). This corresponds to the ionic mode in its sequence of intervals . Since the 16th century it has been the most widely used scale in Western music, even before the minor scale. It is the most common scale for the occidental ear. The twelve major scales are each named after their starting tone. So z. B. the root tones C, D, E, F, G, A, B, c the C major scale.
The semitone steps between the third and fourth and the seventh and eighth tone are characteristic of the major scale . The remaining intervals are whole steps . The seventh tone has the function of a leading tone .
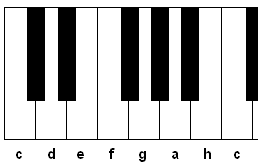
On a piano keyboard, the white keys, starting with C, make up a C major scale:
Audio sample:
Table showing all major scales
Each field in the table corresponds to a level of the chromatic scale . Keys with up to six (in exceptional cases seven) accidentals are common, i.e. 13 (or 15): the twelve scales shown in the table and - with enharmonic reinterpretation of D flat - C sharp major. Keys with more accidentals are theoretically possible, but not used for reasons of legibility.
The major scales are shown within an octave in such a way that the same tone levels correspond to the same colors. Repetitions of the scale steps outside the relevant octave are shown in black.

See also: Circle of Fifths
Relationships to minor
Minor parallel
For every major key there is a parallel key in minor , also called minor parallel, which contains the same tones (and is therefore notated with the same accidentals ) and begins a minor third lower (e.g. C major - A minor). This creates the sequence of whole and semitone steps that is typical for minor.
The major pentatonic scale also includes a parallel minor pentatonic scale, the root of which is a minor third lower. The blues is not so easily divided into major and minor, which is why blue scales have no parallels.
Minor variant
The variant key of a major key begins on the same keynote, but has different accidentals due to the different degrees in the minor. The minor variant is therefore always three steps down in the circle of fifths compared to the underlying major key. B. E major with four crosses , E minor but marked with a cross.
Table showing all minor scales
Each field in the table corresponds to a level of the chromatic scale .
The minor scales are shown within an octave in such a way that the same tone levels correspond to the same colors. Repetitions of the scale steps outside the relevant octave are shown in black.

See also: Circle of Fifths
Arrangement and relationship of the major and minor keys
| Sign : | 7 ♭ + fes
 |
6 ♭ + ces
 |
5 ♭ + total
 |
4 ♭ + des
 |
3 ♭ + as
 |
2 ♭ + es
 |
1 ♭ b
 |
0 ♭ / ♯ |
1 ♯ f sharp
 |
2 ♯ + c sharp
 |
3 ♯ + g sharp
 |
4 ♯ + dis
 |
5 ♯ + ais
 |
6 ♯ + ice
 |
7 ♯ + his
 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Major keys: | Ces | Ges | Of | As | It | B. | F. | C. | G | D. | A. | E. | H | F sharp | Cis |
| Minor keys: | as | it | b | f | c | G | d | a | e | H | f sharp | cis | g sharp | dis | ais |
See also: Circle of Fifths
Major triad
The components of the major triad (see also chord ) are the root, major third and fifth .
Acoustical basics of the major triad
That a major triad is perceived as harmonic can be explained by the fact that we are familiar with the overtone series as a natural sound phenomenon and that the major triad corresponds to the tones of the 4th to 6th order of this overtone series.
Very simplified example: When a low note A is played, a series of overtones also sound.
- Overtone series from A:
- A (110 Hz), A (220 Hz), E (330 Hz), A (440 Hz), C ♯ (550 Hz), E (660 Hz), G (770 Hz), A (880 Hz)
The 4th, 5th and 6th tone of this overtone series (A + C ♯ + E) together result in the triad A major in the pure tuning . The equally floating tuning common today can only approximate this ideal triad in terms of euphoria.
The 3rd, 4th and 5th tone (E + A + C ♯ ) and the 5th, 6th and 8th tone (C ♯ + E + A) each correspond to an inversion of the major triad.
The major triad, including its inversions, is therefore contained in the overtone series and thus a completely natural harmonic sound.
In the past, many works in minor (e.g. by Bach ) ended with a major chord (so-called Picardic third ), since only this was considered to be really conclusive. Only the major triad can produce the harmonic calm that is desired for a perfect final effect: A minor third would rub against the 5th tone of the overtone series above the fundamental and therefore be perceived as a clouding of the pure sound.
The step triads of C major
With the tone supply of the major scale, three major triads can be formed. These are on the first ( tonic ), fourth ( subdominant ) and fifth level ( dominant ).
In addition to these main level triads, triads can also be set up on the secondary levels. These are three minor triads and a diminished triad.

- Example of the C major scale
| Intervals → | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 1 | 2 | 3 | 4th | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sounds → | C. | D. | E. | F. | G | A. | H | C. | D. | E. | F. | Triad |
| Level ↓ | ||||||||||||
| 1 | C. | E. | G | C major | ||||||||
| 2 | D. | F. | A. | D minor | ||||||||
| 3 | E. | G | H | E minor | ||||||||
| 4th | F. | A. | C. | F major | ||||||||
| 5 | G | H | D. | G major | ||||||||
| 6th | A. | C. | E. | A minor | ||||||||
| 7th | H | D. | F. | h decreased |
If the semitone steps that lie between the tones are also taken into account in the table above, then it is relatively easy to deduce why only three major triads are possible with the seven tones of a major scale. (Each line in the following table can be thought of as a section of a piano keyboard with black keys. The triad notes are highlighted in black.) Each line begins with the root note of the corresponding triad.
| Semitones → | 0 | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intervals related to the root of the triad → |
1 | 2 ♭ | 2 | 3 ♭ | 3 | 4th | 4 ♯ 5 ♭ |
5 | 6 ♭ | 6th | 7 ♭ | j7 | Triad |
| Level sorted according to the circle of fifths ↓ |
|||||||||||||
| 4th | F. | G | A. | H | C. | D. | E. | F major | |||||
| 1 | C. | D. | E. | F. | G | A. | H | C major | |||||
| 5 | G | A. | H | C. | D. | E. | F. | G major | |||||
| 2 | D. | E. | F. | G | A. | H | C. | D minor | |||||
| 6th | A. | H | C. | D. | E. | F. | G | A minor | |||||
| 3 | E. | F. | G | A. | H | C. | C. | E minor | |||||
| 7th | H | C. | D. | E. | F. | G | A. | h decreased |
More major scales
The major scales in the broader sense (since they also contain a major third to the root) can also include the church modes Lydian and Mixolydian as well as the Phrygian-dominant scale , the Gypsy major and the harmonic major , which was introduced for systematic reasons .
Deviations
As defining as major and minor are for our listening habits, there are also musical concepts that deviate from the division into major and minor, e.g. B. Whole-tone scale , twelve-tone music or blues scales .
See also
Web links
Individual evidence
- ↑ See Wieland Ziegenrücker: ABC Music. General music theory. 6th, revised and expanded edition. Breitkopf & Härtel, Wiesbaden 2009, ISBN 978-3-7651-0309-4 , pp. 114–123.