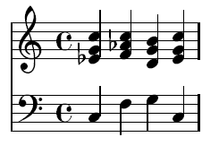Cadence (harmony)

from Wikipedia, the free encyclopedia

In today's music theory , cadenza ( Italian cadenza , from Latin cadere , to fall, to end ” ) usually refers to a chord progression that articulates the end of a section or a whole piece.

However, since the 18th century the term has been ambiguous. Since then it has also been used in harmony theory for certain chord progressions that are declared to be the basic building block of harmony and do not necessarily represent a conclusion. The music-theoretical writings of Jean-Philippe Rameau had a great influence here .

In the later 19th century Hugo Riemann also declared “cadence” to be the principle of musical form as a whole. Against this background, terms such as “extended cadence” and “ full cadence ” have become established.

In an even more general sense, the term is nowadays sometimes used for certain clichéd harmony sequences without these being elevated to a theoretical principle (e.g. Andalusian cadence ).

Cadence as the closing formula

In the late 15th century, the word cadence replaced the older term clausula ( clause ) in Italy as a term for final expressions . The chord progressions of many cadences in this sense are understandable from the combination of such clauses . Nowadays common subcategories of the term cadence as a closing formula, which are mainly used to describe music of the 18th and 19th centuries, include: a .:

The cadence (for example as a final formation and key confirmation) consists of the sequence tonic (I), subdominant (IV), dominant (V) and again tonic (I):

  • I - IV - V - I

Typical closing formulas in jazz include a. the sequence of stages:

Designations of final formulas from historical textbooks or from research literature on older repertoires are among others. a .:

Cadence as the basic building block of harmony

The transfer of the term cadence to chord progressions that do not serve as final turns goes back to Jean-Philippe Rameau . He pursued the idea that in the music of his time, chord connections before the end of a section are basically the same as those in the usual closing formulas. Therefore he tried to trace all chord connections (except chord changes after a final tonic ) to four types of " cadences ":

“Excepté le passage d'une tonique à quelque note que ce soit, tout est cadence, parfaite, rompue, interrompue ou irrégulière, en y comprenant leur imitation. »

"Apart from the transition from a tonic to whatever note, everything is cadence, perfect, broken, interrupted or irregular, including your imitations."

- Jean-Philippe Rameau : Code de musique pratique , Paris 1760, p. 140.

Here means:

  • cadence parfaite : fifth case in the fundamental bass after a dominant seventh chord
  • cadence rompue : Second rise in the fundamental bass after a dominant seventh chord
  • cadence interrompue : Third in the fundamental bass after a dominant seventh chord
  • cadence irrégulière : increase in fifths in the fundamental bass
\ new PianoStaff << \ new Staff {\ key c \ major \ time 1/1 \ override Staff.TimeSignature.transparent = ## t \ new Voice = "right" {\ relative c '' {\ clef treble <bdf g > 1 ^ \ markup {\ italic {parfaite}} <ce g> \ bar "||" <gbd f> 1 ^ \ markup {\ italic {rompue}} <gac e> \ bar "||" <fgb d> 1 ^ \ markup {\ italic {interrompue}} <e gis b d> \ bar "||" <c 'df a> 1 ^ \ markup {\ italic {irrégulière}} <ce g> \ bar "||" }}} \ new Staff {\ key c \ major \ time 1/1 \ override Staff.TimeSignature.transparent = ## t \ new Voice = "left" {\ relative c {\ clef "bass" g1 cgagefc}}} \ new FiguredBass {\ figuremode {<7> 1 r <7> <7> <7> <7 _ +> <6 5>}} >>

In terms of its harmony, a musical section is therefore a series of such “cadences” or chord progressions that are modeled on them (“ imitation ”). So z. B. a quintessential sequence from a chain of avoided or "simulated" cadences parfaites .

Cadence as a principle of "musical logic"

The connection of the main triads (chords of the 1st, 4th and 5th degree of a major or minor key, as tonic, subdominant and dominant) leads to the simple cadence, the basic cadence characterized by harmonic gradient, tension and relaxation. Even in his first publication explains Hugo Riemann the "so-called big cadenza" I-IV-IVI and tonic - subdominant -Tonika- dominant -Tonika for "type of all musical form." The term is charged here with a very high claim: In chord progressions like this one (or I-IV-VI) Riemann sees relationships that appear to him to be the principle of “musical logic” at all. The “logical meaning of harmonic turns” that the cadence shows should “form the basis of all sensible music creation” and “set a new barrier to arbitrariness” in times when compositional rules (such as the resolution of dissonances) are binding had lost and "freedoms of all kinds in harmonic sentences were allowed without hesitation".

The “logic” that Riemann recognizes in the cadence is inspired by the dialectic and the corresponding explanations by Johann Gottlieb Fichte and Moritz Hauptmann . In cadence I-IV-IVI the tonic appears differently. At first it is a mere assertion, "thesis", which is called into question by the subdominant, since the root of the I in the IV becomes the fifth. The subdominant is therefore "antithetical". The upper dominant then displaces this tone, but reclaims it with its third (the leading tone of the key). The upper dominant and final tonic are therefore "synthesis". The "main accords" I, IV and V could now be represented by the "secondary harmonies" II, III, VI and VII ("substitution"). By repeating chords, inserting secondary harmonies (e.g. I becomes I-VI), expanding the "thesis" (e.g. I becomes IVI) and repeating the "antithesis" and / or "synthesis" (e.g. I-II-VI-IV-IVI) would also result in “extended cadenzas”. Thus every successful “musical phrase” should be understood as an (extended) cadence.

Riemann later dropped the dialectical terminology and added the "four main stations of tonal cadence formation" and the like. a. described as: “Tonika (first statement). Subdominant (conflict). Upper dominant (solution of the conflict). Tonic (confirmation, conclusion). "

According to Riemann, the TDST sequence is problematic, “because after the upper dominant, the subdominant can only be understood through relation to the skipped tonic; the decline from the sub-dominant to the tonic is not a natural return of the part to the whole, and therefore does not have the perfect closing force of the sequence: the upper-dominant tonic. "

Full cadence

Since Riemann, the “complete cadence”, “simple cadence”, “main” or “full cadence” has been a starting point for numerous, especially German, harmony teachings:

Tonic Subdominant Dominant tonic (I IV VI) in all three positions.

As with Riemann, this chord connection serves as a “prototype and archetype” of tonal music or also as a “perfect image of tonality”. Since it includes all the tones of the scale, a key is clearly determined by it.

The word cadence has therefore strayed far from its original meaning as the final formula. So have about Michael Badger and Paul Söhner out that the Akkordverbindung I-IV-VI decays into two parts. In addition, according to Dachs / Söhner, the first tonic of the full cadence must be regarded as the “opening chord”, which does not belong to a final turn, but rather precedes one. The full cadence is therefore not a closing formula, but contains (at least) one. Therefore, Dachs / Söhner differentiate between “cadence” and (authentic, plagal, and half) “conclusions”.

Lars Ulrich Abraham defines “cadence” as “a group of chords from tonic to tonic” and sees in it “more than a harmonic final turn, namely a principle of order for all harmonics”. (He derives this strictly from the monody , i.e. the inherent final turns of individual voices.) This forces him to distinguish between "cadence" and "final cadence" or "final cadence" and "internal cadence", as well as to more precise cadence "as a final turn." ". His designation of the “full cadence” as “the most important cadenza for the Bach era” is misleading against this background. Either it can mean that sections in late baroque music usually end with the sequence TSDT, which is not the case without significant modifications to this chord sequence. Or it means quite generally that this music corresponds to the “archetype” of the TSDT sequence, as in the principles of Riemann's theory of function , which Abraham was not uncritically shared , unlike the music of Palestrina or Claude Debussy .

Practical advice on song accompaniment

Authentic cadenza in C major with the step sequence TDT
Plagale cadenza in C major with the steps TST
Full cadence in C major with the sequence TSDT
Authentic cadenza in C minor with tDt
Plagale cadenza in C minor with the steps tst
Full cadence in C minor with the steps tsDt

Many songs can only be accompanied by the sequences TDT, TST and / or TSDT, with the chords in their basic position. To accompany older songs that require a larger chord stock, to exercise recommended in basso .

TDT

Examples: Schubert: Sleep, sleep sweet, sweet boy , Oh dear Augustin , Beethoven: I love you, as you love me , The songs sound , No beautiful country , The cuckoo and the donkey , Weber: I'm not lonely , Today should be the big flax harvest etc.

TST

With this sequence begin z. B .: All the birds are already there , tomorrow Santa Claus is coming , Nobody Knows the Trouble I've Seen ( Spiritual ), Il était un 'bergère , God gracious the mighty Emperor frumme , Glory to the Father , The Sun Shines Bright .

TSDT

Many popular song melodies, which do not change the key: When I was a young journeyman , When the nightingales beat , So we part with song and sound , Whom God wants to show a real favor , A wild Aquarius is free , Come you shepherds , you little children Come on , O Strasbourg, O Strasbourg, you beautiful city , All the same a little funny , On the Saale bright beach , Gaudeamus igitur .

Function designations of the ladder's own triads

For three keys the area in the circle of fifths is highlighted (exemplary), which includes the main chords of the respective key:
C major (blue), E major (red), E flat major (yellow) or inside the circle of fifths: a -Moll (blue), C sharp minor (red), C minor (yellow).

In a major - or minor - scale can be at any stage (every sound) so-called diatonic triads create, each composed of said selected, the next but one and another two tones higher tone. A major scale therefore has the following scale-specific triads:

step Triad function Function symbol
I. major Tonic T
II minor Subdominant parallel Sp
III minor Dominant parallel or tonic counter-sound Dp or Tg
IV major Subdominant S.
V major Dominant D.
VI minor Tonic parallel or subdominant counter-sound Tp or Sg
VII reduced shortened dominant seventh chord Đ 7

In a (natural) minor scale it looks like this:

step Triad function Function symbol
I. minor Tonic t
II reduced
III major Tonic parallel or dominant counter- sound tP or dG
IV minor Subdominant s
V minor Minor dominant *) d
VI major Subdominant parallel or tonic counter-sound sP or tG
VII major Dominant parallel dP
*)In practice, instead of the ladder's own minor dominant, its major variant is usually used by raising the third in this triad (= leading tone to the tonic). In classical music, when a voice moves upwards, the 6th level (i.e. the level before the leading tone) is regularly increased in order to avoid an excessive second (melodic minor).

See also

Sources and literature

  • Lars Ulrich Abraham: Harmony. Vol. 1: The homophonic sentence (= Musik-Taschen-Bücher. 250 = Musik-Taschen-Bücher. Theoretica. 3). 3. Edition. Laaber-Verlag, Laaber 1984, ISBN 3-89007-001-9 (earlier editions in the music publisher Hans Gerig, Cologne 1965 and 1969).
  • Michael Dachs , Paul Söhner: Harmony Part 1. Kösel, Munich 1953, 11th edition 1985, ISBN 3-466-30013-4 .
  • Roland Eberlein , Jobst Fricke : Cadence perception and cadence history - a contribution to a grammar of music (= European University Writings Series 36: Musicology Vol. 79). Lang, Frankfurt am Main a. a. 1992, ISBN 3-631-44962-3 .
  • Roland Eberlein: The emergence of tonal sound syntax . Lang, Frankfurt am Main a. a. 1994, ISBN 3-631-47450-4 .
  • Roland Eberlein: The origin of the final cadenza in western music. In: Spektrum der Wissenschaft 7, 1995, pp. 62-71 ( online ).
  • August Halm : Harmony . Göschen, Berlin and Leipzig 1912.
  • Hanno Hussong: Studies on practical harmony teachings since 1945. dissertation.de, Berlin 2005, ISBN 3-89825-931-5 (At the same time: Saarbrücken, University, dissertation, 2004. Printed as a manuscript.).
  • Johannes Menke : The family of the cadenza doppia. In: Journal of the Society for Music Theory (ZGMTH). Vol. 8, No. 3, 2011, ISSN  1862-6742 , pp. 389-405, ( online) .
  • Diether de la Motte : Harmony (= dtv 30166). Joint original edition, 13th edition. Deutscher Taschenbuch-Verlag u. a., Munich a. a. 2004, ISBN 3-423-30166-X .
  • Alexander Rehding: Hugo Riemann and the birth of modern musical thought . Cambridge University Press, Cambridge 2003, ISBN 978-0-521-09636-2 .
  • Hugo Riemann (under the pseudonym Hugibert Ries): Musical logic. A contribution to the theory of music . In: New magazine for music . 39. Vol. 68, 1872, pp. 279-282 ( archive.org ).
  • Hugo Riemann: Musical logic. Main features of the physiological and psychological foundation of our music system . Leipzig 1873.
  • Hugo Riemann: Systematic modulation theory as the basis of musical form theory . Hamburg 1887.
  • Siegfried Schmalzriedt : Art. Cadence . In: Concise dictionary of musical terminology . Vol. 3, ed. by Hans Heinrich Eggebrecht and Albrecht Riethmüller , editor-in-chief Markus Bandur, Steiner, Stuttgart 1972 ( online ).
  • Elmar Seidel: Hugo Riemann's theory of harmony . In: Martin Vogel (Hrsg.): Contributions to the music theory of the 19th century . Gustav Bosse Verlag, Regensburg 1966, pp. 39–92.

Web links

Individual evidence

  1. ↑ Schmalzriedt, p. 1.
  2. ↑ Wieland Ziegenrücker: General music theory with questions and tasks for self-control. German Publishing House for Music, Leipzig 1977; Paperback edition: Wilhelm Goldmann Verlag, and Musikverlag B. Schott's Sons, Mainz 1979, ISBN 3-442-33003-3 , pp. 110–112.
  3. ↑ See Menke 2011 .
  4. ↑ Rameau 1760, p. 50: "L'enchaînement des dominantes [...] donne celui des cadences parfaites, mais généralement évitées ou simulées [...]."
  5. ↑ Wieland Ziegenrücker: General music theory with questions and tasks for self-control. German Publishing House for Music, Leipzig 1977; Paperback edition: Wilhelm Goldmann Verlag, and Musikverlag B. Schott's Sons, Mainz 1979, ISBN 3-442-33003-3 , pp. 110-114.
  6. ↑ Riemann 1872, p. 280.
  7. ↑ Riemann 1873, p. 67.
  8. ↑ Riemann 1872, p. 280. See also Seidel 1966, pp. 47-49 and Rehding 2003, pp. 68-71.
  9. ↑ Riemann 1872, pp. 281-282.
  10. ↑ Riemann 1887, p. 16.
  11. ↑ Riemann 1887, p. 16.
  12. ↑ Halm 1912, p. 28.
  13. ↑ Dachs / Söhner 1985, p. 14.
  14. ↑ Dachs / Söhner 1985, p. 25.
  15. ↑ Abraham 1965, p. 45.
  16. ↑ Dachs / Söhner 1985, p. 14: “In the cadence we encounter the first musical event. It is the model and archetype for music throughout the classical and romantic epoch. "
  17. ↑ Dachs / Söhner p. 14: “If you look closely, the cadence is divided into two parts: the first part I – IV, to which the second part V – I answers and corresponds; because both times the bass makes a fifth downward leap. [...] The same dominant relationship as with V – I also exists between I – IV. "
  18. ↑ Dachs / Söhner 1985, pp. 14-20.
  19. ↑ Abraham 1965, p. 30: “By cadence we always understand a group of chords from tonic to tonic.” See also pp. 47, 80.
  20. ↑ Abraham 1965, p. 52.
  21. ↑ Abraham 1965, pp. 43, 74, 87.